Ошибка.
Попробуйте повторить позже
Деревни некоторой языческой страны соединены дорогами так, что от любой деревни можно добраться до любой другой не проходя ни через какую деревню дважды, причём сделать это можно единственным способом. В каждой деревне живет свое племя туземцев. Каждое племя поклоняется одному из трёх идолов: Камню, Ножницам или Бумаге. Известно, что Камень сильнее Ножниц, Ножницы сильнее Бумаги, а Бумага сильнее Камня. Каждое племя желает, чтобы их идол был не слабее, чем идол любого из соседствующих с ними племен. С этой целью каждый вечер ровно в 20:24 каждое племя смотрит на своих соседей и, если обнаруживает соседа с более сильным идолом, меняет свои верования, начиная поклоняться этому более сильному идолу. Верно ли, что рано или поздно все племена начнут верить в одного и того же идола?
Источники:
Подсказка 1
Если видите в задаче ребят и дружеские связи, города, дороги и тому подобное, то сразу же переводите задачу на язык графов, так с ней намного удобнее будет работать. Обозначим города за вершины, а дороги между ними за ребра. Поверим в лучшее и попробуем доказать, что всё-таки все вершины будут иметь одного идола в конце. Подумайте над тем, какой перед нами граф и как он поможет нам в доказательстве.
Подсказка 2
В условии сказано, что существует единственный простой путь (без повторения вершин) между любыми двумя вершинами, значит, перед нами граф-дерево, а у такого графа есть «листья» (вершина, у которой есть только один «сосед»). Попробуйте доказать необходимое утверждение по индукции, рассмотрев граф на n вершин, для которого оно выполняется, а шагом индукции пусть будет добавление «листа».
Подсказка 3
Возьмем две вершины нашего графа, вершину A – лист, вершину B – родитель вершины A (единственный её «сосед»). Рассмотрите два случая, когда вершина B не меняла своего идола на идола вершины A и когда меняла. Если в каждом из случаев в графе идолы всех вершины становятся одинаковыми, то мы доказали утверждение.
Подсказка 4
Пусть B не меняла своего идола на идола вершины A, значит, либо идол B сильнее идола вершины A, либо их идолы равны. В каждом из этих случаев в один момент идолы вершин A и B будут равны, а по предположению индукции и весь граф будет иметь одинаковых идолов. Осталось аналогичным способом рассмотреть случай, когда B поменяла своего идола на идола вершины A.
Переформулируем условие задачи на язык графов. Каждому племени поставим в соответствие вершину, между любыми двумя соседними проведем ребро. Для каждой вершины определен ее идол, если идол соседней вершины сильнее, то в этот день вершина меняет своего идола на более сильного.
Будем решать задачу индукцией по количеству вершин. База индукции для графа, состоящего из одной вершины, очевидна.
Докажем, что если условие задачи верно для некоторого натурального , то оно же верно для
. Выберем висячую вершину
исходного дерева, родителем которой является вершина
.
Будем говорить, что вершина влияет на вершину
, если данные вершины являются соседями и идол
сильнее идола
, при
этом
не имеет соседа с более сильным идолом, отличным от
.
Если не существует дня, в котором вершина влияло на вершину
. В графе, полученном из данного удалением вершины A, по
предположению индукции все вершины через несколько дней будут иметь одного и того же идола, в частности его же будет иметь вершина
, а значит и вершина
.
Предположим, что существует день, в котором повлияло на
. После этого дня вершины
и
имеют одинакового идола.
Теперь, если вершина B меняет идола на более сильного, то на следующий день
так же начинает поклоняться этому идолу, а значит
не наступит дня, в котором
имело бы более сильного идола, следовательно
больше никогда не повлияет на
,
тем самым мы можем применить рассуждения, проделанные ранее, для дня, после которого вершина
повлияла на
.
Ошибка.
Попробуйте повторить позже
Есть отрезков длины
,
, …,
, где
,
, а при
выполнено
. Сколькими способами эти
отрезки можно разбить на четвёрки так, чтобы из отрезков каждой четвёрки можно было составить четырёхугольник?
Источники:
Подсказка 1
Подумайте, при каком условии из четырех отрезков можно составить четырехугольник. Вспомните аналогичное условие для треугольников.
Подсказка 2
Да, из отрезком a < b < c < d можно составить четырёхугольник <=> a+b+c > d, попробуйте рассмотреть произвольную четвёрку, которая образует четырёхугольник и расписать свойство x_k = x_{k-1} + x_{k-2} более подробно, т.е. для x_{k-1} применить его же и посмотреть чему тогда должно быть равно c и b.
Подсказка 3
Верно, если d = x_{k}, то b = x_{k-2}, c = x_{k-1}, иначе четырёхугольник не построится. Теперь задача свелась к подсчету количества способов выбрать n пар из тройки элементов и одного элемента, который не превосходит по номеру элементы выбранной тройки.
Подсказка 4
Введем понятие "хорошей" последовательности, состоящей из 2n чисел, в которой каждое из чисел 1, ..., n участвует ровно два раза. Как мы можем восстановить способ разбиения последовательности отрезков по хорошей последовательности? Может мы можем первому вхождению числа в "хорошую" последовательность сопоставить число, а второму - тройку?
Подсказка 5
Теперь давайте подсчитаем количество хороших последовательностей. Сколькими способами можно выбрать индексы для двух единиц? А сколько тогда останется возможных индексов для двух двоек? А сколько всего получится способов сопоставить каждому числу 2 индекса?
Подсказка 6
А не посчитали ли мы что-либо несколько раз? Меняет ли перестановка чисел в "хорошей" последовательности набор отрезков?
Из отрезков можно сложить четырехугольник тогда и только тогда, когда
. Рассмотрим четверку
, заметим, что
, следовательно,
, иначе проверяемое
неравенство не выполнено. Аналогично, можно показать, что
.
Назовем последовательность интересной. Таким образом, необходимо посчитать количество способов выбрать в интересной
последовательности
пар из тройки элементов и одного элемента, который не превосходит по номеру элементы выбранной
тройки.
Рассмотрим последовательность, состоящую из чисел, в котором каждое из чисел
участвуют ровно два раза и назовем ее
хорошей. Восстановим по хорошей последовательности способ разбиения интересной последовательности. На первом шаге рассмотрим первое
число в каждой из последовательности. На каждом следующем шаге, если рассматриваемое число в хорошей последовательности
встречается впервые, то ставим ему в соответствие рассматриваемое число в интересной последовательно, после чего рассматриваем
следующий числа в каждой из последовательностей. Если рассматриваемое число в хорошей последовательности встречается во второй раз,
то ставим ему в соответствие тройку из рассматриваемого элемента в интересной последовательности и двух элементов, идущих
после него. Таким образом, к концу процесса, каждому первому вхождению числа в хорошей последовательности стоит в
соответствие один элемент интересной последовательности, а каждому второму тройка подряд идущих элементов интересной
последовательности.
Посчитаем количество хороших последовательностей. Существует способов выбрать индексы двум единичкам, после этого
останется
возможных индекса, следовательно, существует ровно
способов выбрать индексы для двух двоек. Продолжая
ставить каждому из чисел в соответствие два индекса, получим что общее количество способов сделать это, равно
. Осталось
заметить, что каждая перестановка чисел в хорошей последовательности не меняет набор разбиение интересной последовательности,
следовательно, каждое разбиение было посчитано
раз (количество перестановок длины
), а значит общее количество разбиений
равно
Ошибка.
Попробуйте повторить позже
Однажды друзей, живущих в разных уголках земного шара, захотели обменяться друг с другом новостями. Для этого они собираются
устроить
видеовстреч, на каждой из которых каждый человек расскажет всем свои новости, а также все новости других людей, которые
он узнал ранее.
Для видеовстреч было предложено дней, но оказалось, что каждый из друзей может присутствовать только в какие-то
из них.
При каком наименьшем натуральном
можно гарантированно выбрать
дней для видеовстреч из предложенных
так, чтобы каждый
узнал новости каждого?
(Между предложенными днями у людей новых новостей не возникает, и никак иначе они друг с другом не общаются. В каждый из предложенных дней проходит одна видеовстреча, на которой собираются все, кто может в этот день присутствовать.)
Оценка. Приведём пример ситуации, в которой 4 дней не хватит. Пусть у каждого из 45 людей будет своя, не совпадающая с другими
людьми, пара дней, в которые он не может участвовать во встрече. Так как количество способов выбрать пару дней из 10
предложенных равно , то для любой пары дней найдётся человек, который не может присутствовать ровно в
эту пару дней. Предположим, что мы смогли выбрать какие-то 4 дня так, чтобы каждый узнал все новости. Но тогда
существует человек
, который не может присутствовать в первые два дня из этих четырёх, а также человек
, который
не может присутствовать в последние два из этих четырёх дней. Заметим, что тогда
не сможет узнать новостей
.
Противоречие.
Пример. Теперь поймём, что 5 дней всегда точно хватит. Выберем 5 дней произвольным образом. Докажем, что любые два человека будут вместе присутствовать на какой-то встрече. Действительно, среди этих 5 дней есть не более 2 дней, в которые не может присутствовать первый, а также не более 2 дней, в которые не может присутствовать второй. Значит, найдётся день, в который могут присутствовать оба человека. Таким образом, каждая пара людей сможет обменяться новостями, то есть каждый узнает новость каждого.
При
Ошибка.
Попробуйте повторить позже
Дана клетчатая доска Каждая клетка доски покрашена в один из двух цветов: белый или чёрный. Назовём раскраску доски
уравновешенной, если в каждой строке и в каждом столбце 50 белых и 50 чёрных клеток. За одну операцию разрешается выбрать две строки
и два столбца так, чтобы из 4 клеток на их пересечении две были чёрными, а две — белыми, и перекрасить каждую из этих 4 клеток в
противоположный цвет. Докажите, что из любой уравновешенной раскраски можно получить любую другую уравновешенную раскраску с
помощью указанных операций.
Источники:
Подсказка 1
Непонятно, как доказывать, что возможно перевести любую уравновешенную раскраску в любую другую. Может, тогда докажем, что любую уравновешенную раскраску можно перевести в какую-то конкретную, тогда из любой мы будем приходить в неё и уходить в любую другую, совершая в обратном порядке действия, с помощью которых мы бы приходили к ней. Надо подумать, к какой раскраске мы будем приходить...
Подсказка 2
На ум приходит, конечно же, шахматная раскраска. Но переводить доску целиком в шахматную как-то тяжеловато. Может, начать со столбцов?
Подсказка 3
Разобьем наши столбцы на пары и будем по очереди красить их в шахматную раскраску. Возьмем сейчас самую левую пару столбцов, которая еще не покрашена нужным нам образом. Будем приводить горизонтальные доминошки к шахматной раскраске сверху вниз. Что делать, если в какой-то момент у нас доминошка, которая содержит оба цвета, неправильно стоит?
Подсказка 4
Пускай для определённости левая клетка нашей доминошки черная:
Подсказка 5
А вывод такой: в какой-то доминошке, которая находится ниже нашей, левая клетка будет белой, а правая чёрной, ведь иначе суммарно чёрных клеток будет больше в первом столбце, чем во втором, а это противоречит тому, что раскраска доски уравновешенная. Тогда мы можем применить к этим двум доминошкам операцию и продолжить спуск вниз. Но что же делать, если в какой-то момент, идя вниз по столбцам, мы найдём одноцветную доминошку?
Подсказка 6
Пускай она чёрная. Можно заметить, что тогда ниже нашей доминошки существует белая доминошка (иначе в сумме по этим столбцам чёрных клеток будет слишком много). Что мы можем тогда сказать про строки, которые содержат наши доминошки?
Подсказка 7
На самом деле эти строки содержат две клетки, которые находятся в одном столбце, который находится правее наших, и при этом верхняя будет белая, а нижняя черная (Назовем этот столбец S). Это верно в силу того, что левее наших столбцов в этих строках поровну черных и белых клеток. Тогда мы можем выбрать один из наших столбцов, столбец S и поменять цвет клеток в них по этим строкам. Как же завершить решение?
Подсказка 8
Можно заметить, что, когда мы совершали операции по смене цвета, мы не нарушали уравновешенность таблицы. А это значит, что можно продолжать раскрашивать пары столбцов дальше и прийти к шахматной раскраске.
Докажем, что из любой уравновешенной доски можно получить доску, раскрашенную в шахматную раскраску, причём на каждом шаге доска будет оставаться уравновешенной. Из этого будет следовать, что из любой уравновешенной доски можно получить любую другую, так как операция обратима.
Будем получать шахматную раскраску следующим образом. Разобьём столбцы на пары подряд идущих. Выберем самую левую пару столбцов и в этой паре столбцов по очереди будем приводить строки (состоящие из двух клеток) к шахматной раскраске. После того как закончим с первой парой столбцов, перейдём ко второй и так далее.
Объясним, как делать следующий шаг внутри одной пары столбцов и
Пусть в следующей строке
сейчас находятся чёрная и
белая клетка, но в неправильном порядке. Например, слева стоит чёрная клетка, а справа белая, а должно быть наоборот.
Заметим, что во всех строках выше
в первом столбце суммарно чёрных клеток не меньше, чем во втором, так как они уже
покрашены шахматным образом. Значит, в какой-то строке
ниже
должна быть ситуация, когда в левом столбце чёрных
клеток меньше, чем в правом, т.е. должна быть строка белая-чёрная (это следует из того, что суммарно в первом столбце
столько же чёрных клеток, сколько и во втором). Произведём операцию со строками
и
и текущими столбцами.
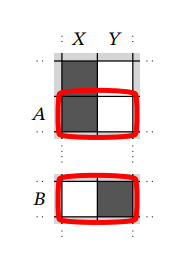
Пусть теперь у нас в строке стоят две одинаковые клетки, например чёрные. Тогда в какой-то строке
должны оказаться две
белые клетки (иначе суммарно чёрных клеток в этих двух столбцах будет слишком много). Понятно, что эта строка расположена ниже
текущей, т.к. выше неё все строки разноцветные. Теперь заметим, что если посмотреть на эту пару строк во всей таблице, то должен быть
столбец
правее
и
в котором в первой строке белая клетка, а во второй — чёрная. Тут мы пользуемся тем, что левее
наших столбцов в этих строках поровну чёрных и белых клеток. Теперь осталось лишь выбрать один из столбцов
или
(в котором неправильный цвет в строке
и столбец
а также строки
и
и произвести операцию с ними.
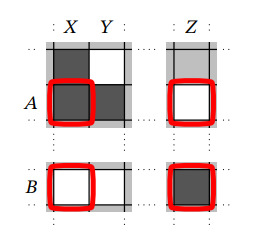
Легко видеть, что на каждом шаге уравновешенность доски сохраняется. А так как мы всегда можем сделать шаг в нашем алгоритме, то в конце получится шахматная раскраска.
Ошибка.
Попробуйте повторить позже
Каждое натуральное число покрасили в один из трёх цветов: красный, синий или зелёный, причём все 3 цвета встречаются. Может ли оказаться так, что сумма любых двух чисел разных цветов является числом оставшегося цвета?
Источники:
Подсказка 1
Если ответ да, то как доказать, что такое возможно? Привести пример раскраски... Вроде как сходу такую раскраску придумать не получается. Может тогда воспользоваться методом от противного...
Подсказка 2
Пускай такая раскраска существует. Разумно было бы посмотреть на подряд идущие числа: ведь если они разного цвета, то их разность обязана быть покрашена в оставшийся цвет. А их разность это всегда 1
Подсказка 3
Возьмем числа 1 и n такие, что их цвета не совпадают. Тогда числа 1, n и n+1 покрашены в три различных цвета. Может попробовать пойти дальше и посмотреть на n+2? Какой же цвет имеет n+2=1+(n+1)? А n+3=1+(n+2)?
Подсказка 4
Получается, что n+2 имеет цвет числа n, а n+3 имеет цвет числа n+1. Похоже, что мы больше никогда не увидим число, цвет которого совпадает с цветом числа 1:( А может ли быть такое?
Подсказка 5
Такого, конечно же, не может быть: достаточно просто посмотреть на цвет числа 2n+1=n+(n+1)
Пойдём от противного, предположим, что такое возможно. Без ограничения общности можно считать, что число 1 покрашено в красный.
Выберем произвольное число покрашенное в синий. Заметим, что тогда
должно быть зелёного цвета,
—
синего,
— зелёного и т.д. Таким образом, все числа, большие
покрашены в синий или зелёный цвет. С другой
стороны, так как
покрашен в синий цвет, a
— в зелёный, то число
должно быть покрашено в красный цвет,
противоречие. Значит, такое невозможно.
Ошибка.
Попробуйте повторить позже
Фокусник и его Ассистент готовятся показать следующий фокус. Фокуснику завяжут глаза, после чего один из зрителей напишет на доске
60-битное слово (последовательность из 60 нулей и единиц). Ассистент уверен, что сможет незаметно сообщить фокуснику 44 бита (не
обязательно написанные в слове, можно вычислять любые функции). После чего Фокусник должен будет назвать слово. Для какого
наибольшего числа Фокусник и Ассистент могут придумать стратегию, позволяющую всегда назвать слово, совпавшее хотя бы в
битах с написанным зрителем?
Источники:
Подсказка 1
Давайте начнём решать эту задачу с оценки. Причём мы будем рассуждать так, что фокусник при выписывании последовательности ошибся максимум в k символах, то есть C = 60 - k. Пусть мы знаем последовательность, написанную фокусником. Тогда с помощью какой информации на основе введённых данных мы сможем определить исходную последовательность?
Подсказка 2
Верно, нам нужно знать, в каких символах он ошибся. Тогда мы сможем однозначно определить последовательность. Но как нам это поможет в задаче? Давайте представим немного нашу задачу через множество и его покрытие. Всего возможных последовательностей, которые может написать зритель это 2^60. Давайте подумаем, как мы можем посчитать, сколько покроет одна последовательность, учитывая, что фокусник может ошибиться максимум в k знаках?
Подсказка 3
Верно, это считается с помощью числа сочетаний. Может быть такое, что он вовсе не ошибся, ошибся один раз и т.д. до максимум в k знаках. И того, для одной последовательности мы получаем сумму числа сочетаний. Но всего фокусник может получить 2^44 различных последовательностей, имея информацию от ассистента. Тогда учитывая мысль про покрытия множества размером 2^60, какую оценку мы получаем?
Подсказка 4
Да, сумма, умноженная на 2^44, должна быть больше 2^60. Но зачем? Чтобы даже, если мы ошибёмся максимум в k знаках, то мы всё равно победим, так как затронем все последовательности. Таким образом, несложной прикидкой получим оценку для k=4, откуда C=56. Теперь в следующей подсказке разберёмся с примером.
Подсказка 5
Суть нашего примера будет заключаться в том, как же действовать ассистенту, то есть какую последовательность передавать, и, что с ней делать фокуснику. Заметим, что фокусник в итоге ошибается только в 4 позициях. Давайте тогда для удобства, пока магически разобьём то, что будет передавать ассистент на блоки по 11 цифр. Тогда в каждом блоке фокусник будет что-то досчитывать, записывать и, в итоге, ошибаться максимум 1 раз в блоке. Попробуйте поугадывать, какая информация ему может понадобиться из этих 11 цифр? Стоит подумать в сторону информатики, последовательности 0 и 1 из 4 знаков и чётности, нечётности.
Подсказка 6
Давайте составим табличку из последовательностей с четырьмя символами, в которых есть хотя бы две единицы, и пронумеруем. Их будет как раз 11 штук. В последние 4 позиции блока запишем следующие "контрольные" суммы. Сначала запишем сумму по модулю два тех из первых 11 позиций, записанное 4-значное число которых имеет 1 в первом разряде. Потом аналогичное сделаем для 1 во втором разряде и т.д. до 4 разряда. Попробуем взять произвольную последовательность из 15 символов, а записать только 11. Посчитаем для них самостоятельно контрольные суммы. Теперь поизучайте эту конструкцию, например, что будет если контрольные суммы не совпадут? В скольких разрядах у них будет расхождение и где может быть ошибка – в четырех контрольных суммах или в первых 11 цифрах? А сколько в принципе может случится ошибок в такой строке, если не совпали контрольные суммы?
Подсказка 7
Ага, несложным перебором, где и сколько штук можно было допустить ошибок, понимаем, что она возможна только одна(либо в 11 цифрах, либо в контрольных суммах). Но для чего это всё таки было? Попробуйте прокрутить теперь эту конструкцию в обратном порядке. Пусть мы получили "кодовое слово" длины 15. Дальше считаем контрольные суммы по первым 11 цифрам и дописываем их. Таким образом, 15 цифр будут расходится максимум в 1 позиции. Как тогда отсюда получается окончательный пример?
Подсказка 8
Да, получается, что ассистент бьёт 60 цифр на группы по 15 и делает для них "кодовые слова" длинной 11, убирая контрольные суммы. Так и получается всего передача 44 знаков. Фокусник же далее восстанавливает контрольные суммы, как и само слово, ошибившись максимум 4 раза. Но всё таки осталось ещё понять, почему же вообще любое из слов длины 15 получается искажением какого-то из кодовых слов не более чем в одной позиции. И после этого будет победа!
Докажем оценку
______________________________________________________________________________________________________________________________________________________
Пусть существует стратегия, позволяющая ошибаться не более чем в битах
т.е.
Тогда заметим, что
Наблюдатель, знающий стратегию Фокусника, сообщенное Ассистентом слово, и набор бит, в которых ошибся Фокусник,
может восстановить написанное Зрителем слово. В самом деле, Наблюдатель берет слово, которое должен был написать
Фокусник, и меняет его в тех местах, где Фокусник ошибся. Значит, количество различных пар вида "слово сообщенное
Ассистентом и набор мест, в которых фокусник ошибся"не меньше, чем различных слов, которые мог написать зритель. То
есть
Перепишем в виде
Заметим, что при неравенство неверно:
_________________________________________________________________________________________________________________________________________________________________________________
Теперь попробуем показать, из каких соображений строится пример. Для начала напомним конструкцию, известную как математикам так и программистам: двоичный код длины 15, позволяющий передать 11 бит полезной информации и исправить ошибку не более чем в одном бите (также известен как 15-битный код Хэмминга). Построим его.
Для начала заметим, что есть ровно 11 слов длины 4 из нулей и единиц, содержащих хотя бы две единицы (всего слов минус
одно из одних нулей, минус четыре с одной единицей). Припишем такие слова номерам от 1 до 11 как угодно, например как в таблице:

Теперь построим код таким образом: в первые 11 бит запишем те биты, которые хотим передать (первые 11 позиций будем называть информационными). В последние 4 бита запишем следующие контрольные суммы. В 12-й запишем сумму по модулю два тех из первых 11 бит, приписанное 4-значное число которых имеет 1 в первом разряде, то есть биты № 3,5,6,8,9,10,11. В 13-й — сумму тех из первых 11 бит, приписанное 4-значное число которых имеет 1 во втором разряде, в 14-й сумму бит, имеющих 1 в третьем разряде приписанного слова, в 15-й — в четвертом. Покажем, почему этот код позволяет исправить одну ошибку при передаче.
_________________________________________________________________________________________________________________________________________________________________________________
Пусть Получатель получил кодовое слово, возможно искаженное в одном бите. Получатель точно так же по первым 11 битам посчитает 4 контрольные суммы, и сравнит их с четырьмя полученными. Если совпали все четыре — то слово дошло без искажений. В самом деле, если бы исказился контрольный бит — в нем было бы расхождение, а если информационный — то расхождения были бы во всех контрольных, в которые он входит. Аналогично, если расхождение есть ровно в одном контрольном бите, то исказился именно он. В самом деле, если исказился другой контрольный — то все информационные дошли правильно, тогда в этом контрольном расхождения бы не было; а если исказился информационный, то все контрольные дошли правильно, и тогда расхождения были бы во всех контрольных, в которые входит искаженный информационный, а таких контрольных хотя бы два (именно за этим мы приписывали комбинации нулей и единиц, содержащие хотя бы две единицы). По аналогичным соображениям если получатель видит не менее двух расхождений с контрольными битами, то искажен точно информационный. Тогда достаточно из 11 информационных позиций выбрать ту, в приписанном 4-битном слове которой единицы стоят ровно на тех местах, на которых есть расхождения с контрольными суммами — это и есть искаженная позиция.
_________________________________________________________________________________________________________________________________________________________________________________
Теперь подумаем в других терминах, что же мы построили. У нас есть код из кодовых слов. Каждое из этих слов можно исказить
16 способами (ничего не менять, или изменить один из 15 бит). Все
полученных в результате слов будут разными. В самом
деле, если бы какое-то слово
получалось двумя разными способами: искажением кодового слова
и искажением
кодового слова
(в обоих случаях — не более чем в одном бите), то код бы не исправлял одну ошибку — Получатель может
получить слово
но в этом случае не может понять, посылали ему
или
Итак, все
слов разные, но это
означает что вообще любое из слов длины 15 получается искажением какого-то из кодовых слов не более чем в одном
бите.
На этом и построим стратегию Фокусника и Ассистента. Ассистент видит написанное зрителем 60-битное слово, режет его на четыре
15-битных слова Как доказано выше, для них найдутся кодовые слова
такие что
отличается от
не
более чем в одном символе. Тогда Ассистент выбрасывает из каждого кодового слова контрольные символы, получает четыре слова длины
11, то есть одно слово длины 44. Его он и передает Фокуснику. Фокусник восстанавливает контрольные суммы, получает слово
отличающееся от исходного максимум в четырех битах — победа.
Ошибка.
Попробуйте повторить позже
Вася пришел в казино, имея один вшэ-коин (единственную в мире виртуальную валюту, которую можно делить на любые части; например,
можно поставить на кон вшэ-коина). В казино игрокам предлагается делать ставки на цвет шара, который будет вытащен из ящика.
Фиксировано число
причем
Если цвет вытащенного шара совпадает с тем, на который игрок поставил
денег — игрок получит назад
денег, если не совпадает — не получит ничего. Для ставок в каждом раунде можно
использовать не только деньги, имевшиеся к началу игры, но и выигрыши прошлых раундов. Перед началом игры Вася смог
подсмотреть, что в ящик положили 3 черных и 3 красных шара (других шаров нет), сыгранные шары обратно в ящик не
возвращаются, игра происходит пока ящик не опустеет. Какую максимальную сумму Вася может гарантированно иметь к концу
розыгрыша?
Источники:
Подсказка 1
Мы понимаем, что у нас в задаче Вася может максимум 6 раз сделать ставку. Тогда имеет смысл "перебрать случаи". Давайте будем заполнять табличку 4 на 4(0, 1, 2 и 3 красных шара по вертикали и аналогично для чёрных по горизонтали), которая будет говорить о том, во сколько раз увеличится выигрыш, когда осталось определённое число шаров. Тогда во сколько раз увеличатся деньги, после того как у нас останутся шары только одного цвета?
Подсказка 2
Верно, они могут увеличиваться в p, p^2, p^3 раз. Вася будет просто ставить всю сумму каждый раз на один цвет. Это то, что будет стоять в крайних столбцах и диагоналях. Ещё понятно, если шаров нет, то мы ничего не выигрываем, то есть 1 коэффициент в клетке (0; 0). Давайте поймём такую вещь, а есть ли Васе смысл ставить деньги на оба шара?
Подсказка 3
Да, смысла в этом нет, Васе надо ставить какую-то часть денег только на один цвет. Если он поставит a денег на один цвет, а b на другой, то получит на 2(p-b) денег меньше, чем если бы поставил a-b на один цвет. Это несложно посчитать. Теперь давайте попробуем разобраться с другими клетками. Например, если остался 1 чёрный и 1 красный шарик. Во сколько раз мы получим больше денег точно? Полезно будет ввести неизвестные.
Подсказка 4
Верно, мы получим больше в p раз. Дело в том, что даже если мы не угадаем шар, то следующим ходом увеличим в p раз количество денег. Давайте теперь попробуем в общем виде провести рассуждения. Если у Васи было X денег, а поставил он aX, где a какое-то число от 0 до 1. Значит, мы можем посчитать случаи, когда Вася угадал и когда не угадал. Но тогда сколько гарантированно он получит? Что это может значить с точки зрения полученных формул?
Подсказка 5
Да, гарантированный выигрыш — это минимум из двух наших выражений. Но можно заметить, что одно из них убывающее, а другое возрастающее от a. Значит, и минимум будет, когда они равны. Отсюда мы получаем a, а потом и во сколько раз увеличится наше количество денег. Так мы, постепенно заполняя таблицу, получим, что должно быть в клетке, где 3 шара каждого цвета. Это и будет ответ на задачу, победа!
Заполним табличку: в клетке запишем, на какое максимальное число Вася может гарантированно к концу игры умножить
имеющуюся у него сейчас сумму, если сейчас в ящике осталось
черных и
красных шаров. Легко понять, что стоит с краю: если уже не
осталось черных шаров, то Вася может смело ставить все деньги на красный шар, соответственно увеличивая капитал в
раз за каждый из оставшихся красных шаров. Аналогично если не осталось красных. Это и отмечено в таблице ниже.
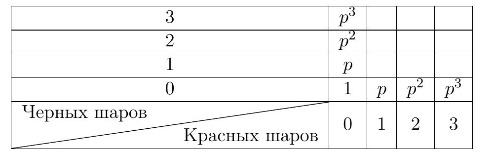
Теперь поймем, что должно стоять в клетке если мы уже знаем, что в клетках
и
стоят числа
и
соответственно. Пусть для определенности
Во-первых, в оптимальной стратегии Вася не должен делать положительные ставки на оба исхода. В самом деле, пусть по своей
стратегии он должен сейчас поставить суммы и
причем
Тогда пусть вместо этого он поставит
денег на тот исход,
на который должен был ставить
и на
больше денег оставит не поставленными. Тогда при любом исходе он будет иметь на
денег больше, чем имел бы, если бы ставил
и
Теперь поймём, сколько же Вася должен ставить. Ставить он должен на тот цвет, выпадание которого приводит в клетку с числом
напомним,
в противном случае если этот цвет выпадет, Вася не сможет увеличить свой капитал более чем в
раз, а мы строим
стратегию лучше. Для определенности обозначим количество Васиных денег через
и пусть он поставит
денег на цвет, выпадение
которого приводит в клетку с числом
Тогда если выпал этот цвет Вася оказался в этой клетке имея
денег, соответственно закончит игру, имея не менее
денег (и не может гарантированно иметь больше).
Если же выпал цвет, приводящий в клетку с числом
Вася попал туда, имея
денег, значит закончит игру,
имея не меньше
денег (и не может гарантированно иметь больше). Итак, гарантированный минимум при этой
стратегии есть
Поскольку первая из функций под минимумом возрастающая по
, а
вторая — убывающая, максимум минимума достигается при значении
для которого функции принимают одно значение.
Имеем
То есть
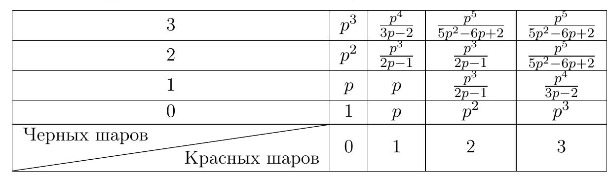
Иными словами, в интересующей нас клетке должно стоять число
Пользуясь этой формулой и значениями в клетках на краях, заполним всю табличку:
Ошибка.
Попробуйте повторить позже
Для таблички рассматриваем семейство квадратов
состоящих из клеток таблицы, и обладающее свойством: для любого
квадрата семейства найдется покрытая им клетка, не покрытая никаким другим квадратом из семейства. Через
обозначим
максимальное количество квадратов в таком семействе. Для какого наименьшего
неравенство
верно при любом
Во-первых, докажем что Для этого полезно доказать более сильное утверждение: для произвольной фигуры из
клеток
количество квадратов
в семействе, таком что все квадраты лежат в фигуре и для любого квадрата найдется клетка, покрытая только
им, не превосходит
Рассмотрим два случая: для семейства найдется клетка
покрытая четырьмя квадратами, и случай, когда
такой клетки не найдется.
Если такая клетка нашлась, то рассмотрим четыре покрывающих ее квадрата. Они образуют квадрат
с клеткой
в центре.
И поскольку в каждом из четырех квадратов
должна быть клетка, покрытая только им — это четыре угловые клетки квадрата
поскольку все остальные покрыты хотя бы дважды. Но тогда никакой другой квадрат
из семейства не покрывает
клетки квадрат
иначе он покрывает и угловую клетку, а она должна быть покрыта только один раз. Итак, все
остальные квадраты лежат в множестве площади
В этот момент доказательства еще не поздно решить, что на
самом-то деле мы ведем индукцию по
:), благо база тривиальна. Итак, всего квадратов в семействе оказывается не больше
Пусть клетки, покрытой четырьмя квадратами из семейства, не найдется. Поместим в каждую клетку множества единичный заряд.
Теперь пусть каждая клетка, покрытая квадратами из семейства, отдаст каждому из этих квадратов по
заряда (таким
образом, раздаст весь свой заряд). Тогда каждый квадрат семейства получил заряд не меньше
потому что минимум
от одной клетки получил
и от остальных получал не меньше
от каждой. Итого, всего полученного заряда не
меньше чем дважды число квадратов в семействе, а отданного заряда не больше
итого квадратов в семействе не больше
Теперь построим пример, доказывающий, что следовательно неравенство
при
неверно при всех
достаточно больших
Возьмем бесконечную клетчатую плоскость и покрасим ее в два цвета следующим образом: выберем одно из двух направлений диагонали,
покрасим все клетки каждой диагонали в один цвет: две диагонали в белый, следующие две в черный и так далее с периодом Теперь
выберем квадрат
в который черных клеток попало не меньше чем белых, то есть хотя бы
Теперь на каждую черную клетку
внутри квадрата
положим квадрат
так, чтобы кроме этой черной клетки квадрат содержал только белые (это можно сделать
единственным образом). Удалим все квадраты
частично вылезшие за границы квадрата
их не больше
Требуемое
семейство построено.
Ошибка.
Попробуйте повторить позже
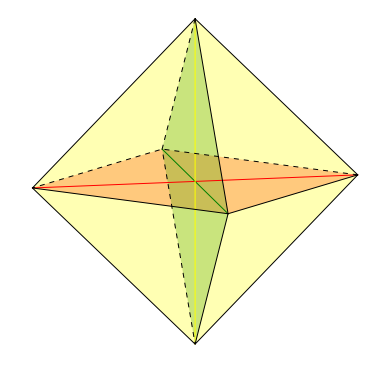
В правильном тетраэдре с ребром, равным отмечены
различных точек:
вершины и
произвольная точка внутри тетраэдра.
Никакие
отмеченные точки не лежат в одной плоскости. Докажите, что найдется тетраэдр с вершинами в отмеченных точках, объем
которого меньше единицы.
Источники:
Объем тетраэдра с ребром 8 есть поскольку этот тетраэдр получается если взять не соединенные ребром вершины куба с ребром
Заметим, что
значит если удастся тетраэдр разрезать на 64 тетраэдра с вершинами в отмеченных точках, то один из
тетраэдров разбиения будет иметь объем меньше
Докажем, что если внутри тетраэдра выбраны точек, так что если добавить к ним
вершины тетраэдра, то среди полученных
точек никакие
не лежат в одной плоскости, тогда тетраэдр можно разрезать на
тетраэдр с вершинами в выбранных
точках.
Индукция по При
считаем что тетраэдр разбит на один тетраэдр — самого себя. Пусть для
доказано, докажем для
Возьмем любые
из внутренних точек, по предположению индукции разобьем тетраэдр. Теперь добавим последнюю точку,
и посмотрим, внутрь какого тетраэдра разбиения она попала. Этот тетраэдр разобьем на четыре, каждый из которых
образован новой точкой и гранью разбиваемого тетраэдра. Разбитый тетраэдр заменим в разбиении четырьмя новыми, число
тетраэдров в разбиении выросло на
(
добавили
убрали). Итак, при
имеем разбиение на
тетраэдра, что и
требовалось.
Ошибка.
Попробуйте повторить позже
В пространстве даны точек, таких что в проекциях на координатные плоскости никакие три точки не лежат на одной прямой. Могло ли
оказаться так, что каждая точка ровно в одной из этих проекций лежит внутри выпуклой оболочки остальных? (Мы говорим, что точка
лежит внутри выпуклой оболочки других точек, если она лежит внутри треугольника с вершинами в некоторых трёх из этих
точек.)
Источники:
У нас есть координаты. По каждой координате можно выбрать точку, у которой эта координата максимальная и точку, у
которой эта координата минимальная. Таким образом, мы
раз выбираем какую-то точку. Значит какую-то точку мы
выберем
раза. Не умаляя общности, пусть у этой точки максимальная координата
и
. Тогда при любой проекции
какая-то координата у нее будет оставаться максимальной, поэтому она не может лежать в какой-то выпуклой оболочки при
проекции.
нет
Ошибка.
Попробуйте повторить позже
Каждый член партии доверяет пяти однопартийцам, но никакие двое не доверяют друг другу. При каком минимальном размере партии такое возможно?
Будем представлять партию в виде ориентированного графа: партийцев — в виде вершин, а если партиец доверяет партийцу
то
соединим вершину
с
ребром со стрелкой, направленной от
к
Условие того, что никакие два партийца не доверяют друг другу,
эквивалентно условию того, что никакие две вершины не соединены двумя противоположно направленными ориентированными рёбрами.
Будем называть это условием одного ребра.
Построим пример партии из человек, удовлетворяющей условию задачи. Разместим
человек в вершинах правильного
-угольника
Для каждой вершины
направим по ориентированному ребру из неё в каждую из пяти вершин, следующих за
ней по часовой стрелке. Утверждается, что условие одного ребра выполнено. Действительно, для каждого ориентированного ребра, идущего
от некоторой вершины
к
имеется не более
вершин, следующих от
к
в направлении по часовой стрелке. А
остальных вершин
-угольника, отличных от
и вышеупомянутых последовательных вершин между ними не
меньше, чем
и они идут последовательно от
к
по часовой стрелке «с другой стороны». Предположим
противное: условие одного ребра не выполнено, то есть некоторая пара вершин
и
соединена двумя противоположно
направленными рёбрами. Тогда в силу предыдущего, имеется два набора последовательных вершин, каждый из не более, чем 4
вершин: вершины одного набора идут от
к
по часовой стрелке, а вершины другого — от
к
по часовой
стрелке. Следовательно, эти наборы не пересекаются, и вместе с вершинами
и
(итого не более, чем
вершин) они покрывают все
вершин
-угольника. Полученное противоречие доказывает, что условие одного ребра
выполнено.
Докажем теперь, что для партии меньшего размера это не возможно. Пусть — общее число членов партии, удовлетворяющей
условиям задачи. Тогда общее число ориентированных рёбер равно
по
рёбер, исходящих из каждой вершины. С другой стороны,
общее число рёбер не превосходит множества пар различных вершин (условие одного ребра), которое, в свою очередь, равно
Тем самым,
а, значит,
то есть
Ошибка.
Попробуйте повторить позже
В компании из человек некоторые компаниями по трое ходили вместе в походы. Верно ли, что среди них найдутся четверо, среди
которых каждые трое ходили вместе в поход, либо четверо, где никакие трое не ходили вместе в поход?
Источники:
Подсказка 1
Очень часто в задачках на графы мы "зарисовываем" условие в виде графа с вершинами и рёбрами. Однако тут речь идёт о тройках, а не парах, так что соединять рёбрами не очень удобно. Может, попробовать представить граф немного в другом виде?
Подсказка 2
Конечно, можем изобразить всё в виде октаэдра, каждой вершине которого соответствует человек. Тогда группе из трёх человек соответствует либо грань фигуры, либо плоскость, проходящая внутри октаэдра и соединяющая 4 вершины.
Подсказка 3
Если не совсем понятно, что дальше делать, можно начать рассматривать различные способы выбора таких плоскостей. Попробуйте подтвердить или опровергнуть предположение из условия (помните, что для опровержения достаточно лишь одного контрпримера, так что попробуйте начать составлять именно его)
Рассмотрим октаэдр. Пусть каждый человек соответствует вершине октаэдра.
В качестве троек, ходивших вместе в поход, возьмём грани, а также ещё получаемых следующим образом. Рассмотрим три
координатных плоскости. Каждая из них пересекает октаэдр по квадрату (закрашены разными цветами). В каждом таком квадрате возьмём
две тройки, чтобы полученные треугольники вместе образовывали квадрат, и три прямых, разделяющих треугольники в парах, лежали на
трёх различных координатных прямых. (Отрезки, разделяющие треугольники, в квадратах проведены соответствующими цветами.) Легко
видеть, что такой набор троек не удовлетворяет условию задачи.
Нет
Ошибка.
Попробуйте повторить позже
В классе учеников. Их нужно разбить на две группы (первую и вторую), состоящие из чётного числа учеников. Сколькими способами
это можно сделать?
Если в первой группе человек,
то количество способов разбиения учеников в этом случае равно
(выбрали
человек
в одну группу, остальных — во вторую). Значит, чтобы получить ответ, нужно просуммировать полученную цешку при
Ошибка.
Попробуйте повторить позже
Во время матча “ЦСКА” - “Реал” пришедший с шахматного кружка Незнайка задумался: при каком наибольшем на шахматное поле
можно поставить
коней,
королей и
футбольный мяч (занимает одну клетку, но бить не умеет) так, чтобы не было фигуры,
стоящей под боем другой фигуры? Помогите ему решить эту задачу.
Источники:
Подсказка 1
В задачах на ходы необычных фигур полезно бывает выделить области, в которых мы точно сможем оценить количество фигур. Какие несложные фигуры для разбиения можно выбрать?
Подсказка 2
На квадраты 2*2! Сколько королей и коней можно поставить в каждую из них? Квадраты с королями рассмотреть несложно, а о расположении коней нужно подумать. Какое их взаимное расположение внутри квадрата допустимо?
Подсказка 3
Заметим, что кони и короли стоят в разных квадратах, а случай двух коней у границы отданного квадрата требует отдельного рассмотрения. Осталось лишь точно оценить количество коней в квадратах и построить пример!
Предположим, что на поле можно разместить фигуры при , тогда можно разместить и при
. Разобьём поле на 16 квадратов
, тогда ровно в 12 из них будут стоять по 1 королю («к»), а в 4 других - 12 коней-лошадей («л») и 1 мяч, т.е. 13 фигур, значит, пустых
квадратов быть не должно. Соответственно, квадраты будем называть к-квадраты и л-квадраты. Заметим, что если хотя бы в одном
из л-квадратов две «л» стоят у общей стороны с другим квадратом, то этот соседний квадрат не будет содержать «к»,
значит, он должен быть л-квадратом, но тогда в сумме в этих двух квадратах разместится не более 4 фигур, т.к. клетки
прямоугольника
разбиваются на пары в виде хода «л», а во всех 4 л-квадратах разместится не более
фигур, а должно быть 13. Кроме того, не существует л-квадратов с 4 «л» (аналогичные рассуждения). Значит, в каждом
л-квадрате будет ровно 3 «л» и никакие 2 «л» не могут стоять парой у общей стороны с другим квадратом, следовательно,
такие л-квадраты находятся в углах поля
и 3 «л» стоят с краю всего поля, причём в одном из них ещё стоит и
мяч.
![]()
Тогда из двух выделенных на поле квадратов хотя бы один должен оказаться пустым противоречие. Значит, .
Для уже можно построить пример. Отметим слоном мяч и поставим королей и коней.
![]()



