Ошибка.
Попробуйте повторить позже
Основанием четырехугольной пирамиды является параллелограмм
со сторонами
и углом
,
равным
. Высотой пирамиды
является отрезок
, где
- точка пересечения диагоналей параллелограмма
. Найдите площадь сечения пирамиды
плоскостью, параллельной медиане
боковой грани
и
проходящей через середину ребра
и середину отрезка
.
Пусть — середина ребра
а точка
- середина отрезка
. Рассмотрим плоскость
. Так как плоскость сечения
параллельна медиане
и проходит через точку
, построим прямую
в плоскости
. Тогда
- средняя линия в
, а
середина
.
Теперь нам известны три точки сечения: . Рассмотрим основание пирамиды
и посмотрим, как прямая
пересекает
стороны основания. Пусть эта прямая пересекает прямые
в точках
.
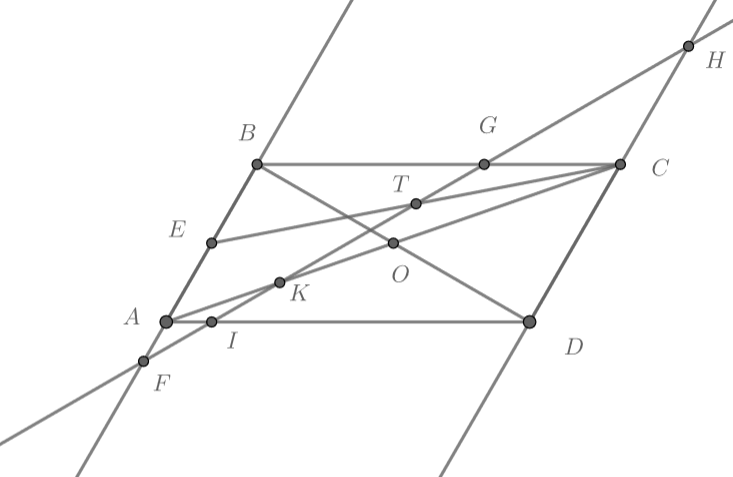
Из теоремы Менелая для треугольника получаем, что
Так как , то
.
Далее замечаем, что . Тогда
Откуда .
Из подобия получаем
То есть .
Аналогично из подобия получаем
То есть .
Проведем , где
- точка на
. Тогда
И . Тогда из теоремы косинусов для треугольника
получим
.
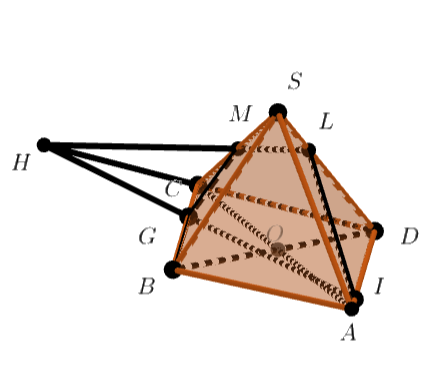
Пусть - точка, в которой прямая
пересекает ребро
. Тогда из теоремы Менелая для
и прямой
получим:
Далее из теоремы Менелая для имеем:
В силу параллельности прямых и
имеем
, откуда
. По теореме косинусов для
имеем
, то есть
. Из теоремы Пифагора для треугольника
получаем
, откуда
. По теореме косинусов для
имеем
, а значит
. По теореме Пифагора для
вычислим
. Заметим, что для треугольника
выполняется теорема Пифагора, то есть угол
прямой.
С помощью теоремы косинусов для треугольника
вычислим
. Теперь через теоремы косинусов
для треугольников
и
вычислим длины отрезков
. Далее по теореме Герона получаем
.
Заметим, что . Значит,
.
Ошибка.
Попробуйте повторить позже
В основании призмы лежит равносторонний треугольник площади 1. Площади её боковых граней равны 3, 3 и 2. Найдите объём призмы.
Источники:
Подсказка 1
Во-первых, надо осознать картинку. Она, как будто, симметричная, но не стоит так думать сразу. Давайте опустим высоты из точки A_1 на прямые AB, AC, и плоскость ABC. Что тогда можно заметить? Какие принципиально разные случаи есть падения высоты на плоскость ABC?
Подсказка 2
Есть два случая - падение во внутрь призмы и во вне. Однако, при всем этом, у нас расстояния от точки A_1’(основание высоты) до прямых AB и AC равны, в силу равенства прямоугольных треугольников. Как тогда можно равносильно переформулировать случаи, когда высота падает во внутрь, а когда наружу? Как связать это с равноудаленностью от сторон?
Подсказка 3
Все верно, либо точка основания высоты лежит на внешней биссектрисе, либо на внутренней(угла BAC). Давайте посмотрим на второй случай. Мы видим, что прямые AA’ и A_1A’ перпендикулярны BC. Что тогда это значит? Чем это хорошо в нашей картинке?
Подсказка 4
Тем, что тогда BB_1 перпендикулярен BC, а значит BB_1C_1C - прямоугольник. Но тогда, если сторона треугольника в основании равна а, выходит, что a * AA_1 = 2, a * A_1K = 3. Тогда, пришли к противоречию, так как A_1K > AA_1. Значит, остался второй случай. Если прямая внутренней биссектрисы, была перпендикулярна прямой BC, то внешняя биссектриса будет…
Подсказка 5
Параллельна! А тогда, высота в параллелограмме CC_1B_1B - высота призмы. Значит, остается найти C_1H. Ну, а это уже чисто дело техники(и нескольких теорем Пифагора).
Если бы призма была прямая, то площади боковых граней были бы равны. Значит, призма наклонная.
Обозначим призму площади из условия
Пусть — высоты параллелограммов
и
Тогда
т.к. площади равны, а также равны их
основания, так как равносторонний треугольник.
Пусть — проекция
на плоскость
Тогда
следовательно, точка равноудалена от прямых
и
(a) Рассмотрим случай, когда принадлежит биссектрисе
угла
— высота, медиана и биссектриса в равностороннем
треугольнике.
![]()
Тогда получаем, что — прямоугольник. Пусть сторона треугольника
равна
Посчитаем площадь прямоугольника и
параллелограмма.
Но тогда
(b) Рассмотрим случай, когда принадлежит внешней биссектрисе
угла
![]()
Но следовательно,
откуда следует, что высота
параллелограмма
совпадает с
высотой призмы
В итоге
Ошибка.
Попробуйте повторить позже
Ортогональной проекцией правильной треугольной пирамиды на некоторую плоскость является параллелограмм с острым углом .
Найдите объём пирамиды, если площадь её боковой поверхности равна 54.
Источники:
Пусть сторона основания пирамиды с вершиной
равна
, а боковое ребро равно
. Для построения проекции достаточно
рассмотреть две пары скрещивающихся ребер, например
и
, проекции которых являются сторонами параллелограмма
![]()
Пусть — общий перпендикуляр пары рёбер
и
, а
— общий перпендикуляр скрещивающихся рёбер
и
.
Плоскость проекции
параллельна как
, так и
, поскольку ортогональной проекцией пирамиды является параллелограмм.
Отрезки
и
проектируются на плоскость
без изменения длины в высоты параллелограмма
и
, так как
и
обе перпендикулярны
и будут параллельны друг другу, т.к.
— параллелограмм. То есть
не просто общий
перпендикуляр
и
, но и общий перпендикуляр двух вышеописанных плоскостей. А значит ещё это и общий перпендикуляр для
и
Поскольку пирамида правильная, . Следовательно,
![]()
В параллелограмме высоты, проведённые к смежным сторонам, равны — значит, параллелограмм является
ромбом.
Пусть ребро наклонено к плоскости
под углом
, тогда ребро
, которое перпендикулярно
, наклонено под углом
. Отсюда
Обозначим . Тогда
.
Найдём расстояние между скрещивающимися рёбрами правильной треугольной пирамиды как высоту сечения :
откуда
Тогда синус острого угла пирамиды равен . Подставляя найденные выражения и данное в условии значение
, получим
, откуда
(что невозможно) или
Площадь боковой поверхности пирамиды равна
Подставив и
, найдём
Объём правильной пирамиды равен
Ошибка.
Попробуйте повторить позже
Боковые рёбра треугольной пирамиды попарно перпендикулярны, а стороны основания равны ,
,
. Центр сферы, которая
касается всех боковых граней, лежит на основании пирамиды. Найдите радиус этой сферы.
Источники:
Подсказка 1
Для начала, можно найти оставшиеся длины ребер: у нас же они перпендикулярны, а значит, можно применить теорему Пифагора!
Подсказка 2
С длинами разобрались, а что делать с радиусом вписанной сферы? На плоскости у нас есть полезный факт, что r = S/p, где S - площадь треугольника, а p - полупериметр. Если вы помните доказательство этого факта, то проведите аналогичные рассуждения здесь)
Подсказка 3
Если не помните, то сделайте вот что: вот у нас есть центр сферы O. Проведем отрезки из O ко всем вершинам пирамиды. Тогда он разбивается на 3 маленьких тетраэдра. Тогда его объем - сумма объемов маленьких тетраэдров. А чему равны объемы маленьких тетраэдров?)
Подсказка 4
А они равны 1/3 × r × (площадь грани). Причем площадь грани очень легко посчитать т.к. боковые ребра - перпендикулярны, и их длины мы знаем! Осталось ещё вспомнить формулу объема пирамиды у которой боковые ребра перпендикулярны, и дело в шляпе!
![]()
Обозначим основание пирамиды — , вершину пирамиды —
, центр сферы —
, радиус сферы —
. Пусть
. Обозначим
.
Так как радиус, проведённый в точку касания сферы и плоскости, ортогонален плоскости, имеем:
С другой стороны, так как боковые рёбра попарно перпендикулярны, то
Поэтому
Числа находятся из системы уравнений:
Складывая уравнения системы и деля на два, получим:
откуда . Тогда
Ошибка.
Попробуйте повторить позже
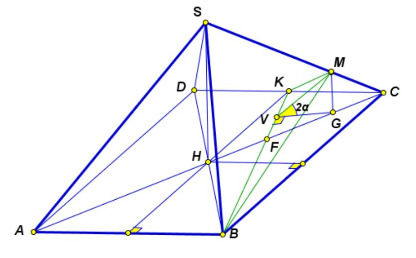
Найдите площадь сечения правильной шестиугольной пирамиды плоскостью, проходящей через вершину
основания
и параллельной медиане
боковой грани
и апофеме
боковой грани
если сторона основания пирамиды
равна
а расстояние от вершины
до секущей плоскости равно
Источники:
Построим сечение пирамиды. В плоскости через точку
проведем прямую
параллельную
принадлежит прямой
Тогда
будет средней линией треугольника
следовательно,
где
— сторона основания
пирамиды.
Плоскость содержит прямые
и
которые параллельны плоскости сечения, следовательно, по признаку плоскость
параллельна плоскости сечения.
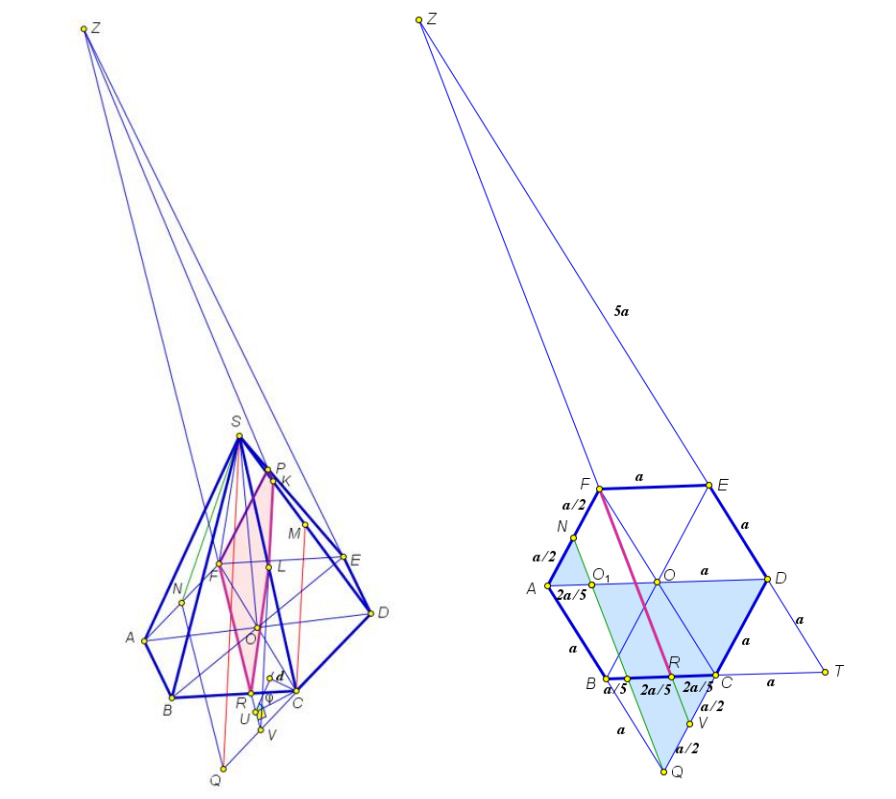
Через точку проведем прямую
параллельную
где
принадлежит прямой
Т.к.
и
значит,
— параллелограмм, следовательно,
Учитывая, что
— середина
а также
можем
сказать, что
Пусть — точка пересечения прямых
и
Плоскость сечения пересекает основание пирамиды по отрезку
Пусть — точка пересечения
и
Заметим, что углы
И
равны как вертикальные, а углы
и
как накрестлежащие при параллельных прямых
и
и секущей
Следовательно, треугольники
и
подобны,
поэтому
Т.к. является правильным шестиугольником, значит,
Учитывая, что
получаем,
что
Т.к.
и
углы
и
равны, аналогично, т.к.
и
углы
и
равны, а также
следовательно, треугольники
и
равны, поэтому
Пусть точка — точка пересечения прямых
и
а точка
— точка пересечения прямых
и
Из-за того, что
— правильный шестиугольник, можно сделать вывод, что
Т.к.
треугольники
и
подобны, поэтому
В плоскости через точку
проведем прямую
параллельную
принадлежит ребру
— точка пересечения
прямой
с ребром
параллельны друг другу, поэтому по теореме Фалеса имеем
В плоскости точка
— точка пересечения прямых
и
Запишем теорему Менелая для треугольника
и секущей
Искомое сечение - это Для нахождения площади сечения используем формулу
где — площадь проекции сечения на плоскость основания,
— угол между плоскостью сечения и плоскостью основания. Найдем
площадь проекции сечения на плоскость основания.
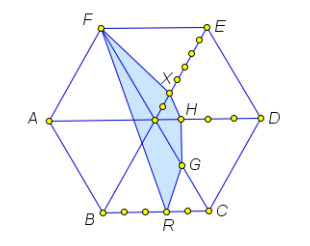
Проекцией является пятиугольник Площадь проекции сечения вычисляется по формуле
Обозначим расстояние от точки до плоскости сечения
Т.к. точка
принадлежащая плоскости сечения является
серединой
расстояние от точки
до сечения тоже равно
В треугольнике
проведем высоту
обозначим ее длину
Тогда
Т.к. — правильный,
Тогда найдем
по теореме косинусов:
Используя различные формулы для нахождения площади треугольника имеем
Тогда
Окончательно имеем
Ошибка.
Попробуйте повторить позже
На ребре основания треугольной пирамиды
расположена точка
так, что
. Через середину ребра
основания пирамиды проведена плоскость
, проходящая через точку
и параллельная боковому ребру
. В каком отношении
плоскость
делит объем пирамиды?
Источники:
Подсказка 1
Давайте для начала построим сечение плоскостью P нашей пирамиды.
Подсказка 2
Пользуясь параллельностью, мы сможем из подобия найти, в каком отношении плоскость P делит рёбра пирамиды, а значит мы сможем найти и...
Подсказка 3
Как относятся высоты маленьких пирамидок и высотам из точек A и D пирамиды ABCD.
Подсказка 4
Нам достаточно найти, какую часть объёма всей пирамиды ABCD составляет объём многогранника, лежащего со стороны вершины A. Чтобы найти его объём, можно...
Подсказка 5
Разбить его на две пирамидки. А объём каждой из них мы сможем выразить через объём всей пирамиды ABCD, потому что знаем отношения высот и отношения площадей оснований.
Построим сечение. Поскольку секущая плоскость параллельна ребру , она пересечет плоскость
по прямой
, параллельной
, а плоскость
— по прямой
, также параллельной
. Соединим точки
и
, лежащие в одной плоскости, и точки
и
, лежащие в одной плоскости, получим
— искомое сечение.
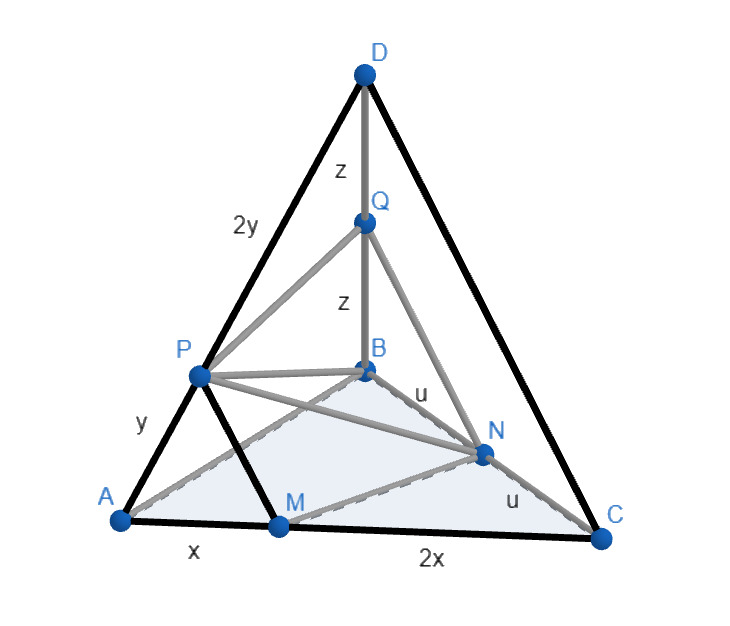
Пусть — объем пирамиды,
— сумма объемов пирамид
и
и
.
Из подобия пар треугольников и
и из условия задачи получим, что
Отсюда следует, что
где — высота, опущенная из вершины
пирамиды
,
— высота, опушенная из вершины
пирамиды
.
А также значит, что площадь основания пирамиды равна:
Тем самым:
Аналогично из подобия пар треугольников и
и из условия задачи получим, что
Отсюда следует, что
где — высота, опущенная из вершины
пирамиды
,
— высота, опущенная из вершины
пирамиды
.
А также значит, что площадь основания пирамиды равна:
Тем самым:
Теперь можно записать, что
Ошибка.
Попробуйте повторить позже
Через середину бокового ребра правильной треугольной пирамиды проведено сечение, параллельное двум скрещивающимся ребрам этой
пирамиды. Найдите площадь этого сечения, если сторона основания равна , а боковое ребро равно
Пусть — правильная пирамида, а сечение проходит через середину
. В силу симметрии можно утверждать, что оно параллельно
и
. Итак,
— середина
,
— плоскость сечения, тогда в силу её параллельности
выполнено
, где
—
середина
. Далее, если
— высота основания, а
— её середина, то
, поскольку в силу параллельности
в
лежит
вся средняя линия
(
) треугольника
. Осталось снова воспользоваться
, откуда вся средняя линия
(
) треугольника
лежит в
, то есть
— сечение (построение сечения стандартно, как на ЕГЭ, но требует
обоснований).
Итак, , а также
как средние линии, следовательно,
— параллелограмм,
— его высота,
, так что
.
![]()
Ошибка.
Попробуйте повторить позже
и
– проекции вершины
правильной треугольной пирамиды
на биссекторные плоскости двугранных углов при рёбрах
и
Найдите тангенс каждого из этих углов, если объём пирамиды
в
раз меньше объёма пирамиды
Источники:
![]()
Точки и
симметричные S относительно биссекторных плоскостей, лежат в плоскости
А поскольку тройка этих
биссекторных плоскостей переходит в себя при повороте на
вокруг оси пирамиды, то этим свойством обладает и тройка точек
Следовательно, треугольник
–правильный, и его центр, который мы обозначим через
совпадает с центром
треугольника
Заметим, далее, что пирамида – образ пирамиды
при гомотетии с центром
и коэффициентом
С учётом
условия задачи это означает, что отношение объёмов пирамид
и
равно
А поскольку у этих пирамид общая
высота
то и отношение площади треугольника
к площади треугольника
равно
В качестве следствия
получается равенство
которое будет нами использовано.
Обозначив величину двугранного ребра при ребре через
, точкой, симметричной
относительно соответствующей биссекторной
плоскости будем считать
Тогда
где
-– середина ребра
; треугольник
– равнобедренный
откуда
А поскольку
то
При левая часть последнего равенства равна
что позволяет найти
Ошибка.
Попробуйте повторить позже
Плоскость, параллельная основанию пирамиды
, отсекает пирамиду
(вершины
расположены на
рёбрах
соответственно). Объём пирамиды
равен 375 , объём пирамиды
равен 81. Найдите объём
пирамиды
.
Источники:
Подсказка 1
Т.к. плоскости (A₁B₁C₁) и (ABC) параллельны, то MA₁/MA=MB₁/MB=MC₁/MC=k. Тогда объемы тетраэдров MA₁B₁C₁ и MABC относятся как коэффициент подобия k в кубе. Чему же равен k?
Подсказка 2
Верно, 3/5! Мы видим, что объем тетраэдра MAB₁C₁ состоит из объемов тетраэдров MA₁B₁C₁ и AA₁B₁C₁, у которых есть общее основание. Как же тогда относятся их объемы...
Подсказка 3
Они относятся как высоты, которые, в свою очередь, относятся как MA₁/A₁A=3/2. Посчитайте объем AA₁B₁C₁ и завершите решение!
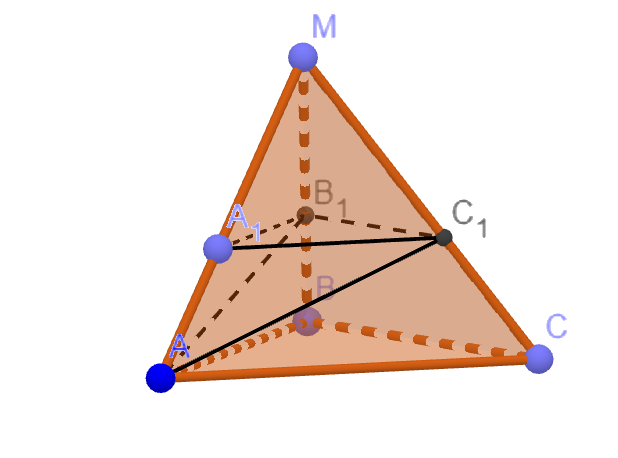
Так как плоскость параллельна плоскости основания
то
Пирамиды и
подобны, тогда их объёмы относятся как коэффициент подобия
в кубе:
Пусть тогда
Заметим, что объём пирамиды
складывается из двух кусочков:
объём
которой мы знаем, и
Причём эти 2 пирамиды имеют общее основание
тогда их объёмы относятся так же, как
относятся их высоты к
А высоты относятся так же, как относятся
и
то есть высота пирамиды
больше
высоты пирамиды
в
Значит,
Ошибка.
Попробуйте повторить позже
Дана четырёхугольная пирамида в основании которой лежит параллелограмм
Плоскость
пересекает рёбра
и
пирамиды в точках
и
соответственно. Известно, что
Найдите
Источники:
Подсказка 1
У нас уже есть три отношения, но очень хочется заполучить еще и четвертое... Давайте попробуем найти t = OD'/OD. Для этого введем систему координат с центром O и базисными векторами OA, OB и OC. Какие координаты имеют наши точки в этой системе?
Подсказка 2
Очевидно, что A (1, 0. 0), B (0, 1, 0) и C (0, 0, 1). Значит A' (1/a, 0, 0), B' (0, 1/b, 0), C' (0, 0, 1/c). Т.к. ABCD- параллелограмм, то вектор CD = BA = OA-OB. Чему тогда равен вектор OD?
Подсказка 3
Верно, OA-OB+OC! Тогда D (1, -1, 1) ⇒ D' (t, -t, t). Можно заметить, что плоскость α задается в нашей системе координат уравнением ax + by + cz = 1. Поэтому верно равенство at - bt + ct = 1 (Просто подставили точку D' в это уравнение). Итого, t = 1/(a - b + c). А что мы вообще хотели...
Подсказка 4
Нам нужно найти отношение объемов. Мы умеем легко это делать для тетраэдров, поэтому предлагаю разбить нашу пирамиду OA'B'C'D' на два тетраэдра OA'B'C' и OA'C'D'. Тогда V(OA'B'C'D')/V(OABCD) = V(OA'B'C')/V(OABCD) + V(OA'C'D')/V(OABCD). Т.к. ABCD- параллелограмм, то V(OABCD) = 2V(OABC) = 2V(OACD). А чему равно отношения V(OA'B'C')/V(OABC) и V(OA'C'D')/V(OACD)?
Подсказка 5
Т.к. тетраэдры с общим трехгранным углом относятся так же, как произведение отношений соответствующих сторон, то V(OA'B'C')/V(OABC) = 1/abc. Найдите оставшееся отношение и завершите решение!
Отношение объём пирамид с общим трёхгранным углом равно произведению отношений длин рёбер, исходящих из этого угла,
где Поскольку треугольники
и
равны,
Значит,
Дальше можно было бы строить сечение и использовать для подсчёта отношений теоремы Фалеса и Менелая, но мы воспользуемся координатно-векторным методом.
— параллелограмм, поэтому
и, следовательно,
Если точка принадлежит плоскости
а
коэффициенты
и
удовлетворяют уравнению
(это, как известно, уравнение плоскости, даже если система координат не декартова, а точки
и
этому
уравнению, очевидно, удовлетворяют).
Получаем
Обратная величина является ответом к задаче.
Ошибка.
Попробуйте повторить позже
Шар радиуса лежит внутри правильной четырехугольной пирамиды
со стороной основания 8 и высотой 3.
Этот шар касается плоскости основания
пирамиды и боковых граней
и
Плоскость
касается
шара, проходит через точку
середину
ребра
и пересекает ребро
в точке
Найдите объем пирамиды
Поскольку пирамида правильная, то центр
указанного шара лежит в плоскости
, где
— высота пирамиды. Пусть
Обозначим Проведем
— точка касания шара плоскости
пусть радиус шара
Поскольку
то
Треугольники
и
подобны, и
или
По условию задачи Тогда
Точка — точка пересечения
и
тогда
Поскольку
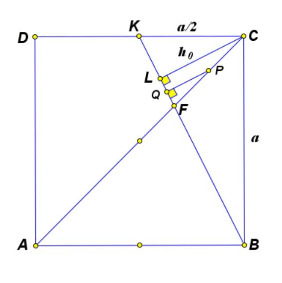
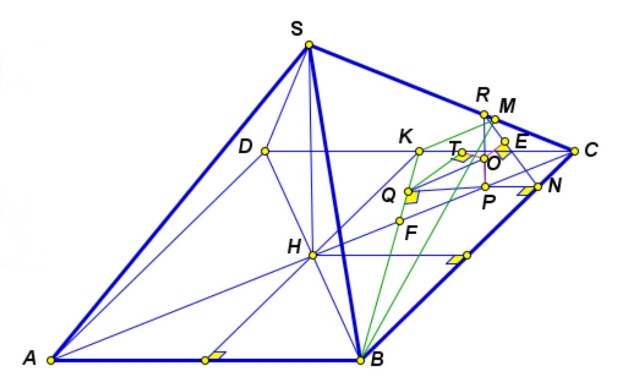
Пусть . Тогда
Если
то
Угол между плоскостью
и плоскостью основания
равен
Тогда
Пусть — отрезок перпендикуляра, опущенного из точки
на плоскость основания
, и
. Тогда
. Если
, то
— высота треугольника
проведенная из вершины
Ошибка.
Попробуйте повторить позже
Звездолёт находится в полупространстве на расстоянии от его границы. Экипаж знает об этом, но не представляет, в каком направлении
двигаться, чтобы достигнуть граничной плоскости. Звездолёт может лететь в пространстве по любой траектории, измеряя длину
пройденного пути, и имеет датчик, подающий сигнал, когда граница достигнута. Может ли звездолёт гарантированно достигнуть границы,
преодолев путь длиной не более
Источники:
Подсказка 1
В условии сказано, что пройдя расстояние, равное a, в определенную сторону, звездолет покинет полупространство. Каким образом мы можем описать все варианты той точки, где кончается полупространство?
Подсказка 2
Мы можем сказать, что если звездолет находится в какой-нибудь точке О, то на сфере с центром в точке O и радиусом a гарантированно найдется точка , которая уже не будет являться частью полупространства. Подумайте, как данная сфера может помочь в выборе траектории. Может быть, есть какая-то фигура, которую удобно будет описать около сферы?
Подсказка 3
Рассмотрите правильный октаэдр, описанный около данной сферы. Если мы докажем, что путь из центра октаэдра по всем вершинам без повторений меньше 14a и хотя бы одна вершина гарантировано не лежит в полупространстве, то мы решим задачу. Сначала подумайте, как можно сделать второе.
Подсказка 4
Воспользуемся методом от противного. Подумайте, где возникает противоречие, если мы скажем, что все вершины октаэдра лежат в данном полупространстве.
Подсказка 5
Теперь нужно найти длину пути от О и по всем вершинам. Давайте назовем наш октаэдр A₁A₂A₃A₄A₅A₆, тогда не трудно найти кратчайший маршрут обхода: O -> A₁ -> A₂ -> A₃ -> A₄ -> A₅ -> A₆. Как можно найти длину данного пути?
Подсказка 6
Для начала нужно найти длину отрезка OA₁, так как из него легко можно выразить длину ребра октаэдра. Мы знаем, что длина высоты, опущенной из точки О на грань октаэдра равна a, Тогда как мы можем найти длину OA₁?
Подсказка 7
Давайте рассмотрим пирамиду OA₁A₂A₃, найдем ее объем двумя разными способами, как 1/6 куба с ребром OA₁ и через длину высоты и площадь A₁A₂A₃. Из равенства двух данных выражений легко можно выразить OA₁. Для окончательного решения останется только найти длину ребра и доказать, что предложенный нами маршрут меньше 14a.
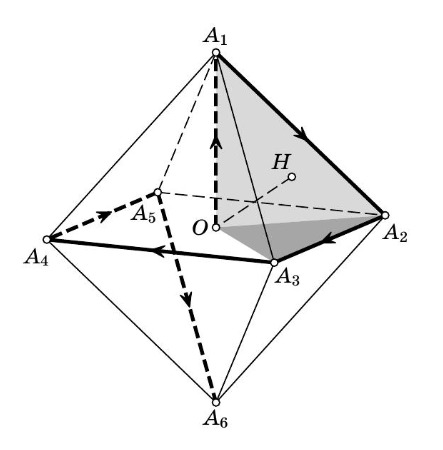
Пусть корабль находится в некоторой точке Рассмотрим правильный октаэдр
описанный возле шара радиуса
с
центром в точке
Докажем, что путь
заведомо позволит достигнуть граничной
плоскости.
Предположим противное. Тогда вершины октаэдра, а значит, и сам октаэдр (выпуклая оболочка его вершин) лежат
строго внутри полупространства. Поэтому вписанный шар октаэдра, радиус которого равен тоже лежит строго внутри
полупространства. Получаем противоречие, так как по условию расстояние до граничной плоскости полупространства равно
Покажем теперь, что длина пути меньше
Пусть
— высота
пирамиды
Запишем ее объём двумя способами:
Отсюда получаем, что а длина ребра октаэдра равна
Поэтому длина пути равна
так как
Ошибка.
Попробуйте повторить позже
В треугольной пирамиде в основании лежит равнобедренный прямоугольный треугольник
с гипотенузой
Боковые
грани
и
перпендикулярны плоскости
Сфера радиусом, равным
с центром в точке
делит пирамиду на две
части. Найдите объём большей из этих частей, если
Источники:
Подсказка 1
Из условия сразу можно понять, что SA перпендикулярно плоскости ABC. Работать просто так с пирамидой не очень удобно, к тому же у нас ещё присутствует сфера в задаче. Видим, что у нас прямой угол в основании и прямой угол между ребром и основанием! Тогда до чего можно достроить нашу пирамиду?
Подсказка 2
Верно, можно сначала отразить симметрично пирамиду относительно AC. А дальше понятно, что это большая пирамида будет 1/3 от куба, до которого тоже в силу равенства отрезков можно достроить. Но хватит ли этого нам? У нас есть сфера, которая отсекает от исходной пирамиды часть, и не совсем понятно, как вообще этот объём искать... Как можно задействовать неиспользуемую часть, после чего всё станет намного проще?
Подсказка 3
Да, можно наш куб со стороной равной двум достроить ещё до куба со стороной 4. Теперь какой же объём нас интересует?
Подсказка 4
Верно, нам нужен объём, который получается, как разность объёма сферы и 6 сегментов, выходящих наружу за куб. А точнее, потом нам нужно поделить его на 48. Отлично! Осталось аккуратно посчитать эти объёмы, и потом ещё проверить, что вы нашли больший из них. Например, можно проверить, что найденный объём больше половины объёма исходной пирамиды. Победа!
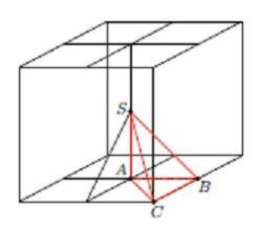
Из условия задачи вытекает, что ребро пирамиды перпендикулярно основанию
Обозначим Пирамида
является
частью изображённого на рисунке куба с ребром
причём все 48
пирамид, образующих этот куб, располагаются центрально-симметрично относительно общей вершины
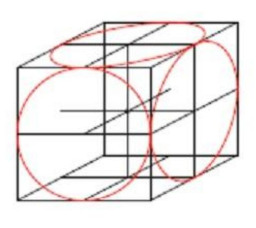
Поэтому искомый объём есть объёма тела, представляющего собой пересечение шара радиуса
и данного куба. Это
пересечение есть шар без шести шаровых сегментов с высотой шарового сегмента
(см. рисунок).
Объём этого тела:
Значит, искомый объём равен
Отметим, что объём всей пирамиды равен (или, что то же самое,
части куба, то есть
) Найденный объём
части пирамиды больше, чем
объема пирамиды, так как
Это подтверждает, что мы нашли именно объём большей части пирамиды.
Ошибка.
Попробуйте повторить позже
Основание прямой призмы – ромб
с углом
при вершине
. Точки
и
– середины ребер
и
призмы. Ребро
правильной четырехугольной пирамиды
(
– вершина) лежит на прямой
, вершины
и
- на прямых
и
соответственно. Найти отношение объемов призмы и пирамиды, если
.
Пусть — основание перпендикуляра, опущенного из точки
на ребро
. Тогда плоскость
перпендикулярна прямой
, так
как из равенства треугольников
и
следует, что и
перпендикуляр к
.
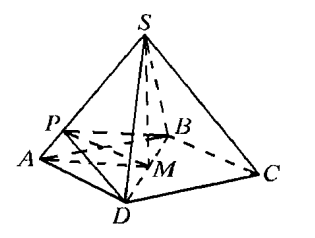
По условию прямые и
совпадают, следовательно, точки
и
лежат в плоскости, перпендикулярной прямой
. Этой
плоскостью является плоскость
, в силу того, что точка
лежит на прямой
, а прямая
перпендикулярна
пересекающимся прямым
и
этой плоскости. Таким образом, точка
является точкой пересечения прямой
и плоскости
, следовательно, точка
лежит на продолжении отрезка
за точку
и
. Далее, точка
лежит на прямой
и
, поэтому, по теореме о трех перпендикулярах,
, следовательно,
— точка пересечения диагоналей ромба
.
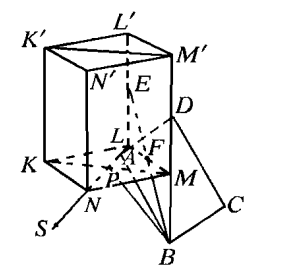
Наконец, точка равноудалена от точек
и
, поэтому
— середина ребра
, а точка
— середина отрезка
—
является центром основания
пирамиды.
Теперь искомое отношение находится несложными вычислениями. Пусть , тогда, по условию,
, поэтому
,
и объем пирамиды равен
Далее, из треугольника
находим
. Отсюда следует, что
равнобедренный треугольник, в котором
, площадь основания призмы равна
, a её высота
Таким образом, объем призмы равен
, а искомое отношение равно
.
Ошибка.
Попробуйте повторить позже
Объём правильной четырёхугольной пирамиды равен , угол между боковым ребром и плоскостью основания равен
.
Рассматриваются правильные треугольные призмы, вписанные в пирамиду так, что одно из боковых рёбер лежит на диагонали основания
пирамиды, одна из боковых граней параллельна основанию пирамиды, и вершины этой грани лежат на боковых гранях
пирамиды. Найдите объём той призмы, плоскость боковой грани которой делит высоту пирамиды в отношении
, считая от
вершины.
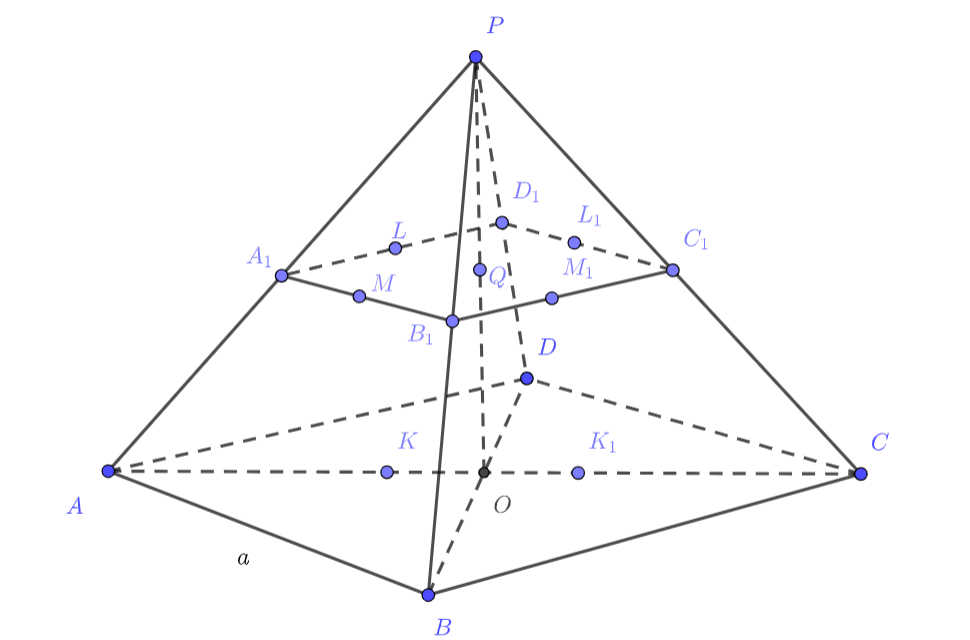
Обозначим через сторону основания
данной пирамиды
.
Пусть плоскость, параллельная основанию пирамиды и проходящая через точку лежащую на высоте пирамиды, делит высоту в
данном отношении
. Тогда в сечении пирамиды этой плоскостью получится квадрат
со стороной
(
).
Пусть боковое ребро правильной призмы
лежит на диагонали
квадрата
. Тогда вершины
противоположной грани
лежат на сторонах соответственно
квадрата
.
Из прямоугольного треугольника находим, что
Тогда если - высота равностороннего треугольника
, то
Пусть - сторона основания призмы. Тогда
. Из уравнения
находим, что
.
Обозначим . Поскольку прямоугольник
вписан в квадрат
, причём его стороны
параллельны диагоналям квадрата, то периметр прямоугольника равен сумме диагоналей квадрата, т. е.
.
Значит,
Поэтому
Выразим найденный объём через объём данной пирамиды:
Следовательно,
Ошибка.
Попробуйте повторить позже
Плоские углы трехгранного угла равны , противолежащие им ребра трехгранного угла образуют с плоскостями граней углы
,
,
. Докажите, что
Подсказка 1
Для начала давайте попробуем сделать задачу более "осязаемой". У нас есть просто множество углов и непонятно, что с ними в таком виде делать. О какой фигуре, возможно, вы подумали при виде такой конструкции? Нельзя ли в этой задаче до неё просто достроить?
Подсказка 2
Верно, мы ведь можем просто представить тетраэдр с нужным нам трехгранным углом и уже работать с ним. Давайте ещё ведём длины рёбер x, y, z тетраэдра смежных с трёхгранным углом. Выходит, нам надо доказать тройное равенство... Но просто его выводить, скорее всего, не получится. Тогда раз три произведения равны между собой, возможно, они равны чему-то общему, что от нас "спрятали". Попробуем решить задачу так. Раз мы уже зафиксировали рёбра, и углы нам даны, что не будет меняться в нашем тетраэдре?
Подсказка 3
Точно, объём у нас уже не будет меняться, а стороны мы зафиксировали сами, поэтому можно попробовать связать синусы с ними. Для нахождения объёма нужна высота и площадь основания. Не можем ли мы их просто найти из имеющихся данных?
Подсказка 4
Конечно, площадь основания находится почти "бесплатно", а высота – из конструкции с прямоугольным треугольником, у которого известна гипотенуза и угол. Осталось только выразить нужные произведения оттуда и приравнять между собой.
Рассмотрим произвольный тетраэдр, содержащий заданный трёхгранный угол. Пусть (
соответствует углу
и т.д.) — длины
смежных с трёхгранным углом сторон этого тетраэдра. Заметим, что
Где — длина высоты на грань со сторонами
, а
— её площадь,
— объём тетраэдра. Отсюда следует, что каждое
произведение равно
.
что и требовалось доказать
Ошибка.
Попробуйте повторить позже
Докажите, что если все плоские углы при некоторой вершине тетраэдра прямые, то квадрат площади грани, противолежащей этой вершине, равен сумме квадратов площадей всех остальных граней тетраэдра.
[Пространственный аналог теоремы Пифагора для прямого тетраэдра]
Подсказка 1
Попробуйте провести прямую к вершине, при которой все плоские углы прямые! Что хорошего можно сказать про получившиеся углы? А про их косинусы?
Подсказка 2
Каждый косинус можно записать как отношение проекции отрезка, лежащего на прямой к самому отрезку! Что можно сказать про сумму квадратов всех косинусов?
Подсказка 3
Да, сумма квадратов косинусов этих углов равна единице! Однако на грани мы пока так и не вышли... А если применить теорему о площади ортогональной проекции? Можно ли выразить площадь грани, противолежащей вершине (у которой все плоские углы прямые), через площади остальных граней?
Подсказка 4
Да, S1/S2 = cos(x). Отношение таких площадей равно одному из косинусов, которые получились при проведении нашей прямой! Тогда что осталось сделать, чтобы доказать требуемое?
.png)
Пусть это углы при вершине в тетраэдре
. То есть нужно доказать, что
Пусть . Отсюда
(по сути это сумма квадратов проекций
на “оси
координат” — стороны тетраэдра, делённая на само
, что равно единице из теоремы Пифагора).
По теореме о площади ортогональной проекции Выписывая аналогичные равенства для оставшихся граней,
получаем нужное соотношение
что и требовалось доказать
Ошибка.
Попробуйте повторить позже
В тетраэдре плоские углы при вершине
прямые. Пусть
— длина высоты
тетраэдра,
— длины ребер, выходящих
из вершины
. Докажите, что
Подсказка 1
Надо доказать о том, что квадрат чего-то равен сумме квадратов. Давайте для начала подумаем об аналогии с планиметрией. Нет ли там чего-то похожего и есть ли такое в стереометрии?
Подсказка 2
Верно, в планиметрии есть теорема Пифагора для прямоугольного треугольника. Но ведь и здесь у нас прямые углы, причём целых три штуки. Точно! На вебинаре МО рассказывал о таком. Осталось только выразить площади.
Подсказка 3
Ага, видим, что площадь треугольника АВС выразить сразу не получится. Но ведь нам нужно ещё воспользоваться высотой h. Может, тогда удастся вспомнить формулу, в которой она используется?
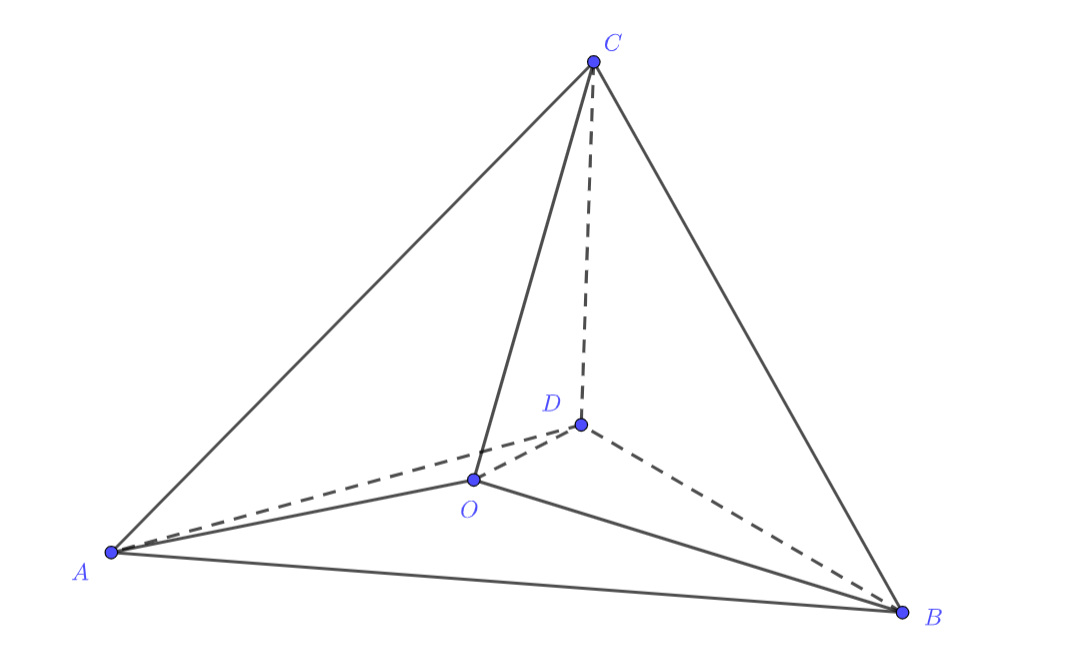
Так как все плоские углы при вершине прямые, то:
во-первых, запишем объём двумя способами:
откуда
во-вторых, по пространственной теореме Пифагора для прямоугольного тетраэдра
Выражаем площади:
Отсюда немедленно получаем:
что и требовалось доказать
Ошибка.
Попробуйте повторить позже
Докажите, что биссектор (плоскость, проходящая через ребро двугранного угла и делящая его на два равных двугранных угла) двугранного угла при ребре тетраэдра делит противоположное ребро на части, пропорциональные площадям тех граней тетраэдра, которые лежат на гранях этого двугранного угла.
Подсказка 1
Не правда ли, задача напоминает аналогичную в планиметрии с биссектрисой, только теперь вместо биссектрисы плоскость. Там мы доказывали это, выражая отношение площадей двумя способами и приравнивая их. А через что можно выразить нужные отношения в стереометрии?
Подсказка 2
Верно, можно сделать то же самое через объёмы тетраэдров, на которые разбивает биссектор исходный тетраэдр. Тогда выразим отношение объёмов через нужные площади и отрезки. Сначала давайте сделаем это для площадей, вспомнив, что мы ещё не пользовались равенством углов.
Подсказка 3
Ага, это равенство отношений мы получили. Теперь осталось получить его для отрезков. Давайте попробуем просто опустить высоты на общую грань тетраэдров. Чем тогда можно воспользоваться из планиметрии, чтобы связать высоты и отрезки грани?
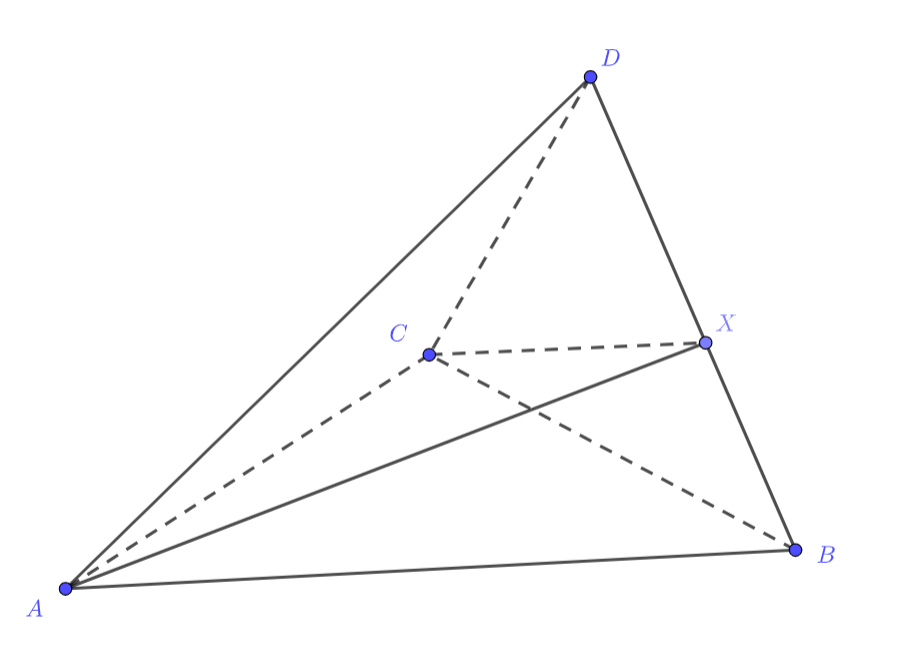
Пусть — высота треугольника
, а угол между плоскостями
и
равен
С одной стороны (расстояние от до грани по следствию из теоремы о трёх перпендикулярах падает на перпендикуляр, восставленный
из точки
в плоскости соответствующей грани):
С другой стороны (отношение расстояний до общей грани переписывается через отношение наклонных из подобия прямоугольных треугольников):
что и требовалось доказать
Ошибка.
Попробуйте повторить позже
Подсказка 1
Как нам переформулировать условие на то, что плоскость сечения параллельна BD? По какой прямой когда эта плоскость будет сечь плоскость BDS? Как при построения сечения нам поможет прямая по которой плоскость сечения пересекает BDS?
Подсказка 2
Да, эта плоскость сечет плоскость BDS по параллельной BD прямой! Значит, нам осталось найти одну точку пересечения плоскости сечения с плоскость BDS, и мы сможем построить прямую по которой плоскость сечения пересекает плоскость BDS(неопытный читатель спросит: «А зачем вообще нам искать эту прямую?». Дело в том, что если мы найдем эту прямую, то найдем по точке, которая принадлежит плоскости сечения и прямым SD и BD, а значит и плоскостям боковых граней. При этом у нас уже есть середина ребра. Так мы и построим сечение.) Осталось найти точку, как это сделать, зная, что трапеция правильная и что M лежит в плоскости сечения?
Подсказка 3
Правильно, в силу симметрии(пусть О-центр ABCD), SO и AM лежат в одной плоскости и пересекаются. И точка их пересечения, очевидно, лежит в плоскости сечения. Значит, мы нашли эту точку. Значит, и прямую, а значит построили сечение. Остается посчитать его площадь. Мы пользовались симметрией. А что еще она нам может сказать, скажем про четырехугольник, который является сечением пирамиды?
Подсказка 4
Верно, он дельтоид. Значит, его диагонали обладают некоторым свойством. Теперь посчитать площадь-дело техники, по нахождению длин диагоналей, не так ли? Конечно так, несколько подобий/теорем Фалеса и теорем Пифагора.
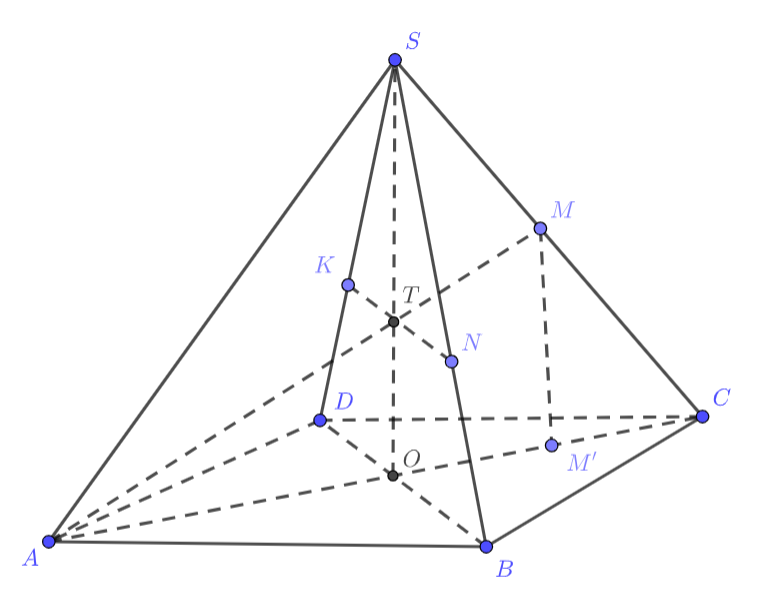
Пусть . Опустим высоту пирамиды в точку
— центр квадрата
. Далее пересечём
(все они
лежат в плоскости
), заметим, что
, откуда пересечение этой плоскостью нашей — прямая
, где
. Отсюда
будет искомым сечением. В силу
выполнено
, то есть
площадь можно найти по формуле
. Далее
— центр треугольника
, как пересечение двух медиан, то есть
. Кроме того,
. Отсюда
, а по свойству точки пересечения медиан
. В итоге
.



