Ошибка.
Попробуйте повторить позже
Степени всех вершин графа не превосходят Докажите, что его вершины можно правильным образом раскрасить в
цвет так,
чтобы одноцветные вершины не имели общих соседей.
Удалим все вершины из графа и будем возвращать их по одной, крася их, соблюдая условия раскраски. Для очередной вершины покрашено
не более её соседей и не более
её соседей через одного соседа. Следовательно, есть не более
запретов, а значит мы можем
покрасить добавленную вершину с соблюдением условий.
Ошибка.
Попробуйте повторить позже
Докажите, что вершины триангуляции выпуклого -угольника можно правильным образом покрасить в три цвета.
Ошибка.
Попробуйте повторить позже
В стране 400 городов. Некоторые из них соединены авиалиниями, а некоторые нет. Известно, что для любых 200 городов найдётся 300 пар городов, не соединённых авиалиниями. Какое наибольшее количество авиалиний может быть в стране?
Источники:
Рассмотрим граф, в котором города — вершины, а авиалинии — рёбра. Рассмотрим подграф из
вершин с наибольшим количеством
рёбер и подграф
из оставшихся
вершин.
Пусть вершина из подграфа
соединена с наименьшим количеством вершин в этом подграфе (
вершин). Предположим,
что в подграфе
имеется вершина
, которая соединена с хотя бы
вершиной из подграфа
. В таком случае
вершину
можно переместить в подграф
вместо вершины
и в нём будет больше авиалиний, что противоречит
выбору подграфа
. Следовательно, любая вершина из подграфа
связана не более чем с
вершинами из подграфа
.
Значит, между этими подграфами не более рёбер. Внутри же каждого из этих подграфов не более
рёбер.
Значит, всего в графе не более
Как известно, — это наименьшая степень вершины в подграфе
. Значит, в
не менее
рёбер. С другой
стороны, в этом подграфе не более
рёбер, откуда
. Теперь мы можем оценить количество рёбер в графе:
.
_________________________________________________________________________________________________________________________________________________________________________________
Приведём пример на рёбер. Разбиваем города на
групп по
городов. Внутри групп между городами авиалиний нет, а между
городами из разных групп — есть.
Пусть выбрано городов так, что из них
город из первой группы,
из второй,
,
— из
-й. Тогда количество пар, не
соединённых авиалиниями, будет не менее
по неравенству между средним квадратическим и средним арифметическим
Мы показали, что для произвольного подграфа в примере выполняется условие задачи.
Ошибка.
Попробуйте повторить позже
В некоторой стране некоторые пары дорог соединены односторонними дорогами; между двумя городами может быть не более одной дороги. Правительство страны хочет провести реформу, поменять направления на некоторых дорогах так, чтобы для выполнялись два свойства:
нельзя было бы выехать из города, и, проезжая по каким-то дорогам, вернуться в него же;
самый длинный простой путь по дорогам после реформы был бы не длиннее, чем самый длинный простой путь до
реформы.
Докажите, что у правительства получится это сделать. Простой путь — это такой путь, который по каждому городу проходит не более одного раза.
Рассмотрим ориентированный граф, соответствующий условию задачи. Рассмотрим среди всех ацикличных подграфов нашего графа
тот, в котором наибольшее количество рёбер. Пусть ребро не вошло в выбранный подграф. Поскольку его нельзя
добавить, то среди выбранных рёбер есть путь, идущий из
в
Хорошо известно, что в графе нет циклов тогда и
только тогда, когда его вершины можно занумеровать числами от
до количества вершин так, чтобы рёбра шли только из
вершин с меньшими номерами в вершины с большими номерами. Давайте возьмём такую нумерацию нашего подграфа, а все
рёбра, не вошедшие в подграф, обратим. Заметим, что в новом графе существует путь наибольшей длины, не проходящий
по перевёрнутым рёбрам, ведь каждое из них можно заменить на путь по неперевёрнутым: при это получится простой
путь, так как номера вершин в полученном пути возрастает. Кроме того, в нём нет циклов. Значит, полученное обращение
подходит.
Ошибка.
Попробуйте повторить позже
Ребра полного графа с вершинами покрашены в несколько цветов таким образом, что каждый цвет встречается не более
раз.
Докажите, что есть три вершины, все ребра между которыми покрашены в различные цвета.
Рассмотрим вершину из которой выходит наибольшее количество одноцветных рёбер. Пусть они
цвета. Пусть соединена первых
цветом с
Рассмотрим оставшиеся
вершину, с которыми
соединена другими цветами. Любая из этих вершин
соединена со всеми
либо первым цветом, либо тем же цветом, которым она соединена с
Однако заметим, что между
и
вершинами, отличными от
может быть не более
рёбер первого цвета, поскольку есть
рёбер
Но, как мы выяснили
ранее, имеется
вершина, не соединённая с
первым цветом. Значит, среди них есть одна вершина
такая, что
цвет всех рёбер
совпадает с цветом ребра
Но тогда из
выходит
одноцветное ребро, это противоречит выбору
Ошибка.
Попробуйте повторить позже
В стране городов, причем между любыми двумя городами проложена дорога. Министерство путей сообщения может закрыть на ремонт
любую дорогу из четырех, образующих циклический маршрут. Может ли после нескольких таких операций остаться только
дорог?
Пусть осталось дорог между
городами. Заметим, что такой граф является деревом(связность между вершинами не исчезает при
выполнении операции), а значит, двудольным. Причём обратная операция к исходной будет такая, что находится три смежных ребра и
проводится четвёртое между крайними, чтобы получался цикл из четырёх рёбер. Но в таком случае двудольность будет сохраняться,
потому что будут появляться только чётные циклы. Докажем это утверждение по индукции. Будем ввести её по количеству добавленных
рёбер при обратной операции. База, когда у нас есть просто дерево, и мы проделываем одну обратную операцию, очевидна.
Предположение, пусть на
-ой обратной операции у нас получались так же только чётные циклы. Рассмотрим граф с
-ой
операцией и уберём последнее добавленное ребро. По предположению остался граф только с чётными циклами. Попробуем
вернуть ребро. Если мы выбрали три ребра, не входящие ни в какой цикл, то получается чётный цикл. Допустим теперь
обратное. Тогда получается, что мы на самом деле заменяем три ребра в цикле чётной длины на одно ребро. Чётность
количества рёбер не меняется, а значит, и нечётных циклов появиться не могло. Таким образом, так как двудольность
сохраняется на протяжении всего процесса, то и изначальный граф должен быть двудольным, но это не так(он полный).
Противоречие.
Нет, не может
Ошибка.
Попробуйте повторить позже
Некоторые города страны соединены дорогами, причём из любого города можно доехать по дорогам до любого другого, и среди любых
городов есть какие-то два, соединённые дорогой. Докажите, что можно распределить города по не более чем
губерниям так, чтобы
города каждой губернии можно было объехать по дорогам не покидая этой губернии и не посещая ни один город более одного
раза.
Рассмотрим граф, в котором вершины — города, ребра — дороги. Нам нужно покрыть вершины этого графа непересекающимися
путями. Выберем покрытие вершин наименьшим количеством путей. Пусть в этом покрытии хотя бы
путей. Если концы каких-то двух
путей смежны, то эти два пути можно объединить в один путь, уменьшив их количество. Следовательно, если взять по одному концу от
каждого пути, образуется независимое множество из не менее чем
вершин. Но это множество противоречит условию задачи,
следовательно, путей не большее
Если два конца какого-то из путей не смежны друг с другом, то можно взять в
независимое множества оба этих конца и опять получить противоречие. Таким образом, все вершины разбиваются на
непересекающихся циклов. Вспомним, что наш граф связен, поэтому между какими-то двумя циклами должно быть ребро.
Теперь легко из этих двух циклов, соединенных ребром, сделать один путь. Таким образом, мы покрыли все вершины
путями.
Ошибка.
Попробуйте повторить позже
Чемпионат по футболу проходил в два круга. В каждом круге каждая команда сыграла с каждой один матч (за победу даётся три очка, за
ничью одно, за поражение ноль). Оказалось, что все команды вместе набрали в первом круге от общей суммы всех очков за два круга.
Известно также, что победитель чемпионата набрал во втором круге в 30 раз меньше очков, чем все команды вместе в первом круге.
Сколько команд участвовало в турнире?
Подсказка 1
Если в первом туре они набрали 60% от общей суммы очков, то выходит во втором туре они набрали 40% от общего числа очков. То есть в первом круге они набрали в 1,5 раза больше чем во втором. Как-будто это очень немало. Отсюда, хотелось бы сделать оценку на количество очков набранных за один тур.
Подсказка 2
Давайте посмотрим на один матч. За каждый матч суммарно команды получили либо 2, либо 3 очка. Но в таком случае, так как количество игр равно n(n-1)/2, где n - количество команд, то как мы можем оценить суммарное кол-во очков?
Подсказка 3
Верно, мы можем оценить, что количество очков за один тур расположено от 2*n(n-1)/2 до 3*n(n-1)/2. Значит, если количество очков в двух турах отличается в 1,5 раза, то так как во втором туре хотя бы 2*n(n-1)/2, а в первом не более 3*n(n-1)/2, то их отношение хотя бы 3/2. При этом, понятно, что тогда в первом туре ровно 3n(n-1)/2 очков, а во втором ровно 2n(n-1)/2. Но тогда, в первом туре ничьей не было, а во втором все сыграли в ничью. Осталось только применить это знание и факт того, что победитель во втором туре набрал в 30 раз меньше очков чем все суммарно в первом и получить ответ.
Пусть в турнире участвовало команд. Заметим, что в каждом матче две команды в сумме получают 2 или 3 очка. Значит,
общее количество очков, которые могут набрать все команды в одном круге, не меньше, чем
, и не больше, чем
. Из условия следует, что все команды вместе набрали в первом круге ровно в полтора раза больше очков, чем во
втором (
всех очков в первом круге и
во втором). Но это возможно лишь в случае, если в первом круге все
матчи закончились победой одной из команд (общая сумма очков
), а во втором - ничьей (общая сумма очков
). Значит, победитель набрал во втором круге
очков. По условию,
, откуда находим
.
Ошибка.
Попробуйте повторить позже
Дан граф на
вершинах: сопоставим каждой вершине
переменную
. Пусть
— множество остовных
деревьев графа
(то есть поддеревьев, содержащих все вершины). Рассмотрим остовный многочлен от
переменных
Назовем связный граф хорошим, если раскладывается на линейные множители (в частности, если
— тождественный
ноль), иначе плохим.
1. Найдите , где
— полный граф на 4 вершинах.
2. Докажите, что цикл на пяти вершинах является плохим графом.
3. Пусть — хороший граф,
— некоторое подмножество его вершин. Граф
состоит из всех вершин, лежащих в
, и всех ребер
графа
, соединяющих эти вершины. Докажите, что граф
тоже хороший.
4. Назовём раздвоением вершины операцию, добавляющую в граф вершину
, соединенную ровно с теми же вершинами, что и
.
Докажите, что граф, получающийся из одной вершины операциями добавления висячей вершины, раздвоения вершины с добавлением ребра
и раздвоения вершины без добавления ребра
, является хорошим.
Источники:
1. В полном графе на четырех вершинах есть только 2 вида остовных деревьев: 1) цепь длины 4; 2) три вершины, "висящие"на четвертой.
Каждое дерево первого вида даст в остовный многочлен одночлен ,
, причем каждый одночлен будет представлен 2
раза.
Каждое дерево второго вида даст в остовный многочлен одночлен , где
— "вершина"остова.
В итоге получим многочлен:
2. Распишем . Поскольку многочлен
линеен по каждой переменной, получаем,
что каждая из переменных живет только в одной из скобок. Тогда переменные вынуждены разбиться на скобки 2-2-1 или 3-1-1, что дает нам
не более четырех мономчиков, противоречие.
3. Давайте сначала заметим, что можно последовательно выкидывать вершины по одной с сохранением связности, если связно. (Если
несвязно, то просто 0 получится и все).
Для этого нужно подвесить за и поочередно удалять вершины с самого нижнего уровня. Теперь нужно понять, что при удалении
только одной вершины
граф остается хорошим. Для этого подставим 0 в
. Получим, что все слагаемые, в которые
входило в хотя
бы первой степени, обнулились, а значит остались в точности те, где
— висячая вершина. А все такие деревья устроены так: выбрано
дерево в графе
, и потом одна из вершин из окрестности
соединена с
. Тогда многочлен после подстановки нуля равен
. Подстановка нуля сохраняет раскладываемость на множители, значит
тоже раскладываемый,
значит, при удалении вершины
граф останется хорошим.
4. Сначала докажем вспомогательный факт про такой тип графов.
Лемма о раздвоении без добавления ребра. Пусть дан граф на
вершинах. Рассмотрим граф
, полученный из
добавлением вершины
и соединением ее со всеми вершинами из
, но не самой
. Тогда
Доказательство. Давайте заметим, что любое дерево в графе устройство следующим образом — на всех вершинах, кроме
,
берется некоторый лес, такой, что в каждой компоненте есть хотя бы одна вершина из
, и потом вершина
соединяется с ровно
одной вершиной из каждой компоненты. Обозначим за
множество всех таких лесов, за
— число компонент связности в лесу
, и назовем
пересечения множеств
с компонентами связности леса
. Тогда из рассуждений
выше
Теперь давайте поймём, как устроены деревья в . Там мы тоже берём лес, который содержит все вершины, кроме
,
, и
такой, что каждая его компонента содержит хотя бы одну вершину из
, после чего одна из долей соединяется с обеими вершинами
из
и
, а каждая из остальных
долей — с ровно одной из этих вершин. Тогда в тех же обозначениях получается,
что
Теперь очевидно, что второй сомножитель равен , и лемма доказана.
________________________
Пусть - граф из леммы 1. Мы в лемме 1 уже выяснили как устроены деревья в графе
, поэтому нужно разобраться с тем, как они
устроены в
. Заметим, что они устроены так: мы снова берем лес с такими же условиями, а дальше делаем одно из двух -
либо не проводим ребро между
и
, и это слагаемое такое же как в
, либо проводим, и тогда каждую из
долей соединяем с ровно одной из этих вершин. Стало быть, сумма всех первых слагаемых даст нам
, а сумма вторых
равна
Тогда получается, что
доказали требуемое.
Ошибка.
Попробуйте повторить позже
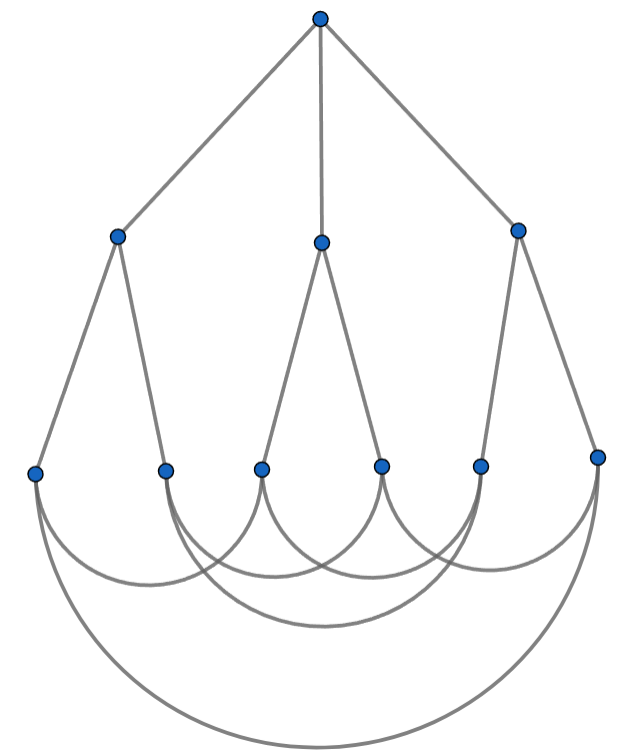
В графе степени всех вершин равны и между любыми двумя вершинами существует путь длиной не более
Какое наибольшее число
вершин может быть в этом графе?
Рассмотрим вершину Она соединена с тремя вершинами
и
Получается, что все остальные вершины должны быть
соединены с какой-то из вершин
иначе между ними и
не будет пути длиной не более
Вершины
могут быть соединены
суммарно не более чем с
вершинами помимо
Значит, всего не более
вершин. Пример на
вершин представлен
ниже:
Ошибка.
Попробуйте повторить позже
В некой стране городов (города считайте точками на плоскости). В справочнике для каждой пары городов имеется
запись, каково расстояние между ними (всего
записей). Пусть стерлись
записей, и известно, что в этой стране
никакие три города не лежат на одной прямой. При каком наибольшем
всегда можно однозначно восстановить стершиеся
записи?
Первое решение. Индукцией покажем, что для городов
База очевидна.
Шаг индукции. Пусть для городов стёрто не более
записей. Выберем город
для которого стёрто хотя бы одно расстояние
до другого города, и рассмотрим остальные
городов. Между ними стёрто не более
расстояний, и по предположению индукции
можно восстановить все эти расстояния, а тогда и взаимное расположение этих городов на плоскости. Для города
известны расстояния по крайней мере до трёх городов, и это позволяет однозначно восстановить его расположение. Увеличить
до
нельзя. Пусть неизвестны расстояния от точки
до всех точек, кроме
и
Тогда положение точки
определено с точностью до симметрии относительно прямой
значит, расстояния от неё до остальных точек не
восстанавливаются.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Рассмотрим граф со вершинами и
рёбрами, соответствующими стёртым записям. Этот граф содержит не
менее четырёх компонент связности. Зафиксируем по вершине
) в каждой из этих четырёх компонент. Все расстояния между
этими вершинами известны. Рассмотрим произвольную вершину первой компоненты. Известны её расстояния до точек
следовательно, положение соответствующего города на плоскости определено однозначно. Аналогична ситуация с вершинами оставшихся
компонент.
Ошибка.
Попробуйте повторить позже
Промежуток из одного или несколько подряд идущих дней назовём нечётным, если нечётное число из этих дней были дождливыми. Каково наибольшее возможное число нечётных промежутков в июле?
Назовём префиксом какое-то количество первых дней июля. Всего префиксов (может быть префикс из
дней). Тогда любой
промежуток является разностью двух префиксов. Нетрудно понять, что промежуток будет нечётным, если он является разностью
префиксов разной чётности.
Рассмотрим граф, в котором вершинами являются префиксы. Ребром соединим префиксы, у которых разная чётность.
Получился двудольный граф, в котором вершин соответствуют чётным префиксам и
— нечётным. В двудольном
графе не более
рёбер. То есть всего не более
промежутков. В качестве примера можно сделать все дни
дождливыми.
Ошибка.
Попробуйте повторить позже
Грани куба разбиты на клетки со стороной
Каждую клетку покрасили в красный, жёлтый или зелёный цвет так,
что клетки, имеющие общую сторону, покрашены в разные цвета. Какое наименьшее количество красных клеток могло
быть?
Оценка. Три квадрата при вершине куба образуют цикл соседних квадратов длины Вокруг него образуется ещё один цикл длины
из
соседних клеток. А вокруг него — цикл длины
Взяв вокруг двух противоположных вершин куба по три таких цикла, а вокруг
остальных вершин — по два малых цикла, получим
непересекающихся нечётных циклов. Поскольку нечётный цикл в два цвета
правильно покрасить нельзя, каждый из них содержит чёрную клетку.
Пример. Красим боковые грани куба в шахматном порядке в жёлтый и зелёный. В основаниях красим главные диагонали красным,
остальное докрашиваем в шахматном порядке жёлтым и зелёным.
Ошибка.
Попробуйте повторить позже
На чемпионат по игре в шляпу приехало команд, в каждой из которых по два человека. Все
участников произвольным образом
уселись за круглый стол. После этого все спохватились, что игру можно начать, только когда люди из одной команды будут сидеть
напротив. За одно действие разрешается поменять любых двух участников местами. Какое наименьшее число действий придется совершить,
чтобы гарантировано можно было начать игру?
Построим граф, в котором вершинами обозначим места за столом. Две вершины будем соединять ребром, если соответствующие места
находятся напротив друг друга, или если на соответствующих местах сидят напарники по команде. В построенном графе степень каждой
вершины равна (если сокомандники уже сидят напротив друг друга, то они соединены двумя рёбрами). По лемме о хороводах этот граф
представляет из себя один или несколько непересекающихся циклов. Заметим, что если мы поменяем местами двух напарников, граф не
изменится. Допустим, мы меняем местами двух находящихся в одном цикле людей
и
из разных команд. Обозначим их напарников
через
и
Сперва допустим, что
и
находятся на одной и той же из двух дуг, на которые
и
разбивают цикл. В этом случае
наш цикл остается циклом:
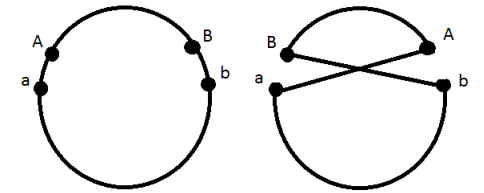
Допустим теперь, что и
находятся на разных дугах. В этом случае наш цикл распадается на два:
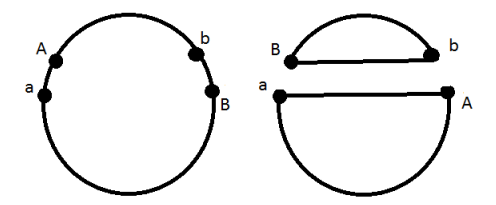
Теперь рассмотрим случай, когда мы меняем местами людей из разных циклов. В этом случае оба цикла "склеиваются"в один:
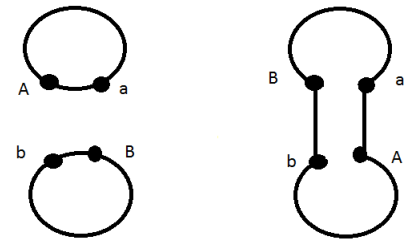
В каждом из случаев число циклов в графе за одну операцию можно увеличить не более чем на один. Если изначально каждый
из участников сидит рядом со своим напарником, то граф представляет из себя один цикл. Мы должны получить граф,
состоящий из циклов длины
Так как на каждом шаге число циклов возрастает не более, чем на
добиться этого
менее чем за
шагов нельзя. Отметим, что любой цикл длины более чем
можно за одну операцию разбить на два
меньших, т.е. за
операций можно от любого начального расположения прийти к ситуации с
циклами, т.е. к искомой
ситуации.
Ошибка.
Попробуйте повторить позже
На свободные поля шахматной доски по одному выставляются короли. Первый выставляется произвольно, каждый следующий должен бить нечетное число ранее выставленных. Какое наибольшее число королей можно выставить?
Для начала покажем, что поставить не получится. Предположим, что мы смогли это сделать. Рассмотрим граф, в котором короли — это
вершины. Рёбрами соединим королей, которые друг друга бьют. Тогда, с одной стороны, мы получили граф, в котором
рёбер (потому что все короли бьют всех королей на всех соседних клетках). С другой же стороны, каждый раз добавляя
очередного короля (кроме первого), мы добавляли в граф нечётное количество рёбер. В граф нечётное количество раз
(
) было добавлено нечётное количество рёбер. Значит, количество рёбер в графе должно быть нечётным. Пришли к
противоречию.
Теперь приведём пример на Нужно ставить королей в следующем порядке на клетки с координатами:
Ошибка.
Попробуйте повторить позже
Определение. Назовем полный ориентированный граф почти транзитивным, если можно сменить направление ровно одного ребра так, чтобы в полученном графе не было ориентированных циклов.
Докажите, что любой полный сильно связный ориентированный граф не являющийся почти транзитивным. Докажите, что
существуют два сильно связных подграфа
и
графа
(не совпадающие с
), имеющих ровно
общую вершину, содержащие в
объединении все вершины графа
Лемма. В сильно связном турнире существует гамильтонов цикл.
Доказательство. В сильно связном турнире есть циклы. Рассмотрим в нашем турнире максимальный простой цикл
Предположим, что в него вошли не все вершины графа, пусть вершина
не вошла в этот цикл. Пусть не все стрелки между
и циклом
ориентированы одинаково. Тогда существуют последовательные вершины цикла
и
такие, что
В этом случае несложно удлинить максимальный цикл
вставив вершину
между
и
противоречие.
Пусть из всех вершин цикла стрелки входят в
Ввиду сильной связности турнира
существует путь
от
до цикла
Пусть
впервые пересекает цикл
в вершине
Тогда, опять же, несложно удлинить наш максимальный цикл,
заменив стрелку
на путь
Противоречие. Случай, когда из
выходят ребра ко всем вершинам цикла
аналогичен.
_________________________________________________________________________________________
Вернемся к доказательству основной задачи. По лемме в есть гамильтонов цикл
. Нумерация вершин — циклическая,
то есть
Пусть длина диагонали
цикла
— это остаток от деления на
числа
Если количество вершин в равно
или
то
почти транзитивен.
Далее Рассмотрим два случая. Будем говорить, что
если в
ребро между
и
направлено к
1. Для каждого выполняется
Тогда пусть состоит из всех вершин с нечётными номерами,
— из
и всех вершин с чётными номерами. Нетрудно видеть, что
а индуцированные турниры
и
— сильно связные.
2. Существует диагональ
Не умаляя общности будем считать, что Докажем, что при
диагональ
Пусть это не так, тогда
выберем диагональ
где
и
— максимально. Понятно, что выполняется хотя бы одно из
условий
и
Пусть
(второй случай аналогичен). Тогда
следовательно, для множеств
и
индуцированные турниры
и
сильно связны,
В этом
случае утверждение доказано.
Итак, при и
мы имеем
Осталось разобраться, как направлены стрелки, инцидентные
Если
существует такое
что
то множества
таковы, что турниры и
сильно связны и
В этом случае утверждение доказано.
Остаётся случай, когда для некоторого в нашем графе стрелки ориентированы таким образом:
При турнир
почти транзитивен (с порядком
). При
турнир
почти транзитивен (с порядком
). Если же
то
Следовательно, множества
и
таковы, что
и
сильно связны и
Ошибка.
Попробуйте повторить позже
В каждый город ведет дороги: красная, синяя и белая. В зависимости от цветов входящих дорог, считая по часовой
стрелке, города разделяются на два типа: КСБ и КБС. Докажите, что разность количеств городов разных типов делится на
Заменим каждую белую улицу города на две, синюю и красную, соединив синим цветом концы синих улиц, соседних с белой, а красным
цветом — концы соседних с ней красных улиц (см. рис. ). В соответствии с рисунками рис.
будем называть белые улицы
улицами типов
и
а их количества обозначим соответственно
и
В случаях, изображенных на рис.
и рис.
будем
считать, что красная и синяя улицы, которыми мы заменили белую, пересекаются в точке, отличной от вершин ломаных, которыми
являются эти улицы.
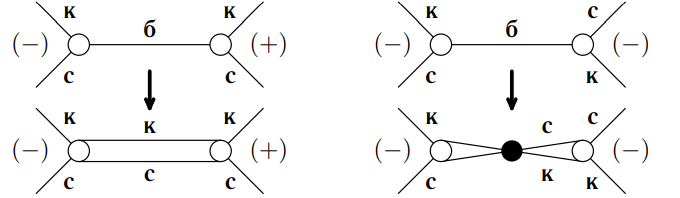
Рисунки и
и соответственно.
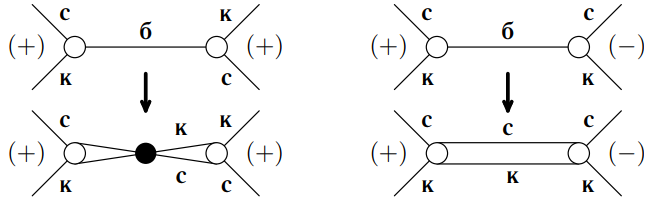
Рисунки и
и соответственно.
Теперь все синие улицы образуют несколько многоугольников. Назовем их синими. Аналогично, красные улицы образуют несколько
красных многоугольников. Ясно, что границы двух многоугольников разного цвета либо не пересекаются, либо пересекаются в четном числе
точек (если границы пересекаются, то граница одного из многоугольников входит внутрь второго столько же раз, сколько и выходит из
него). Но число точек пересечения границ многоугольников разного цвета равно числу белых улиц типов и
т. е.
Значит,
число
— четное.
Остается заметить, что разность между числом положительных и числом отрицательных перекрестков равна и,
следовательно, кратна четырем.
Ошибка.
Попробуйте повторить позже
В некоторой стране каждый город соединен с каждым дорогой с односторонним движением. Докажите, что найдется город, из которого можно добраться в любой другой не более чем с одной пересадкой.
Докажем утверждение задачи по индукции. Для двух городов утверждение очевидно. Пусть верно для городов, докажем для
Выкинем некоторую вершину
и все рёбра, с концом в этой вершине. Для оставшегося графа верно предположение индукции, то есть
существует вершина
такая, что из него можно добраться до любой другой по не более, чем
рёбрам. Пусть из вершины
напрямую
можно добраться в вершины
а только через другую вершину в
Если из вершины
или из какой-нибудь из
вершин
ребро ведёт в
то вершина
по-прежнему подходит. Если же во все эти вершины ведут рёбра из
то
подойдёт вершина
в вершины
можно попасть непосредственно, а в вершины
— через вершины
Ошибка.
Попробуйте повторить позже
Про натуральные числа и
известно, что они различны и не превосходят 100. Мы можем выписать любую последовательность
, содержащую все натуральные числа от 1 до 100. Какое наименьшее число последовательностей нужно
выписать, чтобы среди них наверняка имелась такая, в которой два или три подряд идущих члена принадлежат множеству
Источники:
Подсказка 1
Для начала нужно понять, как вообще подступаться к такой задаче. Через что её решать? У нас есть числа, и мы рассматриваем, стоят ли они подряд в последовательностях. Какая вещь помогает рассмотреть отношения между какими-то объектами?
Подсказка 2
Это графы! Пусть у нас есть какое-то количество последовательностей. Вершины графа - это числа от 1 до 100, а рёбра между вершинами x и у проводятся, если в одной из последовательностей числа х и у были подряд идущими членами. Теперь надо понять, при каком наименьшем числе последовательностей обязательно не найдется тройки, внутри которой нет рёбер.
Подсказка 3
Если сложно угадать число, попробуйте рассмотреть ситуацию, когда у нас n последовательностей. Как тогда можно оценить степени вершин?
Подсказка 4
В каждой последовательности число соседствует не более чем с двумя другими числами, то есть степень каждой вершины не превосходит 2n. Подумайте, при каком наименьшем n в любой тройке вершин будет хотя бы одно ребро. Это и будет ответом на задачу. И не забудьте про пример!
Сначала покажем, что последовательностей не хватит.
Построим граф, вершины которого это числа от до
, а рёбра между вершинами
и
проводятся, если в одной из
последовательностей числа
и
были подряд идущими членами.
Так как суммарно во всех -x последовательностях каждое число будет соседом не более
других чисел, степень каждой
вершины в этом графе не превосходит
.
Тогда выберем в графе две несмежные вершины Так как степень каждой из них не более
, а всего вершин
, то найдется
хотя бы
вершина
, которая не соседствует с обеими вершинами
. Тогда множество чисел
не будет
удовлетворять условию задачи (ни в одна последовательности нет двух или трех подряд идущих членов, которые содержатся в
)
_________________________________________________________________________________________________________________________________________________________________________________
Пример на последовательностей опишем пример в терминах графа.
Разделим чисел на две равные группы: например,
и
.
Отдельно расставим первые чисел в
последовательностей длиной
, чтобы любые
числа были соседями в хотя бы одной из
последовательностей. (То есть на языке графов: нужно покрыть
путями полный граф на
вершинах). И аналогично поступим
со второй группой
чисел, а потом просто “склеим” последовательности. Например, если первая последовательность
в первой группе это
, а первая последовательность во второй - это
, то склеиваем и получаем
.
Опишем построение последовательностей длиной
. Поместим вершины в правильный многоугольник и покроем полный граф на
этом подмножестве вершин
последовательностями (то есть путями проходящими по всем вершинам), идущими зигзагом через
многоугольник с поворотом каждого пути на кратный
угол. На картинке пример построения
последовательностей, для
чисел:
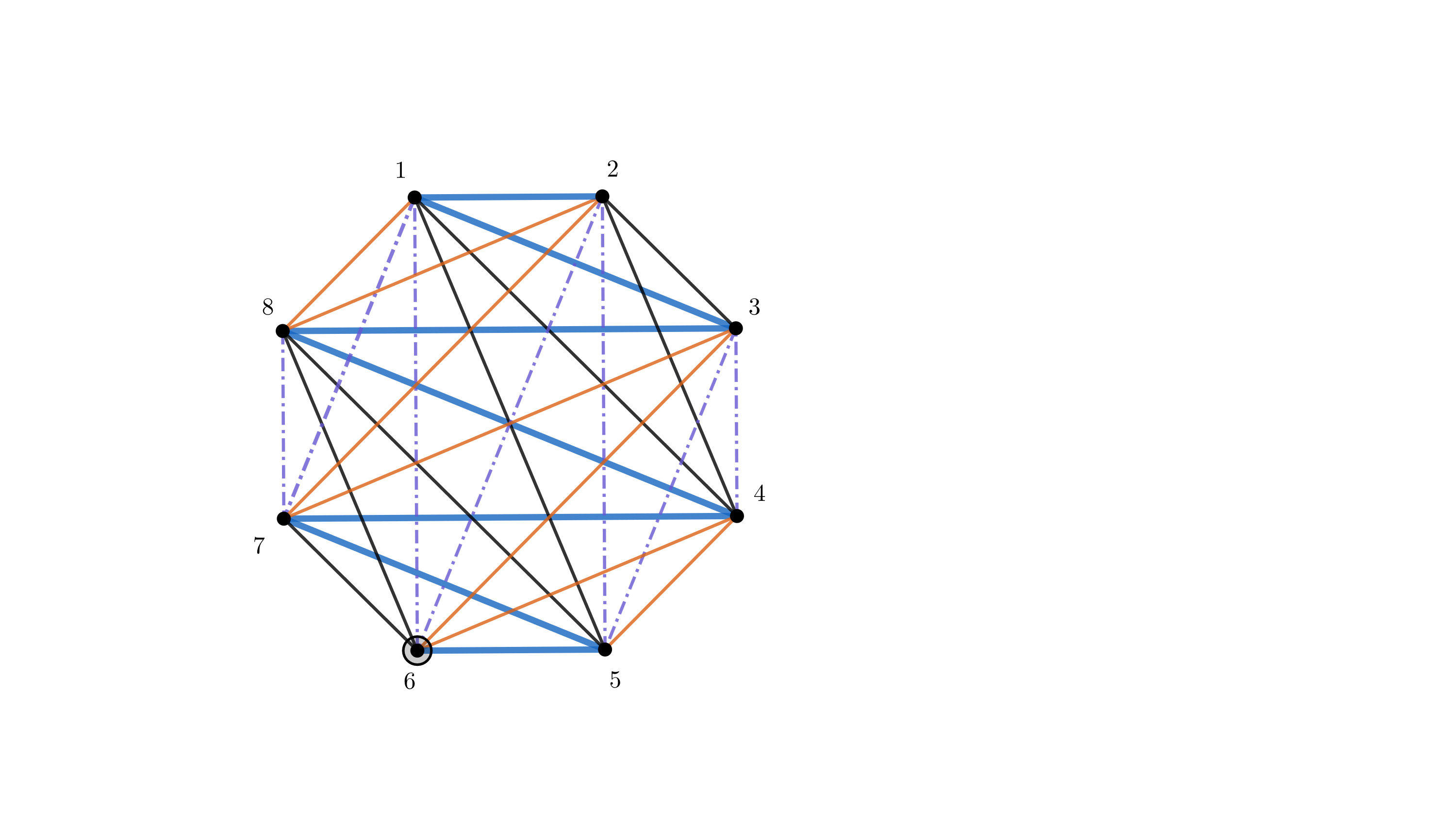
Теперь поясним, почему после "склейки"полученные последовательностей будут удовлетворять условию. Какие бы
числа
, мы ни взяли, либо два из них будут среди чисел от
до
, либо среди чисел от
до
. Тогда два
числа из одно группы соединены ребром, то есть являются соседями в одной из
последовательностей. Этого мы и
добивались.
Ошибка.
Попробуйте повторить позже
Деревни некоторой языческой страны соединены дорогами так, что от любой деревни можно добраться до любой другой не проходя ни через какую деревню дважды, причём сделать это можно единственным способом. В каждой деревне живет свое племя туземцев. Каждое племя поклоняется одному из трёх идолов: Камню, Ножницам или Бумаге. Известно, что Камень сильнее Ножниц, Ножницы сильнее Бумаги, а Бумага сильнее Камня. Каждое племя желает, чтобы их идол был не слабее, чем идол любого из соседствующих с ними племен. С этой целью каждый вечер ровно в 20:24 каждое племя смотрит на своих соседей и, если обнаруживает соседа с более сильным идолом, меняет свои верования, начиная поклоняться этому более сильному идолу. Верно ли, что рано или поздно все племена начнут верить в одного и того же идола?
Источники:
Подсказка 1
Если видите в задаче ребят и дружеские связи, города, дороги и тому подобное, то сразу же переводите задачу на язык графов, так с ней намного удобнее будет работать. Обозначим города за вершины, а дороги между ними за ребра. Поверим в лучшее и попробуем доказать, что всё-таки все вершины будут иметь одного идола в конце. Подумайте над тем, какой перед нами граф и как он поможет нам в доказательстве.
Подсказка 2
В условии сказано, что существует единственный простой путь (без повторения вершин) между любыми двумя вершинами, значит, перед нами граф-дерево, а у такого графа есть «листья» (вершина, у которой есть только один «сосед»). Попробуйте доказать необходимое утверждение по индукции, рассмотрев граф на n вершин, для которого оно выполняется, а шагом индукции пусть будет добавление «листа».
Подсказка 3
Возьмем две вершины нашего графа, вершину A – лист, вершину B – родитель вершины A (единственный её «сосед»). Рассмотрите два случая, когда вершина B не меняла своего идола на идола вершины A и когда меняла. Если в каждом из случаев в графе идолы всех вершины становятся одинаковыми, то мы доказали утверждение.
Подсказка 4
Пусть B не меняла своего идола на идола вершины A, значит, либо идол B сильнее идола вершины A, либо их идолы равны. В каждом из этих случаев в один момент идолы вершин A и B будут равны, а по предположению индукции и весь граф будет иметь одинаковых идолов. Осталось аналогичным способом рассмотреть случай, когда B поменяла своего идола на идола вершины A.
Переформулируем условие задачи на язык графов. Каждому племени поставим в соответствие вершину, между любыми двумя соседними проведем ребро. Для каждой вершины определен ее идол, если идол соседней вершины сильнее, то в этот день вершина меняет своего идола на более сильного.
Будем решать задачу индукцией по количеству вершин. База индукции для графа, состоящего из одной вершины, очевидна.
Докажем, что если условие задачи верно для некоторого натурального , то оно же верно для
. Выберем висячую вершину
исходного дерева, родителем которой является вершина
.
Будем говорить, что вершина влияет на вершину
, если данные вершины являются соседями и идол
сильнее идола
, при
этом
не имеет соседа с более сильным идолом, отличным от
.
Если не существует дня, в котором вершина влияло на вершину
. В графе, полученном из данного удалением вершины A, по
предположению индукции все вершины через несколько дней будут иметь одного и того же идола, в частности его же будет иметь вершина
, а значит и вершина
.
Предположим, что существует день, в котором повлияло на
. После этого дня вершины
и
имеют одинакового идола.
Теперь, если вершина B меняет идола на более сильного, то на следующий день
так же начинает поклоняться этому идолу, а значит
не наступит дня, в котором
имело бы более сильного идола, следовательно
больше никогда не повлияет на
,
тем самым мы можем применить рассуждения, проделанные ранее, для дня, после которого вершина
повлияла на
.



