Задачи с параметром —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Задачи с параметром

Тема АЛГЕБРА

Задачи с параметром

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Разделы подтемы Задачи с параметром

Алгебра (+ логика). Связь между множествами решений

Алгебра. Теорема Виета

Алгебра. "Гвозди" для квадратичной функции

Алгебра. Исследование замены

Алгебра (+ логика). Несколько неизвестных или несколько параметров

Алгебра. Задачи без идеи, решающиеся аналитически

Алгебра в xOa (решение относительно параметра)

Графика. Прямые, пучки прямых, движение

Графика. Гипербола

Графика. Окружности: касание, пересечение, связь с другими объектами

Графика. Функции с модулем: галочка, корыто и другие

Графика. Отрезок, ромб, квадрат

Графика. Множество касательных, арктрига и прочее

Графика в xOa (параметр как вторая неизвестная)

Симметрия (и чётность) в параметрах

Монотонность и производная в параметрах, уравнения вида f(t) = f(z) или f(f(x)) = x

Метод главного модуля/слагаемого в параметрах

Непрерывность в параметрах

Исследование области значений функции (в том числе a = f(x))

Метод оценки (метод мажорант) в параметрах

Подтемы раздела алгебра

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#88268

При каких значениях параметра $a$ решением неравенства

2 2 2 x − (a − 2a− 3)x+ a +2 ≤0

является отрезок $[2;3]?$

Подсказки к задаче

Подсказка 1

Перед нами парабола — что можно сказать про её график? Куда направлены ветви такой параболы?

Подсказка 2

Нужно разобраться с условием на f(2) и f(3): какими должны быть эти значения, чтобы решением был именно отрезок [2; 3]? Ещё, конечно, можно поставить условие на дискриминант, но может оно нам и не необходимо?

Показать ответ и решение

Рассмотрим множество функций

2 2 2 fa(x) =x − (a − 2a− 3)x +a + 2

При каждом фиксированном $a$ это квадратичная функция, графиком которой является парабола с ветвями, направленными вверх. При этом она может выглядеть как (1) $(D = 0),$ (2) $(D > 0)$ или (3) $(D< 0):$

$PIC$

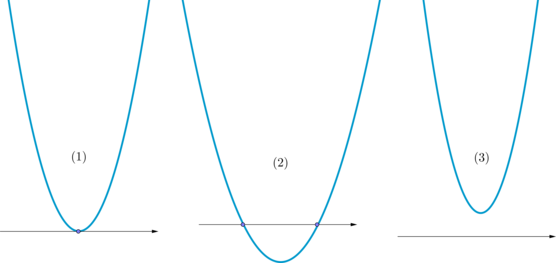
Для того, чтобы решением неравенства являлся отрезок $[2;3],$ необходимо, чтобы парабола выглядела как (2), то есть необходимо выполнение следующих условий:

(| 2 2 2 ||{ D =(a − 2a − 3) − 4(a + 2)> 0 || fa(2)= 0 |( fa(3)= 0 ( |||{ (a2− 2a− 3)2− 4(a2+ 2)> 0 a2− 4a − 12= 0 |||( a2− 3a − 10= 0 ( { (a2− 2a− 3)2− 4(a2+ 2)> 0 ( a= −2

Заметим, что при $a= −2$ неравенство $(a2− 2a − 3)2− 4(a2+2)> 0$ выполняется, так как оно равносильно $1> 0.$ Следовательно, получаем

a ∈{−2}

Замечание.

Первое условие системы можно считать избыточным в том смысле, что дискриминант автоматически положителен при условии $f (2)= f (3)= 0, a a$ поскольку квадратный трехчлен имеет два корня $x = 2$ и $x =3.$

Ответ:

$a ∈{−2}$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#88267

При каких значениях параметра $a$ число 3 заключено между корнями уравнения

2 x − (2a − 1)x+ 4− a =0 ?

Подсказки к задаче

Подсказка

У вас есть парабола. Куда направлены её ветви? Для наглядности, можете нарисовать рисунок и посмотреть: какое ограничение на f(3) надо наложить, чтобы точка x = 3 заключалась между корнями?

Показать ответ и решение

Рассмотрим функцию

2 y = x − (2a− 1)x +4− a

Ее графиком является парабола, ветви которой направлены вверх и которая должна пересекать ось абсцисс в двух точках. Чтобы выполнялось условие задачи, нужно, чтобы парабола выглядела так:

$PIC$

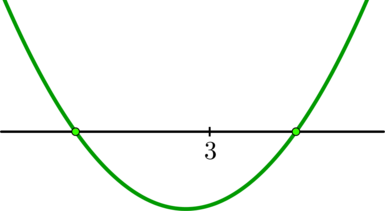
Значит, необходимо:

16 y(3)< 0 ⇒ a> 7-

Ответ:

$a ∈( 16;+∞ ) 7$

Ошибка.
Попробуйте повторить позже

Задача 3#88176

При каких $a$ неравенство

2 ax + (a+1)x− 3< 0

выполняется при всех $x < 2$ ?

Показать ответ и решение

$1)$ Если $a =0,$ то неравенство становится линейным:

x− 3< 0

Это неравенство выполнено при всех $x< 2,$ поэтому $a= 0$ нам подходит.

$2)$ Если $a> 0,$ то парабола $y = ax2+(a+ 1)x − 3$ будет иметь ветви, направленные вверх. Тогда неравенство выполняется не для всех $x <2$ (при $x→ −∞ y(x)→ +∞$ )

$3)$ Если $a< 0,$ то парабола $y = ax2+ (a +1)x− 3$ будет иметь ветви, направленные вниз. Рассмотрим дискриминант этого квадратичного трехчлена

2 2 D= (a+ 1) − 4⋅(− 3)⋅a =a + 14a+1

1.

Если $D < 0,$ то парабола находится ниже оси абсцисс. Тогда неравенство $ax2+ (a+ 1)x− 3< 0$ выполнено при любых $x,$ в частности, при всех $x< 2.$

$PIC$

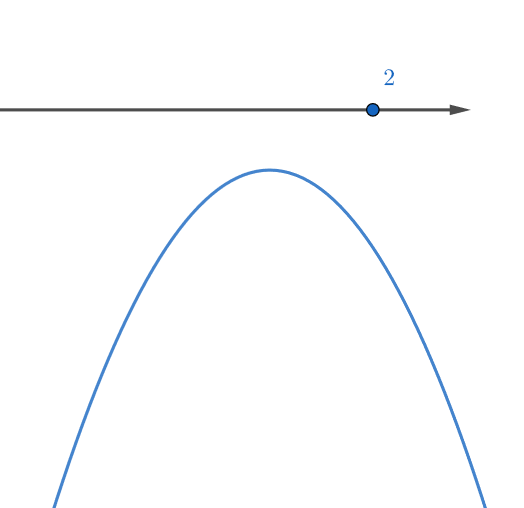
Решая квадратное неравенство $a2+ 14a+ 1< 0$ получаем $a∈ (− 7− 4√3;−7 +4√3).$

2.

Если $D = 0,$ то неравенство будет выполнено при всех $x <2$ , если вершина параболы $y =ax2+ (a+1)x− 3$ будет удовлетворять условию $x(верш) ≥2.$

$PIC$

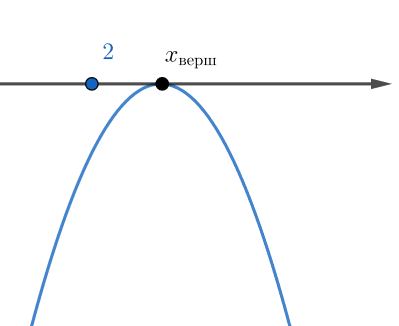
То есть

− a+2a1≥ 2

Условие на вершину будет выполнено только для корня дискриминанта, равного $− 7+4√3.$

3.

Если $D > 0,$ то неравенство будет выполнено при всех $x <2$ , если вершина параболы $y =ax2+ (a+1)x− 3$ будет удовлетворять условию $x ≥2, (верш)$ а также $y(2)< 0.$

$PIC$

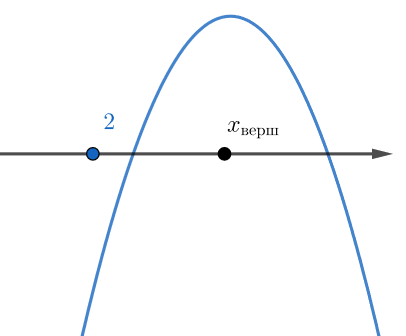
Эти условия задаются системой:

( ||||{ a< 0 D > 0 ||||( x(верш) ≥2 y(2)< 0

Решая систему, получим $√- a∈ (−7+ 4 3;0)$

В итоге, получаем ответ:

√- a ∈(−7− 4 3;0]

Ответ:

$a ∈(−7− 4√3;0]$

Ошибка.
Попробуйте повторить позже

Задача 4#88175

При каких $a$ оба корня уравнения

2 2 x − 6ax+ 2− 2a+ 9a = 0

больше трех?

Подсказки к задаче

Подсказка 1

Нарисуем график! Мы знаем, что это парабола ветвями вверх. Какие необходимые и достаточные условия нужно наложить на график, чтобы оба корня нашего уравнения были больше 3?

Подсказка 2

Абсцисса вершины параболы должна быть правее 3; дискриминант больше нуля; значение в точке 3 положительно

Подсказка 3

У нас получилась система из трёх уравнений относительно а, осталось лишь решить её и получить область возможных значений параметра!

Показать ответ и решение

Рассмотрим параболу $y = x2− 6ax +2− 2a+ 9a2.$ Её ветви направлены вверх. Зададим при помощи графика условия, эквивалентные тому, что оба корня больше $3.$

$PIC$

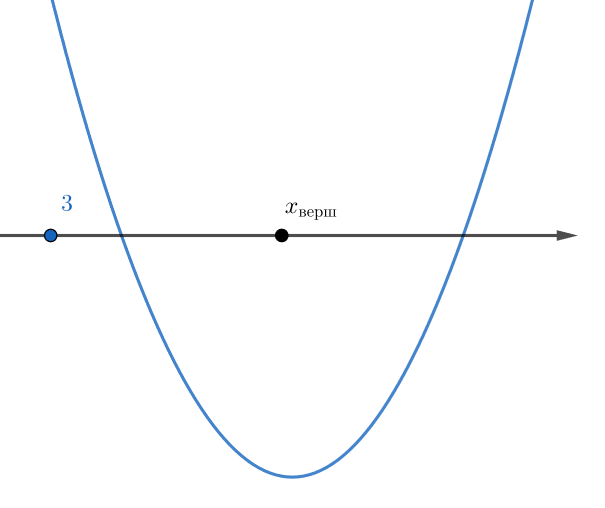
Получим систему:

( |{ D >0 | x(верш) >3 ( y(3)> 0

Подставим выражения для дискриминанта, абсциссы вершины и значения в точке $x= 3:$

( |{ 36a2 − 4(2− 2a+ 9a2)>0 |( 3a> 3 9− 6a⋅3+2 − 2a+ 9a2 >0

( |{ 8a− 8> 0 |( a >1 9a2− 20a +11> 0

Решение системы:

a> 11 9

Ответ:

$(11;+∞) 9$

Ошибка.
Попробуйте повторить позже

Задача 5#88067

Придумайте какую-нибудь систему из двух уравнений с двумя неизвестными $x$ и $y$ , решениями которой были бы все такие пары целых чисел $(x,y)$ , которые удовлетворяют системе неравенств

{ y ≤ 1000 − x2 2 y ≥ x

Других решений у системы быть не должно.

Замечание. Уравнения системы должны быть компактными выражениями (без знаков суммирования, троеточий и т.п.), в записи которых, помимо чисел и собственно неизвестных $x$ и $y$ , разрешается использовать скобки, знак $=$ , стандартные арифметические операции и элементарные функции из школьной программы.

Показать ответ и решение

Покажем, что система

(| ----sinπx---- |{ ∘1001−-x2− y-= 0 ||( ∘--sinπy---=0 1+ y− x2

является подходящей. Обозначим систему неравенств за $A$ . Покажем, что любая пара целых чисел, удовлетворяющих $A,$ является решением.

Действительно, пусть $A$ верно, тогда каждое из подкоренных выражений числителей неотрицательно, а каждый из числителей обращается в ноль, поскольку числа $x,y$ целые.

Теперь покажем, что никакая из других пар не является решением. Пусть $(x0,y0)$ — решение, тогда $sinπx= 0,$ следовательно, $x$ — целое и $sinπy = 0$ , следовательно, $y$ — целое. Кроме этого, $1001− x2− y > 0$ , а значит, $1001− x2− y > 1$ , откуда верно первое неравенство системы $A.$ Аналогично получаем, что верно второе неравенство системы $A.$

Ответ: пример в решении

Ошибка.
Попробуйте повторить позже

Задача 6#86348

Найдите все значения параметра $a$ , при которых неравенство

∘-2----- x2+-324- 2 x + 324− f(x)≥ f(x)− a − a

имеет единственное решение, если

∘--------- f(x)= g2(x)− 400, g(x)= 19+ 2cos2x+ 4cosx.

Подсказки к задаче

Подсказка 1

Работать одновременно и с иксами, и с несколькими функциями не очень хочется. Кроме того, мы можем заметить в условии одинаковые части, например, x² + 324 и f(x) - a. Какими двумя заменами можно привести данное нам неравенство к неравенству от двух функций?

Подсказка 2

Пусть u(x) = √( x² + 324), а v(x) = f(x) – a. В какую совокупность превращается наше неравенство после преобразования, и что мы можем сказать про число решений каждого выражения в данной совокупности?

Подсказка 3

После подстановки наших функций и приведению неравенства к общему знаменателя получится неравенство, которое будет равносильно совокупности u(x) = v(x) или v(x) < 0.

Подсказка 4

Неравенство v(x) < 0 не может иметь единственного решения. Значит, наша задача сводится к тому, чтобы найти a, при которых уравнение a = f(x) - √( x² + 324) имеет единственное решение. На какой способ решения данного параметра нам могут намекнуть квадраты и косинусы в функциях?

Подсказка 5

Функции квадрата и косинуса являются чётными, значит, и f(x) - √( x² + 324) будет четной функцией. Тогда как найти a, при которых уравнение может иметь единственное решение?

Подсказка 6

Если четная функция имеет положительное решение, то она имеет и отрицательное решение, а значит, единственным решением может быть только если это x = 0. Следовательно, a = f(0) – 18 = -3. Теперь мы получили a, при котором число решений является гарантированно нечетным, но не показали, что решение единственно. Подставьте a = -3 в уравнение и докажите, что решение кроме x = 0 быть не может.

Подсказка 7

После подстановки мы получим уравнение f(x) + 3 = √( x² + 324). Решать такое уравнение мы не хотим и не умеем, какие еще способы можно применять в подобных случая?

Подсказка 8

Давайте воспользуемся методом оценки. Правая часть уравнения, очевидно, будет больше либо равна 18, а достигается данное значение при x = 0, остается только доказать, что f(x) + 3 при любых x будет не больше равно 18.

Показать ответ и решение

В обозначениях $u(x)= √x2+-324, v(x)=f(x)− a$ исходное неравенство примет вид

(u(x))2 2u(x) ≥-v(x)-+ v(x)

0≥ (u(x)−-v(x))2- v(x)

u(x)= v(x) или v(x)< 0

Функция $v(x)$ непрерывна как композиция непрерывных функций, поэтому у неравенства $v(x)< 0$ не может быть единственное решение, так что нам подходит только случай $v(x)=u(x).$ Заметим, что никакое решение этого случая не может удовлетворять $v(x)< 0,$ ведь тогда $u(x)= √x2+-324< 0,$ что невозможно.

Итак, мы переформулировали задачу и получили такую: обеспечить единственность решения уже для уравнения

∘-2----- a= f(x)− x + 324

Заметим, что функция $g(x)$ чётная, поэтому и функция $f(x)$ чётная, так что и правая часть полученного уравнения чётная. Следовательно, если уравнение имеет положительное решение, то оно имеет и отрицательное решение (и наоборот). Поэтому единственным решением может быть только $x =0.$ Сначала подставим $x =0$ и найдём, при каких $a$ это значение является решением:

√--- a= f(0)− 324= 15− 18= −3

Теперь проверим, что при $a= −3$ у уравнения

∘-2----- f(x)+ 3= x + 324

нет других решений, кроме $x =0.$ Тут уже поможет метод оценки. Правая часть не меньше $√324= 18,$ причём равенство достигается только при $x= 0.$ А вот левая часть не больше 18, потому что

∘ -2------- f(x)= g(x)− 400≤ 15,

так как

∘ ------2 |g(x)|≤ 400 +15 = 25,

ведь по неравенству треугольника

|19+ 2cos2x +4cosx|≤ |19|+ |2cos2x|+ |4cosx|≤ 19+ 2+ 4=25

Итак, при $a= −3$ действительно единственное решение, при других значениях единственность невозможна.

Ответ: -3

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#85555

Найдите все значения $a$ , при каждом из которых уравнение

x 2 |2[tga]− 1| =[tga]+ 2

имеет рациональное решение $x$ . Здесь, $[t]$ - целая часть числа $t$ .

Источники: ПВГ - 2024, 11.6 (см. pvg.mk.ru)

Показать ответ и решение

Положим $b= [tga]$ . Тогда уравнение принимает вид $(|2b− 1|)x =b2+ 2,b∈ ℤ$ . Нужно найти все целочисленные значения $b$ , при которых существует рациональное решение $x$ .

При $b= 0$ решений нет. Рассмотрим вначале случай $b> 0$ , т.е. $b∈ℕ$ . Тогда поскольку при любом натуральном $b$

2 b + 2> 2b− 1 ≥1,

то можем считать, что в представлении $x= d∕q$ числа $d$ и $q$ натуральные. Значит, числа $b2+ 2$ и $2b − 1$ имеют одни и те же простые делители.

Пусть $p$ - общий простой делитель этих чисел, тогда

{ b2+ 2= pN, 2b− 1= pM,

где $N$ и $M$ - натуральные. Исключая $b$ из левых частей уравнений этой системы, получаем

9= 4(b2 +2)− (2b− 1)(2b+1)= (4N − (2b+ 1)M )p.

Значит $(4N − (2b+1)M )$ - натуральное, а $p$ -делитель 9 , т.е. $p= 3$ . Поэтому

{ b2+ 2= pm, 2b− 1= pk,

где $m$ и $k$ - натуральные и $m > k$ . Так как

( ) ( ) 9= 4(b2+ 2)− (2b− 1)(2b+ 1)= 4⋅3m − 3k+2 ⋅3k =3k 4⋅3m−k − 3k− 2 ,

a $4⋅3m−k− 3k− 2$ не делится на 3 , то $k =2$ и $m = 3,b= 5,x= 32$ .

Для отрицательных $b$ решение проводится почти аналогично. Положим $c= −b$ . Тогда исходное уравнение будет записываться в виде:

(2c+ 1)x =c2+ 2, c∈ ℕ.

Случай $c=1$ очевиден, поскольку решение $x= 1$ . Пусть $c∈ℕ,c≥ 2$ . Аналогично предыдущему показывается, что в представлении $x= d∕q$ числа $d$ и $q$ натуральные. Опять предположив, что $p$ - общий простой делитель этих чисел, получим

{ c2+ 2= pN, 2c+ 1= pM,

и также сделаем вывод, что $p= 3$ . Поэтому

{ c2+ 2= 3m, 2c+ 1= 3k,

где $m$ и $k$ - натуральные и $m > k$ . Так как

( ) ( ) 9= 4(c2+ 2)− (2c− 1)(2c+ 1)= 4⋅3m − 3k− 2 ⋅3k =3k 4⋅3m−k − 3k+ 2 ,

а $4⋅3m−k− 3k+ 2$ не делится на 3 , то $k= 2$ и $4⋅3m−2− 32+2 =1$ или $4⋅3m−2 = 8$ , но последнее уравнение не имеет натуральных решений.

Поэтому все решения описываются уравнениями: $[tga]= −1$ и $[tga]=5$ , решив которые приходим к ответу.

Ответ:

$a ∈[−π∕4+πn;πn)∪[arctg5+ πn;arctg6+ πn),n ∈ℤ$

Ошибка.
Попробуйте повторить позже

Задача 8#85348

При каких значениях параметра $a$ неравенство

∘-2---2 2x a a − x > 9− 3 − 2

имеет хотя бы одно отрицательное решение?

Показать ответ и решение

1) $a =0$ . Тогда наше неравенство имеет вид $√−x2 > 9− 2x 3$ , которое, очевидно, решений не имеет.

2) $a⁄= 0$ . Построим графики $√-2---2 y1 = a − x$ и $2x a y2 =9 − 3 − 2$ . График $y1$ есть полуокружность с центром в точке в начале координат и радиусом $|a|.$ График $y2$ — прямая. Оба этих график представлены на рисунке:

$PIC$

Решением неравенства будут все точки, при которых график $y1$ находится выше графика $y2$ , причем, согласно условию задачи, среди решений должно быть хотя бы одно отрицательное. Это будет в том и только том случае, если прямая $y2$ будет проходить ниже точки $M (0;|a|)$ Последнее будет иметь место, если $y2(0)= 9− 2⋅30− a2 < |a|$ Итак, нам осталось решить неравенство $|a|+ a2 − 9> 0$ .

Случай 1.

{ a≥ 0 a+ a2 − 9> 0 ⇔ a >6

Случай 2

{ a≤ 0 ⇔ a< −18 a+ a2 − 9> 0

Ответ:

$a ∈(−∞;− 18)∪ (6;+∞ )$

Ошибка.
Попробуйте повторить позже

Задача 9#85236

Найдите все значения $a,$ при каждом из которых уравнение

2 (a− 3)x − 2ax+ 5a= 0

имеет решения и все решения этого уравнения положительные.

Подсказки к задаче

Подсказка 1

Подумайте, всегда ли это уравнение будет квадратным, если нет, то когда не будет?

Подсказка 2

Если перед нами точно квадратное уравнение, то необходимо гарантировать наличие корней в целом – какое условие нужно учесть для этого?

Подсказка 3

Если у квадратного уравнения есть корни, то можно расписать для них теорему Виета и подумать, какие условия нужно наложить на сумму и произведение корней, чтобы выполнялось условие задачи.

Показать ответ и решение

Данное уравнение квадратного типа и вырождается в линейное при $a= 3.$ Рассмотрим этот случай отдельно. Тогда уравнение примет вид

−2x+ 5= 0,

откуда $x =2,5> 0,$ следовательно, данное значение $a$ нам подходит.

Пусть $a ⁄= 3.$ Тогда уравнение квадратное и дискриминант

D = 4a2− 20a(a − 3)≥ 0,

откуда $a∈ [0;3,75].$

Для того, чтобы оба корня квадратного уравнения были положительны, необходимо, чтобы их сумма и произведение были положительны. Следовательно, по теореме Виета:

( || -2a-> 0 { a− 3 ||( -5a-> 0 a− 3

a∈ (3;3,75]

В ответе не забудем рассмотренный ранее случай $a= 3.$

Ответ:

$a ∈[3;3,75]$

Ошибка.
Попробуйте повторить позже

Задача 10#85235

При всех $a$ решите уравнение

2 ax +x +1 =0

Подсказки к задаче

Подсказка 1

Просят решить при всех a. Уравнение на первый взгляд квадратное, но при всех ли а?

Подсказка 2

При а = 0 получается линейное уравнение относительно х, его совсем легко решить. Пусть теперь а ≠ 0. Перед нами точно квадратное уравнение, а когда оно не имеет решений?

Подсказка 3

Когда дискриминант отрицателен! Посчитайте его и скажите, при каких а уравнение не имеет решений. А если дискриминант неотрицательный, то все мы прекрасно знаем формулу для корней уравнения. Просто выразите их!

Показать ответ и решение

При $a= 0$ уравнение примет вид $x +1= 0$ , откуда $x= −1$ .

Пусть теперь $a⁄= 0$ . Тогда уравнение является квадратным, его дискриминант $D =1− 4a$ . При $1 a ≤ 4$ дискриминант неотрицателен, поэтому

−1 ±√1-− 4a x= ----2a----

Если же $a > 14$ , то $D <0$ и уравнение не имеет корней.

Ответ:

Если $a ∈(−∞;0)∪ (0;1] 4$ , то $x= −1±√1−4a; 2a$

если $a =0$ , то $x =− 1;$

если $(1 ) a ∈ 4;+∞$ , то решений нет.

Ошибка.
Попробуйте повторить позже

Задача 11#85145

При всех значениях параметра $a$ решите уравнение

2 x +ax+ 16= 0

Показать ответ и решение

Дискриминант квадратного уравнения равен $a2− 64.$ Рассмотрим три возможных случая: дискриминант равен нулю, больше или меньше нуля.

При $2 a − 64= 0 ⇐ ⇒ a =±8$ уравнение имеет единственное решение, равное $a − 2 =±4.$

При $2 a − 64< 0 ⇐ ⇒ a ∈(−8;8)$ уравнение не имеет решений.

При $a∈ (−∞ − 8)∪ (8;+∞ )$ уравнение имеет два решения: $√ -2---- x1,2 = −-a±-a-− 64 2$

Ответ:

$x =− aпри a= ±8 2$

$−a±√a2−64- x= ----2----при a∈ (−∞ − 8)∪ (8;+∞ )$

$нет решений при a∈ (−8;8)$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#84477

Две окружности радиусов $r$ и $R$ касаются прямой $l$ в точках $A$ и $B$ . Пусть $C$ — точка пересечения этих окружностей, наиболее удалённая от $l$ . Докажите, что радиус описанной окружности треугольника $ABC$ не зависит от положения окружностей.

Показать доказательство

$PIC$

Обозначим $∠CAB$ и $∠ABC$ за $α$ и $β$ соответственно. Выберем на окружности радиуса $R$ произвольную точку $X.$ По теореме об угле между касательной и хордой

∠BXC = ∠ABC = β

По теореме синусов для треугольника $BXC$

sinB∠CBXC--=2R

BC = 2Rsin β

Аналогично для другой окружности и $AC$

AC =2rsinα

Теперь записываем теорему синусов для треугольника $ABC,$ обозначив радиус описанной окружности это треугольника за $R : ABC$

BC-- AC-- 2RABC = sinα = sinβ

2RABC = 2Rsin-β и 2RABC = 2rsinα sinα sinβ

Перемножим данные равенства

4R2 = 4rR⋅ sinα-⋅ sinβ ABC sinβ sinα

√ --- RABC = rR

Итак, $RABC$ не зависит от положения окружностей, он зависит только от их радиусов.

Ошибка.
Попробуйте повторить позже

Задача 13#84369

Найти все значения параметра $a$ , при каждом из которых из неравенства

2 x +a ≤0

следует неравенство

(x+ 2a)⋅√3-− x≤ 0

Показать ответ и решение

Первое решение.

Поймём, что данное следствие реализуется, если множество решений первого неравенства полностью содержится в множестве решений второго. Посмотрим, как выглядят эти множества решений.

Решим второе неравенство

√---- (x+ 2a)⋅ 3 − x≤ 0

⌊ 3 − x =0 || ( |⌈ { 3− x> 0 ( x+ 2a ≤0

⌊ x =3 ||| ({ ⌈ x< 3 ( x≤ −2a

x ∈{3}∪(−∞, min(3,−2a)]

Теперь рассмотрим решение первого неравенства в зависимости от $a$

x2 ≤− a

При $a> 0: x∈ ∅.$ Видно, что

∅ ∈{3}∪(−∞, −2a]

Значит, $a> 0$ подходят.

При $a= 0: x= 0.$ Видно, что

{0}∈ {3} ∪(−∞,0]

Значит, $a= 0$ подходит.

При $[ √---√--] a< 0: x∈ − −a, −a .$ Посмотрим как должны располагаться множества на числовой прямой

$PIC$

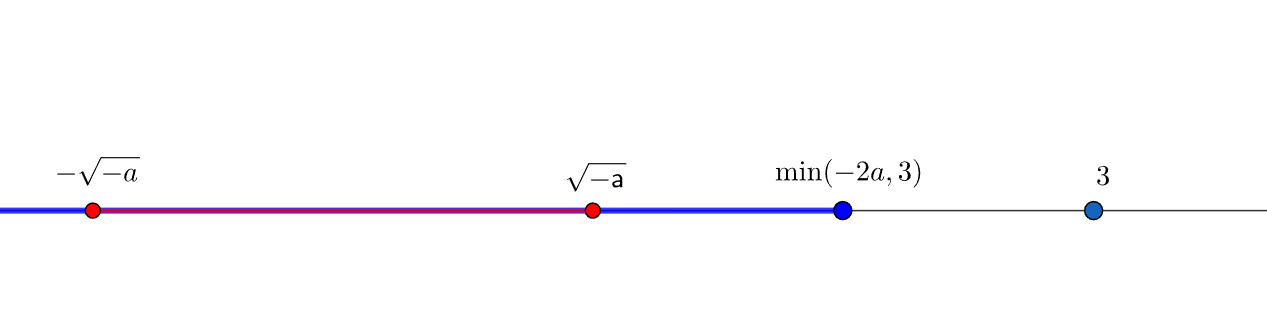
Из этого понимаем, что нужные $a$ будут удовлетворять условию

√ --- −a≤ min(3,−2a)

( { √−a-≤3 ( √--- −a ≤− 2a

Решаем систему с учётом, что $a< 0,$ получаем

({ a ≥− 9 1 ( a ≤− 4

В итоге, объединив все случаи, получаем $a∈ [−9,−0,25]∪[0,+ ∞).$ _____________________________________________

Второе решение.

Введем плоскость $xOa$ . В ней решением неравенства при конкретном $a$ будет пересечение прямой $a= a0$ с областью, которая задается неравенством. То, что одно уравнение является следствием другого, означает, что пересечение прямой $a =a0$ с множеством, задаваемым вторым неравенством, будет полностью содержать в себе пересечение прямой $a =a0$ с множеством, задаваемым первым неравенством.

Неравенство $2 x + a≤ 0$ задает область "под параболой" $2 a =− x$ .

Неравенство $√ ---- (x+ 2a) 3− x ≤0$ представим в виде равносильной совокупности:

⌊ |( 3− x= 0 ||⌈{ 3− x >0 ( x+ 2a ≤0

Эта система на плоскости представляет собой вертикальную прямую $x= 3$ и область, лежащую "ниже"прямой $a= − x2$ и "левее"c $x = 3:$

$PIC$

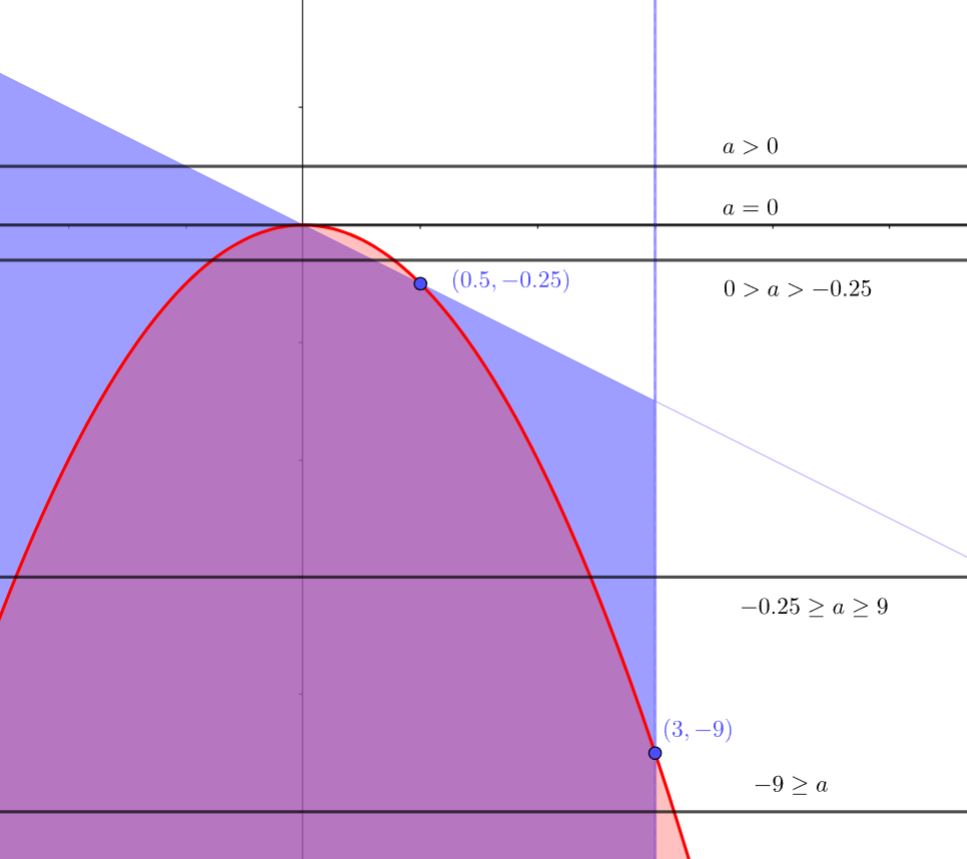
Теперь проанализируем решения неравенств при каждом $a$ .

1 случай.) $a> 0$ .

При таких значениях $a$ первое неравенство не имеет решений. Значит, любое другое неравенство будет его следствием.

2 случай.) $a= 0$ .

Решением первого неравенство будет ${0}$ , а решением второго $(−∞;0]$ . Т.е. второе неравенство является следствием первого.

3 случай.) $0> a> −0.25$ .

Как мы видим из рисунка, существуют точки "внутри"параболы, которые не принадлежат области второго неравенства. Т.е. второе неравенство не будет следствием первого.

4 случай.) $− 0.25≥ a≥ −9$ .

При таких значениях $a$ все решения первого неравенство лежат внутри множества решений второго. Т.е. второе неравенство —- следствие первого.

5 случай.) $− 9> a$ .

При таких значеиях $a$ среди решений первого неравенства есть решения $> 3$ . Но у второго неравенства таких решений быть не может. Т.е. второе неравенство не является следствием первого.

Итого получаем $a∈ [− 9;−0.25]∪[0;+ ∞)$

Ответ:

$[−9;− 0,25]∪[0;+∞ )$

Ошибка.
Попробуйте повторить позже

Задача 14#84109

При каких $a$ уравнение

7 2 2sin x= (1 +sinπa)sinx +asinx

равносильно уравнению

( 2 ) 6 2 3 (a− 1) 1+ cos x + 2sin x= 2sin x+ 2(a− 1)?

Показать ответ и решение

Заметим, что $x= 0$ является корнем первого уравнения, следовательно, при нужных значениях $a$ он будет корнем и второго уравнения. Подставив $x= 0$ во второе уравнение, получим

3 (a− 1)(1+ 1)+0= 0+ 2(a − 1)

3 (a− 1)= (a− 1)

⌊ a= 1 |⌈ a= 0 a= 2

Значит, если ситуация, описанная в задаче, и возможна, то только для данных значений $a.$ Сделаем проверку, подставив их.

Пусть $a= 1,$ тогда первое уравнение примет вид

2sin7x = sinx+ sin2x

А второе —

2sin6x = 2sin2x

Заметим, что $π x= − 2$ удовлетворяет второму уравнению. Проверим, удовлетворяет ли он первому

2⋅(−1)7 = −1+ (−1)2

−2= 0

$x= − π 2$ не является корнем первого, поэтому данное $a$ нам не подходит.

Пусть $a= 0,$ тогда первое уравнение примет вид

2sin7x =sinx

А второе —

2 6 2 −1− cos x+ 2sin x =2sin x − 2

2sin6x= 1+ sin2x− 2+1

2sin6x= sin2x

Заметим, что $4∘-1 sinx = 2$ удовлетворяет второму уравнению. Проверим, удовлетворяет ли он первому

( ∘--)7 ∘ -- 2 4 1 = 4 1 2 2

(∘ -)3 ∘ -- 4 1 = 41 2 2

$∘41- sinx= 2$ не является решением первого, поэтому данное $a$ нам не подходит.

Пусть $a= 2,$ тогда первое уравнение примет вид

7 2 2sin x= sinx +2sin x

А второе —

1+cos2 x+2sin6 x= 2sin2x+ 2

2sin6x= 2sin2x +1− cos2x

2sin6x = 3sin2x

При $sin x⁄= 0$ во втором уравнении можно поделить левую и правую часть на $sin2x,$ получим

4 2 sin x= 3

Но $sin x∈ [−1;1],$ поэтому левая часть не более 2, значит, она никак не может быть равна 3. Из этого понимаем, что решений, кроме $sinx= 0,$ быть не может.

Теперь рассмотрим первое уравнение. Докажем, что у него есть решение, отличное от $sinx= 0.$ При $sinx⁄= 0$ поделим левую и правую часть на $sin x$

2sin6x = 1+2sinx

Сделаем замену $sin x= t,$ где $t∈ [−1;1],$

2t6− 2t− 1 =0

Рассмотрим правую часть как функцию

f(t)= 2t6− 2t− 1

Она непрерывна, при этом $f(− 1) =2+ 2− 1= 3> 0$ и $f(0)= −1< 0,$ значит, на интервале $(−1,0)$ есть корень данной функции. Что и требовалось доказать.

Ответ:

$∅$

Ошибка.
Попробуйте повторить позже

Задача 15#84107

Найдите все значения $a$ , при которых истинно утверждение:

(a) для того, чтобы выполнялось неравенство $x2− 7x+ 6< 0$ , необходимо, чтобы выполнялось неравенство $|x− 3|<a$ ;

(b) для того, чтобы выполнялось неравенство $x2− 4x≤ 0$ , достаточно, чтобы выполнялось неравенство $x2− (2a +1)x+ a2 +a <0$ .

Показать ответ и решение

(a) Заметим, что $x2 − 7x+ 6= (x − 1)(x − 6),$ поэтому решения неравенства $x2 − 7x+ 6< 0$ — это $x∈ (1;6).$ Тогда $|x− 3|< a$ является необходимым условием, если его множество решений содержит $(1;6)$ (иначе найдутся такие $x,$ что неравенство $|x− 3|<a$ неверно, а условие $2 x − 7x+ 6< 0$ верно). Ясно, что $a> 0,$ иначе $|x− 3|< a$ не имеет решений. Возведем неравенство в квадрат:

(x − 3)2 < a2

Перенесем $a2$ влево и разложим по разности квадратов:

(x− 3− a)(x− 3+a)< 0

Тогда решения этого неравенства — это $x∈ (3− a;3+a),$ так как $a> 0.$ Так как это множество должно содержать $(1;6),$ то получаем систему неравенств:

{ 3 − a≤ 13+ a≥ 6

Решаем оба неравенства

{ a≥ 2a≥ 3

Решения этой системы: $a ∈[3;+ ∞)$

(b) Так как $2 x − 4x= x(x − 4),$ то неравенство $2 x − 4x≤ 0$ имеет множество решений $[0;4].$

Условие $2 2 x − (2a+ 1)x+a + a< 0$ является достаточным для $2 x − 4x≤ 0,$ если его множество решений содержится в множестве $[0;4].$

Заметим, что

x2− (2a +1)x+ a2 +a =x2− (a+(a+ 1))x+ a(a +1)

Тогда по теореме Виета корни этого квадратного трехчлена $x1 = a$ и $x2 =a +1.$ Тогда решения неравенства $2 2 x − (2a+ 1)x+a + a< 0$ — это $x∈ (a;a+ 1).$ Так как это множество должно содержаться в $[0;4]$ имеем систему

{ a≥ 0a+1 ≤4

Тогда получаем $0≤ a≤ 3,$ то есть $a ∈[0;3].$

Ответ:

(a) $a∈ [3;+∞ );$

(b) $a∈[0;3].$

Ошибка.
Попробуйте повторить позже

Задача 16#84106

Найдите все пары $(a,b)$ такие, что любая пара $(x,y)$ , удовлетворяющая уравнению

x y = a,

удовлетворяет уравнению

(x+y)2 = b.

Показать ответ и решение

Исходя из условий, нам нужно подобрать такие $(a,b),$ чтобы

x 2 y = a =⇒ (x +y) = b

Значит, при подходящих $(a,b)$ второе равенство в частности должно быть верно для точек $(a,1)$ и $(2a,2),$ т.к. они удовлетворяют первому равенству, подставив их, получим систему

{ (a+ 1)2 = b (2a+ 2)2 = b

{ 2 (a+ 1)=2 b 4(a+ 1) = b

Следовательно,

4b= b ⇐ ⇒ b =0

Подставив значение $b$ в первое уравнение системы, получим

(a+ 1)2 = 0

a= −1

Мы показали, что если ситуация, описанная в задаче, и возможна, то только для $a= −1,b= 0.$ Проверим

x 2 y =− 1 =⇒ (x+ y) =0

Подходит. Значит, $(− 1,0)$ — ответ.

Ответ:

$(−1,0)$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#84105

Даны три утверждения:

(a) уравнение $x +x1= a$ не имеет корней;

(b) справедливо равенство $√--------- a2− 4a+ 4= 2− a;$

При каких $a$ два из утверждений (a)–(c) истинны, а одно ложно?

Показать ответ и решение

Найдём сначала подходящие значения $a$ для каждого утверждения по отдельности.

_________________________________________________________________________________________________________________________________________________________________________________

(a) Пусть $x ⁄=0,$ тогда

x2− ax +1 =0

Заметим, что $x= 0$ точно не является корнем данного уравнения, поэтому проверка после нахождения корней не нужна. Квадратное уравнение не имеет корней, когда дискриминант отрицателен, тогда

D = a2 − 4< 0

a∈(−2;2)

_________________________________________________________________________________________________________________________________________________________________________________

(b) Выделим полный квадрат в подкоренной выражении

∘ ------ (a− 2)2 =2 − a

|a− 2|= 2− a

Значит, нужно, чтобы модуль либо был равен 0, либо раскрылся со знаком минус. Это происходит в случае

a− 2≤ 0

a ∈(−∞;2]

_________________________________________________________________________________________________________________________________________________________________________________

(c) Заметим, что $(−y)2 = y2$ и $sin2(−y)= sin2(y).$ Значит, если $(x0,y0)$ является решением данной системы, тогда $(x0,−y0)$ тоже является решением. Следовательно, чтобы решение было единственно, то данные решения должны совпадать, а это возможно только, когда $y0 = 0.$ Подставим это значение в исходную систему

{ x= a =⇒ a= −3 x= −3

Теперь мы поняли, что все $a,$ кроме $a= −3,$ нам не подходят. Осталось сделать проверку для $a= −3.$

{ x+y2 = −3 x− sin2y =− 3

{ 2 x+ 3= −y2 x+ 3= sin y

Из первого уравнения видно, что $x+ 3≤ 0,$ а из второго видно, что $x +3 ≥0.$ Следовательно, $x =−3.$ Подставив $x$ в систему, получим $y = 0.$ Значит, $(3,0)$ будет единственным решением, т.е. $a= −3$ подходит.

_________________________________________________________________________________________________________________________________________________________________________________

Теперь отметим на числовой прямой, когда верно каждое из утверждений.

$PIC$

Видно, что под условия задачи подходят $a∈ {− 3} ∪(−2;2).$

Ответ:

${−3}∪ (− 2;2)$

Ошибка.
Попробуйте повторить позже

Задача 18#84104

Даны высказывания:

A := число x является реш ением неравенства x− 1< 0, 2 B := число x является реш ением неравенства x − 1< 0.

Являются ли эти высказывания эквивалентными? Какое из них является необходимым условием для другого (а какое — достаточным)? Какое из этих неравенств естественно считать следствием другого неравенства?

Показать ответ и решение

Так как неравенство из утверждения $A$ имеет множество решений $(−∞; 1),$ а неравенство из утверждения $B$ имеет множество решений $(−1;1),$ и эти множества не совпадают, то неравенства не эквивалентны.

Так как $(−1;1)⊂ (−∞;1),$ то из $B$ следует $A$ (то есть для любого $x,$ удовлетворяющего $B,$ верно $A;$ заметим, что наоборот это неверно).

Ответ:

неэквивалентны, из $B$ следует $A.$

Ошибка.
Попробуйте повторить позже

Задача 19#83309

Область $G$ на плоскости, ограниченная двумя параболами $y =− 2x2 +3x$ и $y = x2+ px +q,$ имеет площадь 32. Вертикальная прямая $x =1$ разбивает её на две равновеликие части. Найти $p$ и $q$ .

Подсказки к задаче

Подсказка 1

Площади, графики, да тут всё намекает на определённый интеграл, а чтобы его найти надо посмотреть на модуль разности графиков, именно модуль, потому что площадь должна быть не отрицательной!

Подсказка 2

Нам сказано, что прямая x = 1 разбивает график на 2 равновеликие части, а парабола сама по себе фигура довольно симметричная, не можем ли мы что-то сказать про точку x = 1 для параболы?

Подсказка 3

Верно, это абсцисса вершины параболы, а мы умеем находить её через коэффициенты параболы, остаётся только посчитать определённый интеграл и получить условие на q, и задача будет уничтожена!

Показать ответ и решение

Обозначим данные параболы $y(x)= −2x2+3x 1$ и $y (x)= x2+ px+ q, 2$ пусть они пересекаются в точках с абсциссами $x1 < x2.$

Ограниченная ими площадь (над одним графиком и под другим) равна модулю разности площадей под графиками на отрезке $[x1,x2].$ А это по формуле Ньютона-Лейбница считается как

||∫ x2 ∫ x2 || ||∫ x2( 2 ) || || x1 y1(x)dx− x1 y2(x)dx||= ||x1 3x + (p − 3)x+ qdx||

Заметим, что полученный интеграл равен площади под графиком параболы $3x2+(p− 3)x+ q$ на отрезке $[x1,x2]$ . По условию прямая $x =1$ делит эту площадь на две равновеликие. Значит, $x= 1$ — абсцисса вершины этой параболы. С одной стороны, она равна $3−6p,$ а с другой стороны, $x1+2x2= 1.$ Тогда находим

3−-p =1 =⇒ p= −3 6

Теперь запишем данное в условии значение площади и получим уравнение на оставшийся параметр:

| | 32= ||∫ x2(3x2− 6x+ q)dx||=||(x3− x3− 3(x2 − x2)+q(x − x))||= |x1 | 2 1 2 1 2 1

| | | | = |(x2− x1)(x21 +x22+ x1x2 − 3x1− 3x2 +q)|=|(x2 − x1)((x1+x2)2− x1x2− 3(x1+ x2)+q)|=

|| 2q|| |||∘---4q 2q||| (∘ ---q)3 = ||(x2− x1)(−2+ 3-)||= || 4− -3 (2− 3-)||= 4 1− 3

(∘---q)3 8= 1 −3

q 4= 1− 3

q = −9

Ответ:

$p =−3,q = −9$

Ошибка.
Попробуйте повторить позже

Задача 20#81380

При каких значениях параметра $b$ существует прямая, касающаяся графика функции $f(x)=x4+ bx2+x$ в двух точках? Для каждого такого значения параметра $b$ найдите уравнение соответствующей прямой.

Источники: Миссия выполнима - 2024, 11.7 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Что означает касание? Какую систему нам нужно решать? Сколько корней у неё должно быть?

Показать ответ и решение

Условие, что прямая вида $y =kx+ m$ касается графика $y = f(x)$ означает равенство функций и равенство производных в точке касания:

({ 4 2 x + bx +x =kx+ m (4x3+ 2bx+ 1= k

Нас интересует, когда эта система имеет ровно $2$ корня. Заметим, что система эквивалентна

( { x4 +bx2 = (k − 1)x+ m ( 4x3+ 2bx= k− 1

То есть должна существовать прямая $y =(k− 1)x +m$ , которая касается графика $y = x4+ bx2$ .

При $b≥ 0$ ее производная $4x3+ 2bx$ монотонная функция, а значит, $4x3+ 2bx= k− 1$ имеет не более одного решения, тогда и вся система имеет не более одного решения.

При $b< 0$ можно заметить, что касательные в точках локального минимума $∘--- x1,2 =± −-b 2$ (нашли их как корни производной $3 4x + 2bx =0$ ) имеют одинаковый коэффициент наклона $0$ , а также в этих точках значение функции совпадает в силу чётности. Тогда прямая $b2 b2 b2 y =x41+ bx21 = 4-− 2-= −4$ будет касательной сразу к двум точкам (только к двум точкам, потому что в точке $x= 0$ касательная $y = 0$ ; в других же точках коэффициент наклона касательной не $0$ ).