Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведены высоты
и
Докажите, что углы
и
равны.
Треугольник остроугольный по условию, значит, точки
и
лежат на сторонах
и
соответственно.
![]()
Рассмотрим четырехугольник Заметим, что углы
и
являются прямыми и опираются на одну и ту
же сторону — сторону
значит, четырехугольник
является вписанным. Тогда углы, опирающиеся на дугу
равны, то есть
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведены высоты
и
Докажите,
что углы
и
равны.
Способ 1.
Так как и
— высоты, то:
Обозначим точку пересечения и
за
— остроугольный,
поэтому точка пересечения высот лежит внутри треугольника.
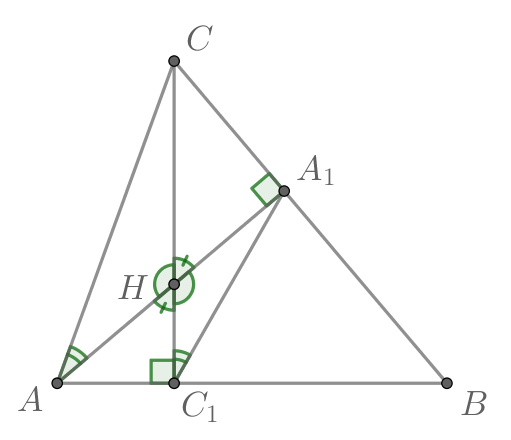
Рассмотрим и
- 1.
- 2.
как вертикальные углы.
по двум углам.
Запишем коэффициент подобия:
Рассмотрим и
- 1.
как вертикальные углы;
- 2.
из подобия
и
по двум сторонам и углу между ними. Тогда:
как соответственные углы подобных треугольников.
Так как
то
Способ 2.
Так как и
— высоты, то
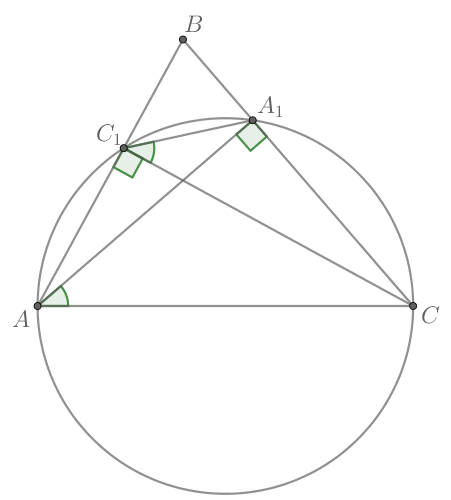
Так как и оба угла опираются на отрезок
то
четырехугольник
— вписанный.
Следовательно, как вписанные углы, опирающиеся на дугу
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Высоты и
остроугольного треугольника
пересекаются в точке
Докажите, что углы
и
равны.
Так как и
— высоты, то:
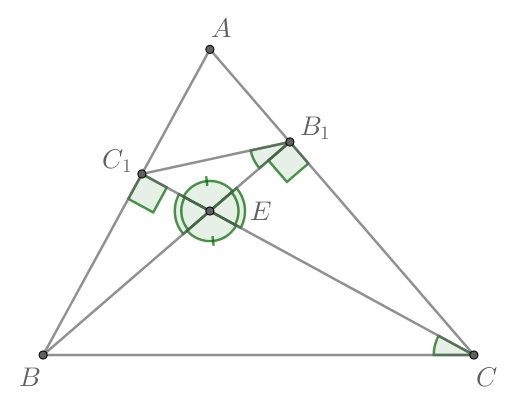
Рассмотрим треугольники и
Так как
как вертикальные, то треугольники
и
подобны
по двум углам.
Запишем отношение подобия:
Рассмотрим треугольники и
- 1.
как вертикальные;
- 2.
Тогда треугольники и
подобны по двум сторонам и углу между
ними.
как соответственные углы подобных треугольников.
Значит,
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Высоты и
остроугольного треугольника
пересекаются в точке
Докажите, что углы
и
равны.
Так как и
— высоты, то
При этом
и
опираются на один отрезок
Значит, по признаку вписанного
четырёхугольника около четырёхугольника
можно описать окружность.
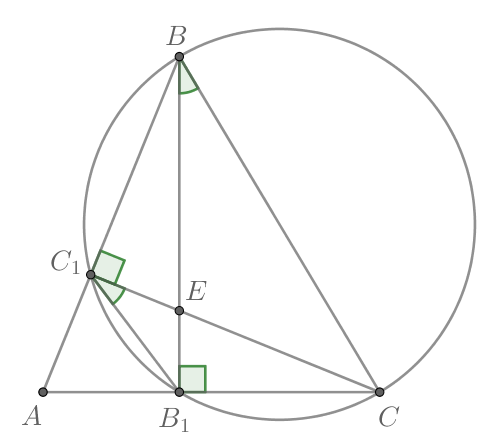
Так как вписанные углы, опирающиеся на одну и ту же дугу, равны, а
и
опираются на дугу
то
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В треугольнике с тупым углом
проведены высоты
и
Докажите, что треугольники
и
подобны.
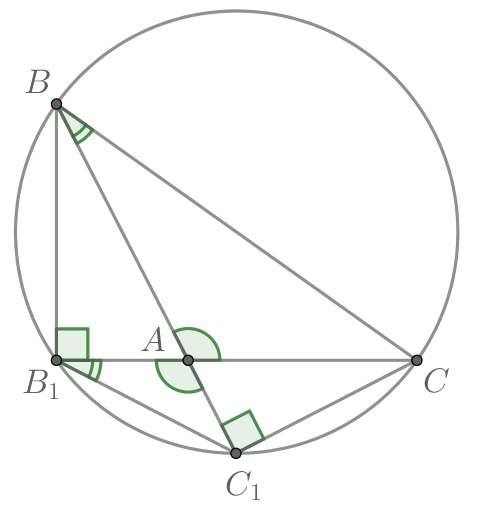
Так как и
— высоты, то
и
опираются на один отрезок
и равны, поэтому по признаку
вписанного четырёхугольника
— вписанный.
и
вписанные и опираются на одну дугу
Тогда
Рассмотрим треугольники и
как
вертикальные,
Тогда треугольники
и
подобны
по двум углам.
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В треугольнике с тупым углом
проведены высоты
и
Докажите, что треугольники
и
подобны.
Способ 1.
Так как — тупой, то точки
и
лежат на продолжении сторон
и
соответственно.
Так как и
— высоты, то
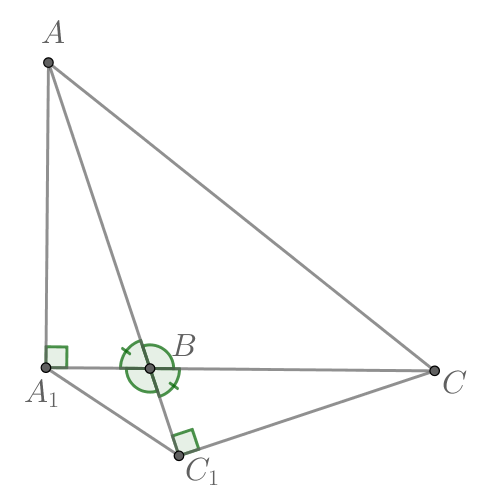
Рассмотрим и
- 1.
- 2.
как вертикальные углы.
по двум углам.
Запишем коэффициент подобия:
Рассмотрим и
- 1.
как вертикальные углы;
- 2.
из подобия
и
по двум сторонам и углу между ними.
Способ 2.
и
опираются на отрезок
и
Тогда около четырёхугольника
можно описать окружность.
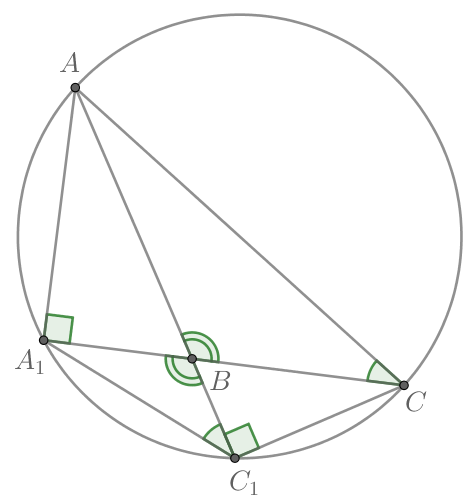
так как они вписанные и опираются на дугу
Рассмотрим треугольники и
Так как
как вертикальные. Тогда
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В треугольнике известны длины сторон
точка
—
центр окружности, описанной около треугольника
Прямая
перпендикулярная прямой
пересекает сторону
в точке
Найдите
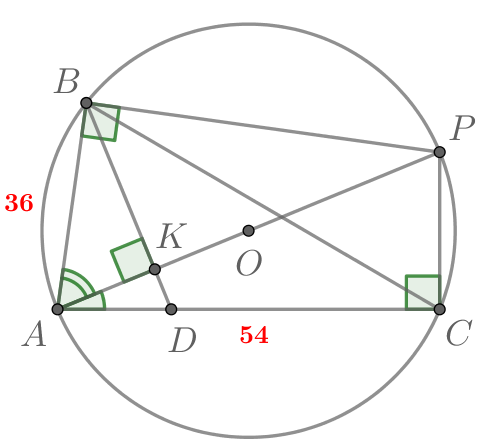
Продлим до пересечения с описанной окружностью треугольника
Обозначим полученную точку за
Проведём
и
— диаметр описанной около треугольника
окружности, поэтому
так как они опираются на диаметр.
Обозначим точку пересечения с
за
Треугольники и
подобны по двум углам (
— общий,
). Запишем отношение подобия:
Рассмотрим треугольники и
Они подобны по двум углам (
—
общий,
). Запишем отношение подобия:
Получили:
Тогда
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
На стороне треугольника
отмечены точки
и
так, что
Докажите, что если
то
Рассмотрим треугольник Если в нем
то он равнобедренный. Тогда углы при его основании
равны, то
есть
Углы, смежные равным, равны, значит,
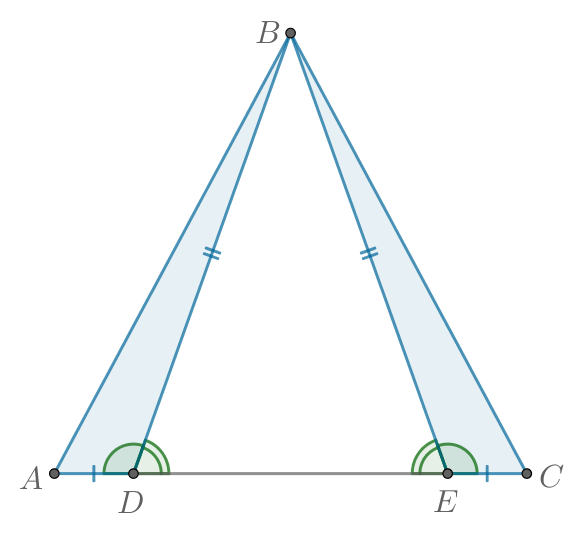
Рассмотрим треугольники и
В них
и
по условию, и
значит, эти
треугольники равны по двум сторонам и углу между ними. В равных треугольниках соответственные элементы равны,
следовательно,
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В равностороннем треугольнике точки
— середины сторон
соответственно. Докажите, что
треугольник
— равносторонний.
Способ 1
По условию
и
— середины сторон
соответственно. Тогда
и
— средние линии
треугольника
Значит,
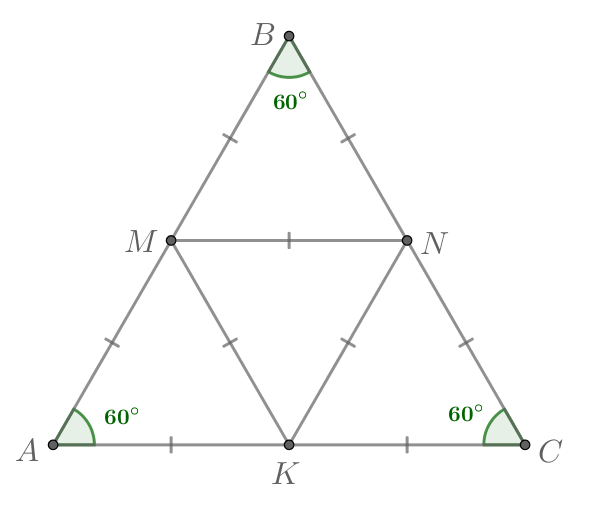
Так как — равносторонний треугольник, в нем
следовательно,
Значит,
треугольник
является равносторонним.
Способ 2
Треугольник — равносторонний, значит,
Также
Рассмотрим треугольники и
Они равны по первому признаку равенства треугольников, так как
и
Аналогично равны треугольники
и
и
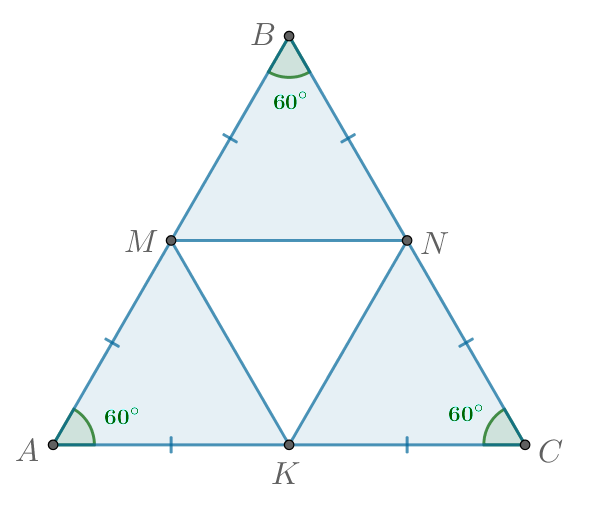
В равных треугольниках соответственные элементы равны, следовательно, Значит, треугольник
является равносторонним.
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |



