Планиметрия на Энергетике —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Планиметрия на Энергетике

Тема Надежда энергетики

Планиметрия на Энергетике

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела надежда энергетики

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#87531

В круговой сектор радиуса $R$ с центральным углом $α$ $(0< α≤ π∕2)$ вписаны две окружности (обе касаются радиусов-сторон сектора, друг друга внешним образом, а большая касается окружности сектора). Какую наибольшую долю может составлять расстояние между центрами вписанных окружностей от величины $R$ и при каком значении $α$ это достигается?

Показать ответ и решение

Обозначим радиусы малой и большой вписанных окружностей через $x$ и $y$ , введём величину $β = α 2$ . Отметим, что $π 0 <β < 4$ .

$PIC$

Выразим стороны треугольника через радиусы трёх окружностей.

OO2 = R − y, OO1 = R− x− 2y

Из подобия прямоугольных треугольников получаем

--1-= R-− y-= R−-x−-2y sin β y x

Откуда

R-= R-− 2x y x

-x y- y- R = (1− 2⋅R)⋅R

Расстояние между центрами вписанных окружностей $O1O2$ равно $x+y$ .

Рассмотрим искомое отношение

x +y y y y y y --R- = (1− 2R)R-+ R-= 2(1− R)R-

Относительно величины $t= yR-$ это отношение есть парабола $2t(t− 1)$ . Выразим параметр $t$ через угол $β$ .

si1nβ = Ry − 1

t= y= --sinβ--= ---1--- R 1 +sinβ 1+ s1inβ

Таким образом, при изменении $β$ от $0$ до $π 4$ параметр $t$ растёт от $0$ до $√ - 2− 1$ . Остаётся найти максимум параболы $2t(1− t)$ на полученном отрезке $√- [0; 2− 1]$ . Вершина параболы лежит правее отрезка, следовательно искомый максимум достигается при $√- t= t0 = 2− 1$ и равен $√ - 2(3 2− 4)$ .

Ответ:

$2(3√2-− 4)$ при $α= π 2$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#76463

На каждой из сторон параллелограмма выбрано по произвольной точке. Точки на соседних сторонах параллелограмма соединены отрезками прямых. В результате от параллелограмма оказываются отсеченными четыре треугольника. Вокруг каждого из этих треугольников описана окружность. Докажите, что центры этих окружностей являются вершинами некоторого параллелограмма.

Источники: Надежда энергетики-2022, 11.4 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Взглянув на условие, кажется, что надо доказать что-то страшное и непонятно, как это делать. Но давайте вспомним, какие в принципе у нас есть способы решения задач по планиметрии? Углы считать мы не пойдём, в лоб доказывать равенство сторон тоже. Как можно сделать это хитрее?

Показать доказательство

Изобразим окружности и их центры, которые обозначим $O ,...,O . 1 4$ Рассмотрим векторы $O O ,O O 1 2 4 3$ и $O O ,O O . 1 4 2 3$

$PIC$

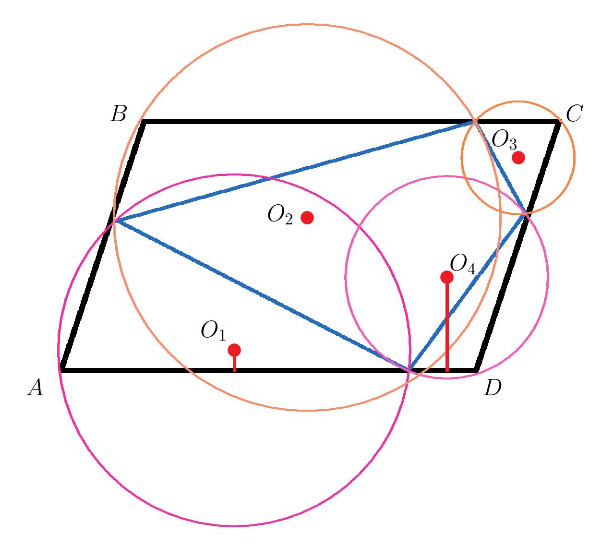
Поскольку центры описанных окружностей лежат на пересечении серединных перпендикуляров, проекции указанных векторов на стороны исходного параллелограмма будут равны половине этих сторон.

Таким образом, если ввести две оси: одну параллельно стороне $AB,$ а другую параллельно стороне $AD,$ то каждая пара рассматриваемых векторов будет иметь одинаковые проекции на каждую из введенных осей. Отсюда следует попарное равенство самих векторов.

Ошибка.
Попробуйте повторить позже

Задача 3#88170

Две равные окружности пересекаются в точках $P$ и $Q$ . Произвольная прямая, проходящая через $Q$ , повторно пересекает окружности в точках $A$ и $B$ , а касательные к окружности в этих точках пересекаются в точке $C$ . Докажите, что отрезки $AQ$ и $CB$ видны из точки $P$ под одинаковыми углами.

Подсказки к задаче

Подсказка 1

Доказать, что отрезки видны под равными углами из точки Р равносильно равенству углов APQ и CPB. Чему можно приравнять углы APQ и QPB?

Подсказка 2

Углы APQ и QAC равны, поэтому осталось показать равенство углов САВ и СРВ. О чём говорит равенство САВ и СРВ?

Подсказка 3

Да, оно равносильно вписанности четырёхугольника CAPB. Чтобы доказать это, воспользуемся признаком вписанности, использующим сумму двух противоположных углов!

Показать доказательство

$PIC$