Надежда энергетики —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Надежда энергетики

Тема Надежда энергетики

Надежда энергетики

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Разделы подтемы Надежда энергетики

Логика на Энергетике

Комбинаторика + комбигео на Энергетике

Алгебраические текстовые задачи на Энергетике

Оптимизация на Энергетике

Многочлены на Энергетике

Уравнения с целой и дробной частями на Энергетике

Теория чисел на Энергетике

Планиметрия на Энергетике

Стереометрия на Энергетике

Подтемы раздела надежда энергетики

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#87532

Коэффициенты многочлена степени $n> 2024$

n n−1 Pn(x)= anx + an−1x + ...+ a1x +a0,

взятые в том же порядке (начиная со старшей степени), образуют геометрическую прогрессию со знаменателем $q$ $(q ⁄= 0,±1 ).$ Выясните, может ли $Pn(x)$ иметь только один корень.

Если может, укажите минимальную степень (из диапазона выше), при которой это возможно, и выразите корень через $a 0$ и $q$ . Если нет, укажите минимально возможное количество корней при любом $n> 2024.$

Показать ответ и решение

Заметим, что $a ⁄= 0 n$ и $a ⁄=0, 0$ следовательно $a = a qn ⁄= 0. 0 n$ Значит, $x= 0$ не является корнем.

Поймём, что одночлены (начиная со старшего) в многочлене образуют геометрическую прогрессию с знаменателем $q x.$ Значит, многочлен может быть представлен как сумма первых $n+ 1$ члена данной прогрессии. Заметим, что если $x= q,$ то

n n−1 n n n Pn(q)= anq +an−1q + ...+a1q+ a0 = an = a◟nq-+anq◝+◜-...+-anq◞ n+1раз

n n Pn(q)= anq (n +1)⁄= 0, т.к. a ⁄= 0,q ⁄=0

Значит, $x= q$ не корень. Поэтому дальше будем считать $x ⁄=q$ и запишем следующее

anxn((q)n+1− 1) Pn(x)= anxn +an−1xn−1+ ...+ a1x+ a0 =------xq-------- x − 1

Выразим корни с учётом $x⁄= 0$ и $an ⁄= 0$

anxn((q)n+1 − 1) -----qx--------=0 x − 1

( ) ( q n+1− 1= 0 x

xn+1 = qn+1

Если $n+ 1$ нечётно, тогда $x =q,$ чего быть не может, а если $n+ 1$ чётно, тогда $x= ±q,$ а в силу ограничений получаем $x= −q.$ Это и будет единственным корнем.

Теперь найдём минимальное $n.$ Из условий $n > 2024$ и $n+ 1$ чётно получаем, что $n= 2025$ подходит.

Ответ:

может при $n = 2025 min$ , корень равен $− q$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#87531

В круговой сектор радиуса $R$ с центральным углом $α$ $(0< α≤ π∕2)$ вписаны две окружности (обе касаются радиусов-сторон сектора, друг друга внешним образом, а большая касается окружности сектора). Какую наибольшую долю может составлять расстояние между центрами вписанных окружностей от величины $R$ и при каком значении $α$ это достигается?

Показать ответ и решение

Обозначим радиусы малой и большой вписанных окружностей через $x$ и $y$ , введём величину $β = α 2$ . Отметим, что $π 0 <β < 4$ .

$PIC$

Выразим стороны треугольника через радиусы трёх окружностей.

OO2 = R − y, OO1 = R− x− 2y

Из подобия прямоугольных треугольников получаем

--1-= R-− y-= R−-x−-2y sin β y x

Откуда

R-= R-− 2x y x

-x y- y- R = (1− 2⋅R)⋅R

Расстояние между центрами вписанных окружностей $O1O2$ равно $x+y$ .

Рассмотрим искомое отношение

x +y y y y y y --R- = (1− 2R)R-+ R-= 2(1− R)R-

Относительно величины $t= yR-$ это отношение есть парабола $2t(t− 1)$ . Выразим параметр $t$ через угол $β$ .

si1nβ = Ry − 1

t= y= --sinβ--= ---1--- R 1 +sinβ 1+ s1inβ

Таким образом, при изменении $β$ от $0$ до $π 4$ параметр $t$ растёт от $0$ до $√ - 2− 1$ . Остаётся найти максимум параболы $2t(1− t)$ на полученном отрезке $√- [0; 2− 1]$ . Вершина параболы лежит правее отрезка, следовательно искомый максимум достигается при $√- t= t0 = 2− 1$ и равен $√ - 2(3 2− 4)$ .

Ответ:

$2(3√2-− 4)$ при $α= π 2$

Ошибка.
Попробуйте повторить позже

Задача 3#87530

Запись числа $A$ заканчивается цифрой 3. Если же последнюю цифру переставить в начало, то получится число, на 27 больше $A$ . Найдите $A$ , если известно, что оно делится на 99, или докажите, что такого числа не существует.

Показать ответ и решение

Пусть $A$ имеет в своей записи $k+ 1$ цифру, тогда

A= x⋅10+ 3

где $x$ — это какое-то $k$ -значное число. Значит, после перестановки 3 в начало мы получим число

B = 3⋅10k+ x

По условию $B =A + 27,$ получаем равенство

10x+ 3+ 27 =3 ⋅10k+ x

9x= 3⋅10k− 30 =30⋅(10k−1− 1)= 30 ⋅ 9◟9.◝..◜9 ◞ k−1цифр

x =30⋅ 1◟1.◝◜..1◞ = 3◟3..◝.◜30◞ k−1цифр k цифр

Следовательно, можем понять как выглядит $A$

A= 3◟3..◝◜.3◞ 03 k−1цифр

По условию $A$ должно делиться на 99, а следовательно оно делиться на 11. Значит, по признаку делимости на 11, знакопеременная сумма цифр числа $A$ должна делиться на 11. Но видно из его записи, когда $k − 1$ чётно, то знакопеременная сумма равна 3, когда $k− 1$ нечётно, то знакопеременная сумма равна 6. Следовательно, на 11 $A$ делиться не может.

В итоге делаем вывод, что чисел, подходящих под условия задачи, не существует.

Ответ: нет

Ошибка.
Попробуйте повторить позже

Задача 4#87529

На каждой из двух прямолинейных линий электропередач установлены обслуживающие подстанции. На линии А — через каждые $m$ км, на линии В — через каждые $q$ км. Если занумеровать их подряд вдоль каждой линии, то расстояния между подстанциями $A1$ и $B1$ равно $√- 15 2$ км, между $A3$ и $B3$ равно $√-- 5 34$ км, между $A4$ и $B4$ равно $√-- 15 10$ км. Определите, параллельны ли данные линии? Если да, то найдите расстояние между ними. Если нет, то найдите расстояние от подстанции $A1$ до точки их пересечения.

Показать ответ и решение

Если ввести декартову систему координат с началом в точке $A 1$ и одной из осей, направленной вдоль линии $A$ (можно и иначе), то координаты всех подстанций будут изменяться линейным образом, следовательно, квадраты расстояний $AkBk$ будут являться значениями некоторого многочлена второй степени $2 P(s)= as + bs+ c$ . Найдём его. Будем измерять $s$ в условных единицах длины, так что каждая следующая единица соответствует следующей паре подстанций. Тогда

2 P (0)= c= A1B1 = 9⋅50

2 P (2)= 4a+ 2b+ c= A3B3 = 17⋅50

2 P (3)= 9a+ 3b+ c= A4B4 = 45⋅50

Для простоты расчетов уменьшим все правые части в $50$ раз и из полученной линейной системы найдём

a= 8,b =− 12,c= 9.

Следовательно, искомый многочлен имеет вид

P(s)= 50(8s2− 12s+ 9)

Его дискриминант отрицателен, $P(s)$ нигде не обращается в ноль (и всюду положителен). Следовательно, линии не пересекаются. Квадрат расстояния между ними равен минимальному значению $P (s)$ , которое достигается при $s =s0 = 34$ и равно $50⋅ 92 = 225$ . А само расстояние равно 15.

Ответ:

Линии параллельны, расстояние между ними равно $15$ км.

Ошибка.
Попробуйте повторить позже

Задача 5#87528

Госпожа Такаято решила сесть на диету и из каждых десяти дней делать четыре голодных и шесть обжорных. Сколькими разными способами она может распределить такие дни, чтобы у неё не было более двух голодных дней подряд (в рамках одной десятидневки)?

Показать ответ и решение

Посчитаем сначала общее количество способов распределить дни без учёта условия. Заметим, что нам нужно выбрать 4 голодных дня, остальные сразу станут обжорными. Значит, их количество

4 10⋅9⋅8⋅7 C10 =---4!---= 210

Теперь посчитаем способы, которые нам не подходят под условия, чтобы вычесть их. Понятно, чтобы не выполнялось условие задачи нужно иметь хотя бы 3 голодных дня подряд, но, т.к. голодных дней всего 4 возможно два варианта:

1) У нас 3 голодных дня подряд и 1 голодный, не стоящий с ними рядом. Будем воспринимать эти 3 дня как 1, назовём его большой голодный день, т.е. теперь у нас будет 8 дней и мы распределяем большой голодный день и голодный день так, чтобы они не стояли рядом. Если большой голодный стоит первым или последним, то у обычного есть 6 вариантов, в иных случаях у него их 5. В итоге

2⋅6+ 6⋅5= 42

2) У нас 4 голодных дня подряд. Количество таких способов равно количеству способов выбрать место для первого голодного дня, оно равно 7.

В итоге количество способов распределения, подходящих под условия равно

210 − 42− 7= 161

Ответ: 161

Ошибка.
Попробуйте повторить позже

Задача 6#71018

Какое число больше: $20232023$ или $20222024?$

Источники: Надежда энергетики-2023, 11.5 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Есть два способа определить какое из двух чисел больше. Можно вычесть одно из второго и посмотреть на знак, а можно найти отношение первого ко второму и посмотреть больше оно единицы или меньше. Очевидно, что вычитание в этой задаче нам ничего не даст, поэтому давайте найдем отношение.

Подсказка 2

Подумайте, как стоит расписать полученное отношение, чтобы воспользоваться тем, что для всех натуральных k выполняется неравенство 2 <= (1 + 1/k)^k < 3

Показать ответ и решение

Рассмотрим отношение чисел

20232023 2023 ( 2023)2022 2023 ( 1 )2022 20222024 = 20222-⋅ 2022 = 20222 ⋅ 1 +2022

Применим известное неравенство:

( ) 2 < 1+ 1 k < 3 ∀k ∈ℕ, k> 1 k

Тогда

2023 ( 1 )2022 2023⋅3 20222 ⋅ 1+ 2022 < 2022-⋅2022 < 1

_________________________________________________________________________________________________________________________________________________________________________________

Замечание.

Известное неравенство принималось на олимпиаде без док-ва, но любые корректные попытки его обоснования поощрялись. Покажем, как его можно доказать с помощью формулы бинома Ньютона:

( ) 1 +-1 k = 1+ n-⋅ 1+ n(n−-1)⋅ 1-+ n(n−-1)(n−-2)-⋅ 1-+ ...+ n!⋅ 1-= k 1! n 2! n2 3! n3 n! nn

1- ( 1) -1 ( 1) ( 2) 1-( 1) ( n−-1) = 2+ 2! ⋅ 1− n +3! ⋅ 1− n 1− n + ...+ n! 1− n ⋅...⋅ 1− n

Видно, что все скобки вида $( k) 1+ n$ меньше 1, но при этом больше 0. Значит, если заменим их на 1, то выражение от этого увеличиться.

( ) ( )( ) ( ) ( ) 2+ 1-⋅ 1− 1 + 1-⋅ 1− 1 1 −-2 + ...+ 1- 1− 1 ⋅...⋅ 1− n−-1 < 2! n 3! n n n! n n

<2 + 1--+ --1--+ ...+ ---1----< 2+ 1 +-1 +...+--1- 1⋅2 1⋅2⋅3 1⋅2⋅...⋅n 2 22 2n−1

Последнее неравенство верно, ведь мы просто заменили в числителях все числа, которые больше 2, на 2, тем самым уменьшили знаменатели, следовательно, увеличили значение выражения.

1 -1 --1- 1 -1 --1- -1 1 -1-- 2+ 2 + 22 + ...+ 2n−1 < 2+ 2 +22 +...+ 2n−1 + 2n +...=2 +2 ⋅1− 12 = 3

В конце мы воспользовались формулой суммы бесконечно убывающей геометрической прогрессии.

Ответ:

$20222024$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#71017

Две сферы касаются друг друга внешним образом и каждая из них касается внутренним образом большей сферы. Радиус одной в два раза, а другой — в три раза меньше радиуса наибольшей сферы. В точке касания малых сфер друг с другом построена касательная плоскость к ним. Найдите расстояние от этой плоскости до центра наибольшей сферы, если ее радиус равен $R.$

Источники: Надежда энергетики-2023, 11.4 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Не очень удобно работать в пространстве. Может, тогда перейти в плоскость? Давайте перейдем в плоскость α, проходящую через центры наших сфер...

Подсказка 2

Обозначим их центры за O, O₁ и O₂. Пускай R=6r ⇒ радиусы оставшихся двух сфер равны 3r и 2r ⇒ O₁O₂=5r, OO₁=3r и OO₂=4r. Что мы можем сказать про треугольник △O₁OO₂?

Подсказка 3

Верно, он прямоугольный! Пускай плоскость β, касающаяся наших сфер, пересекает α по прямой L. Обозначим за K- точку пересечения OO₂ и L, D- основание перпендикуляра из O на прямую L и F- точку касания маленьких сфер. Какие между собой треугольники △ODK, △KFO₂ и △O₁OO₂?

Подсказка 4

В яблочко, они подобны! Тогда: KO₂/FO₂=O₁O₂/OO₂ ⇒ KO₂=r*5/2 ⇒ KO=r*3/2. Также: OD/KO=OO₂/O₁O₂ ⇒ OD=r*6/5=R/5.

Показать ответ и решение

Проведём сечение описанной композиции плоскостью, проходящей через центры трех сфер. Искомое расстояние будет длиной отрезка $OD$ на этой плоскости.

$PIC$

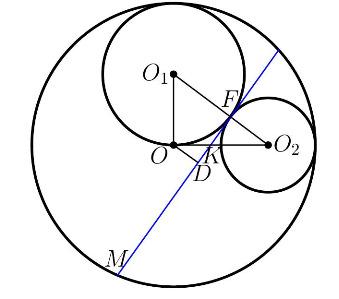
Пусть радиусы малых окружностей равны $2r$ и $3r.$ Тогда радиус наибольшей (внешней) равен $6r$ (дано: $6r= R$ ). Рассмотрим $△O1OO2.$ Его стороны равны $3r,4r$ и $5r,$ следовательно, он прямоугольный.

Обозначим точку пересечения искомой хорды с отрезком $O1O2$ через $F,$ а с отрезком $OO2$ через $K.$ Опустим из центра наибольшей окружности перпендикуляр $OD$ на искомую хорду (отрезок общей касательной). Тогда искомая хорда делится точкой $D$ пополам и перпендикулярна отрезкам $OD$ и $O1O2.$

Прямоугольные треугольники $O1OO2,KFO2,KDO$ подобны. Поэтому $KO O O F-O2= -O1O-2 2 2$ , откуда $5 KO2 = 2r$ и $3 KO = 2r.$

Далее, $OD- OO2-- KO = O1O2,$ откуда $6 1 OD = 5r= 5R.$

Ответ: 0,2 R

Ошибка.
Попробуйте повторить позже

Задача 8#71016

В уравнении

2022 2021 2020 x − 2x − 3x − ...− 2022x− 2023 =0

можно как угодно переставлять коэффициенты при всех степенях $x$ , кроме самой старшей. Можно ли такой перестановкой добиться, чтобы уравнение имело хотя бы два положительных корня?

Источники: Надежда энергетики-2023, 11.3 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Давайте подумаем, какой в этой задаче может быть ответ: если ответ да, то необходимо предъявить пример. Не очень хочется подбирать коэффициенты и искать корни. Давайте попробуем доказать, что, как бы мы не меняли коэффициенты местами, положительных корней будет не больше 1. На что вас наводит последнее предложение?

Подсказка 2

На монотонность! Вспомните, если функция строго монотонна, то она имеет не более 1 корня. Давайте попробуем найти здесь что-то похожее. Пускай (a₂, a₃, ..., a₂₀₂₃)- произвольная перестановка чисел (2, 3, ..., 2023). Тогда наш многочлен имеет вид: x²⁰²²-a₂x²⁰²¹-...-a₂₀₂₃=0. Нам мешаются минусы, может, перенести их в правую часть?

Подсказка 3

x²⁰²²=a₂x²⁰²¹+...+a₂₀₂₃. Теперь справа у нас монотонная функция, при x>0. Но слева у нас также монотонная функция, поэтому сразу завершить решение не получится. Что можно сделать, чтобы слева у нас стояла константа?

Подсказка 4

Можно поделить обе части на x²⁰²² (т.к. нас интересуют положительные корни, мы можем это сделать). Тогда: 1=a₂/x+a₃/x²+...+a₂₀₂₃/x²⁰²². Что мы можем сказать про функцию, стоящую справа?

Подсказка 5

Она строго убывает. Действительно, при увеличении x знаменатель каждой дроби увеличится, а значит, сами они уменьшатся. ⇒ Справа функция монотонно убывает, а слева константа, равная 1 ⇒ она пересекает ее не более чем в 1 точке. Победа!

Показать ответ и решение

Докажем, что это невозможно.

От исходного уравнения перейдем к уравнению, в котором коэффициенты многочлена образуют произвольную перестановку $(a2,a3,...,a2023)$ из чисел ${2,3,...,2023}:$

2022 2021 2020 x − a2x − a3x − ...− a2022x− a2023 = 0

Заметим, что $x= 0$ не является корнем уравнения, т.к. при его подстановке в уравнение получим:

− a2023 =0,

что неверно.

Перенесём все отрицательные члены направо, а затем поделим уравнение на $x2022$ (при условии $x⁄= 0$ ):

x2022 = a2x2021+a3x2020+ ...+ a2022x +a2023

1= a2+ a32 + ...+ a22020221 + a22002322 x x x x

В правой части уравнения получили строго монотонно убывающую на положительной полуоси функцию:

f(x)= 20∑22ak+1 k=1 xk

Доказательство строгой монотонности: пусть $x1 > 0,x2 > 0,x1 <x2.$ Тогда для любого $k ∈{1,2,...,2022}$ выполнено:

ak+k1< ak+k1⇒ f(x2)< f(x1) x2 x1

Строгое монотонное убывание $f(x)$ на положительной полуоси означает, что она пересекает горизонтальную прямую $y = 1$ в единственной точке, которая и будет единственным положительным корнем исходного уравнения.

Ответ: нет

Ошибка.
Попробуйте повторить позже

Задача 9#71015

Найдите максимальное значение величины $x2+ y2 +z2,$ если известно, что

2 2 2 x +y + z = 3x+8y+ z.

Источники: Надежда энергетики-2023, 11.2 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

На что намекает сумма квадратов?)

Подсказка 2

На квадрат длины вектора! Введем декартову систему координат. С левой части мы разобрались - это квадрат длины вектора (x, y, z). А чем является правая часть?)

Подсказка 3

Правая часть - это скалярное произведение векторов a = (x, y, z) и c = (3, 8, 1). Теперь правую часть можно оценить сверху с помощью длин сомножителей, осталось лишь сделать вывод) Помним, что вектор c - фиксированный!

Показать ответ и решение

Введем декартову систему координат и рассмотрим произвольный вектор $a$ с координатами $(x,y,z)$ и фиксированный вектор $c$ с координатами $(3,8,1)$ . Тогда левая часть условия представляет собой квадрат длины вектора $a,$ а правая — скалярное произведение векторов $a$ и $c :$

2 |a|= (a,c)

Оценивая скалярное произведение через длины сомножителей, получаем

2 |a| ≤|a|⋅|c|⇔ |a|≤ |c|

Как известно, равенство возможно, а достигается при векторах, лежащих на одной прямой. Поэтому максимальное значение будет достигаться, например, при $a = c.$

Подставляя значения, получаем $32+ 82 +11 = 74.$

Ответ: 74

Ошибка.
Попробуйте повторить позже

Задача 10#71014

Каждый из шести домов, стоящих на одной стороне улицы, соединен кабельными воздушными линиями с каждым из восьми домов на противоположной стороне. Сколько попарных пересечений образуют тени этих кабелей на поверхности улицы, если никакие три из них не пересекаются в одной точке? Считайте, что свет, порождающий эти тени, падает вертикально вниз.

Источники: Надежда энергетики-2023, 11.1 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Нас просят найти количество попарных пересечений! Для начала давайте разберемся, а когда образуется одно попарное пересечение?

Подсказка 2

Да, пересечение образуется, когда мы выбираем два дома на одной стороне(различных), два дома на другой стороне(тоже различных) и делаем биекцию между ними(то есть, соединяем один дом ровно с одним другим). Остаётся посчитать количество таких четверок домов!

Подсказка 3

Первые два дома нужно выбрать из 6, а вторые два из 8. То есть, это просто число сочетаний из 6 по 2 и число сочетаний из 8 по 2!

Показать ответ и решение

Возьмем произвольную пару домов на одной стороне улицы и произвольную пару на другой. Они являются вершинами выпуклого четырехугольника (поскольку две стороны четырехугольника, идущие от каждой выбранной пары, лежат по одну сторону прямой, т.е. углы не превосходят $∘ 180$ ), следовательно, его диагонали пересекаются.

Каждое попарное пресечение теней (кабелей) является точкой пересечения диагоналей такого четырехугольника. Таким образом, осталось найти их количество, которое равно произведению способов выбрать пару домов на каждой стороне улицы.

C26 ⋅C28 = 420

Ответ: 420

Ошибка.
Попробуйте повторить позже

Задача 11#76464

Охотник Пулька для своей собаки Бульки заказал на АлиЭкспресс три куля собачьего корма. Наутро после доставки один куль оказался съеден. Под подозрение попали четверо, и Незнайке удалось установить следующее.

(1) Если алиби Пончика истинно, то Сиропчик также имеет алиби.

(2) Если Пончик ел корм, то либо Сиропчик, либо Авоська тоже ел корм (либо оба вместе).

(3) Из двух показаний: «Авоська ел корм», «Пончик не ел, но при этом ел Небоська» - хотя бы одно истинное.

(4) Если Небоська ел корм, то также ел либо Авоська, либо Сиропчик (либо оба вместе).

Кого из подозреваемых Незнайка может гарантированно обвинить в поедании за ночь целого куля собачьего корма?

Источники: Надежда энергетики-2022, 11.5 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Начнём с рассмотрения третьего пункта. Условие на авоську мы никак не можем связать с другими фактами, так что давайте предположим, что Небоська ел, а Пончик нет. Тогда надо найти следствия этих фактов из других пунктов и сопоставить их друг с другом. Что мы можем сказать теперь?

Подсказка 2

Да, из 4 мы знаем, что вместе с Небоськой также ели Авоська и Сиропчик, но из 1 нам известно, что если Пончик не ел, то и Сиропчик тоже. Тогда получается, что первое условие из 3 в любом случае выполняется

Показать ответ и решение

Начнем с (3). Пусть Авоська не ел корм. Тогда Пончик не ел, а Небоська ел. Из (4) получаем, что либо Авоська ел, либо Сиропчик. При сделанном предположении это означает, что ел Сиропчик. Но из (1) следует, что Сиропчик не ел корм, т.к. Пончик не ел. Получено противоречие. Следовательно, Авоська виновен (корм ел).

Рассмотреть все варианты для трех оставшихся подозреваемых,


	Авоська	Небоська	Пончик	Сиропчик

1	ел	ел	ел	ел

2	ел	ел	ел	нет

3	ел	ел	нет	ел	невозможно в силу (1)

4	ел	ел	нет	нет

5	ел	нет	ел	ел

6	ел	нет	ел	нет

7	ел	нет	нет	ел	невозможно в силу (1)

8	ел	нет	нет	нет

Видно, что каждый из подозреваемых мог как есть, так и не есть корм.

Ответ: Авоська

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#76463

На каждой из сторон параллелограмма выбрано по произвольной точке. Точки на соседних сторонах параллелограмма соединены отрезками прямых. В результате от параллелограмма оказываются отсеченными четыре треугольника. Вокруг каждого из этих треугольников описана окружность. Докажите, что центры этих окружностей являются вершинами некоторого параллелограмма.

Источники: Надежда энергетики-2022, 11.4 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Взглянув на условие, кажется, что надо доказать что-то страшное и непонятно, как это делать. Но давайте вспомним, какие в принципе у нас есть способы решения задач по планиметрии? Углы считать мы не пойдём, в лоб доказывать равенство сторон тоже. Как можно сделать это хитрее?

Показать доказательство

Изобразим окружности и их центры, которые обозначим $O ,...,O . 1 4$ Рассмотрим векторы $O O ,O O 1 2 4 3$ и $O O ,O O . 1 4 2 3$

$PIC$

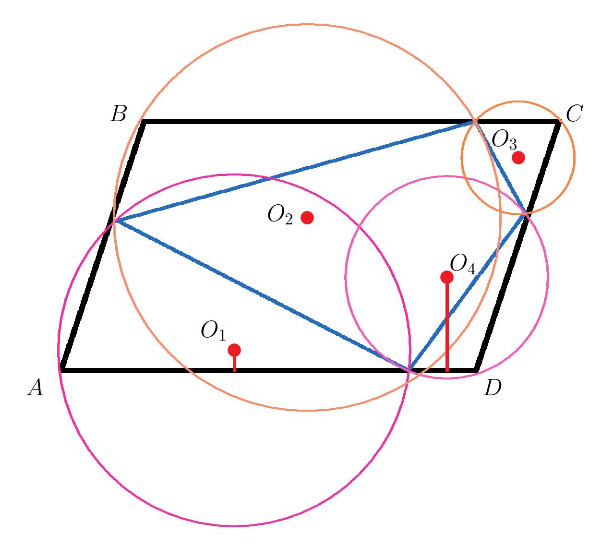
Поскольку центры описанных окружностей лежат на пересечении серединных перпендикуляров, проекции указанных векторов на стороны исходного параллелограмма будут равны половине этих сторон.

Таким образом, если ввести две оси: одну параллельно стороне $AB,$ а другую параллельно стороне $AD,$ то каждая пара рассматриваемых векторов будет иметь одинаковые проекции на каждую из введенных осей. Отсюда следует попарное равенство самих векторов.

Ошибка.
Попробуйте повторить позже

Задача 13#76462

Колхоз имени Лопе де Вега планирует построить на своих землях два одинаковых прямоугольных в плане розария и квадратный в плане свинарник. Сумма периметров розариев должна быть больше периметра свинарника на 16 м, а суммарная площадь розариев превышать площадь свинарника на 16 кв. м. Если такой план может быть реализован, то найдите длины сторон всех строений. Если план нереален, то объясните почему.

Источники: Надежда энергетики-2022, 11.3 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Давайте для начала попробуем записать условие в виде системы уравнений. Какие для этого следует ввести переменные? Что связывает значения периметра и площади?

Подсказка 2

Конечно, обозначим через х и у стороны прямоугольников и через а сторону квадрата. Теперь можем составить уравнения из условий про периметры и площади. Выразим х из уравнения х+у-а=4 и подставим во второе, мы получили квадратное уравнение относительно у. Вспомните, что в условии сказано либо найти все переменные, либо доказать, что таких не бывает. Как можно проверить существование решений?

Подсказка 3

Конечно, дискриминант должен быть неотрицательным. Остаётся только найти подходящие значения а и решить систему для таких значений

Показать ответ и решение

Обозначим стороны прямоугольников через $x$ и $y,$ сторону квадрата через $a$ и составим систему уравнений

{ 2(2x+ 2y)− 4a= 16 { x+ y− a= 4 2xy − a2 = 16 ⇔ 2xy− a2 = 16

Выразим из первого уравнения $x =4 +a− y$ и подставим во второе

2(4+a − y)y− a2 =16

−2y2+2(a+ 4)y− a2− 16

Это квадратное относительно $y$ уравнение. Оно имеет решение, если его дискриминант неотрицателен. Дискриминант (без учета множителя 2) равен

(a+ 4)2 − 2a2− 32 =a2+ 8a+ 16 − 2a2− 32=− (a − 4)2

Отсюда сразу получаем, что $a =4$ и для поиска сторон прямоугольника систему

{ x+ y = 8 2xy =32

имеющую единственное решение $x =y =4.$

Ответ:

Все помещения — квадраты со стороной 4 ед. длины.

Ошибка.
Попробуйте повторить позже

Задача 14#76461

Найдите все целочисленные решения данного уравнения, если таковые существуют.

[-x-] [x+-1] [x+-2021] lg(2x-+1)−-lg6 2022 + 2022 + ⋅⋅⋅+ 2022 = lg5− lg10

Через $[a]$ здесь обозначена целая часть числа $a.$

Источники: Надежда энергетики-2022, 11.2 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Первое, что нужно понять - не стоит бояться задач, которые выглядят громоздко. Они милые внутри. К примеру, в этой задаче, можно взять разные d, разные x, и найти чему будет равна сумма слева, а потом доказать, что так будет всегда. Не могли же нам дать какой-то гроб, где и слева страшная бяка и справа логарифмы, которые вообще мало связаны с нашим «целым» миром.

Подсказка 2

Первое, что надо сделать, чтобы найти эту сумму, это сказать, что x = kd + m. Иначе, не понятно, как можно искать эти самые целые частные от деления на d. Теперь нам надо понять, с какого момента каждая скобка становится равна не k, а k + 1. И посмотреть по сколько у нас значений k и k + 1.

Подсказка 3

Верно, значений k у нас d - m штук, а значений k + 1 ровно m. Значит наша сумма - это k(d - m) + m(k + 1) = kd + m = x. Ого, а теперь задача не такая уж и страшная! Остается преобразовать левую часть по формуле разность логарифмов и получить уравнение вида log_2((2^x + 1)/6) = -x. А это уже крайне понятно решается(квадратно уравнение на 2^x).

Показать ответ и решение

Докажем, что если $x$ целое, $d$ натуральное, то

[x] [x-+1] [x+-d−-1] d + d + ⋅⋅⋅+ d = x

Представим $x$ в виде $x= kd+m,$ где $k∈ ℤ$ (неполное частное), $m ∈ {0,1,...,d − 1}$ (остаток). Тогда величины

[ ] [ ] [ ] x , x+-1 ,..., x+-(d−-m-− 1) d d d

будут равны $k.$ Их количество равно $d− m.$

Величины

[ ] [ ] x-+(d−-m) ,..., x+-(d-− 1) d d

будут равны $k +1.$ Их количество равно $m.$

Итого получаем

[ x ] [x +1] [x+ 2021] 2022 + -2022 +⋅⋅⋅+ --2022-- =k ⋅(d− m)+ (k+1)⋅m = kd+m = x

Преобразуем правую часть уравнения

x x lg(2-+1)−-lg6-= lg[(2-+1)∕6]=− log2[(2x+ 1)∕6] lg5− lg 10 lg1∕2

Таким образом, приходим к уравнению

log [(2x+1)∕6]=− x 2

2x+1 =6 ⋅2−x

Обозначая $t= 2x$ и решая полученное квадратное уравнение, находим, что $2x = 2$ (другой корень не подходит по знаку).

Следовательно, единственное решение $x= 1.$

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 15#76460

Энергетические затраты Пончика во время еды пропорциональны корню квадратному из объема съедаемой порции. Что выгоднее для экономии энергетического запаса: съесть свежую кулебяку как одну порцию или разделить ее на две? В какое максимальное количество раз (и в какую сторону) изменятся затраты при разделении кулебяки на две порции?

Источники: Надежда энергетики-2022, 11.1 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Понятно, что нужно как-то ввести переменные. Пусть две порции относятся друг к другу по величине как с. Также нам нужен какой-то коэффициент пропорциональности, который можно обозначить за а. После этого остается записать отношение двух величин — когда мы едим одну порцию и когда две — через с и х. (где х — переменная: размер, например, первой порции).

Подсказка 2

Мы хотим исследовать это выражение относительно с и найти его экстремум. Он может быть найден с помощью производной или из других соображений.

Показать ответ и решение

Пусть кулебяка делится на порции объёмом $x$ и $cx(c> 0).$ Тогда при съедании всей кулебяки энергетические затраты составят $√ ----- S1 = α x+cx,$ а при разделении на две порции составят $√- √-- S2 =α x+ α cx.$ Требуется исследовать отношение этих величин. Для удобства рассмотрим квадрат их отношения

( S2)2 α2(√x + √cx)2 (1+ √c)2 1+ c+ 2√c- 2 S1 = -α2√x-+cx2--= -1-+c--= ---1+c---= 1+ 1∕√c+-√c

Величина $1∕√c+ √c≥ 2,$ поэтому

(S2)2 =1 +--√-2-√- ≤2 S1 1∕ c+ c

Таким образом, $S2 √- 1< S1 ≤ 2.$

Ответ:

Выгоднее съесть как одну порцию

В $√ - 2$ раз

Ошибка.
Попробуйте повторить позже

Задача 16#88170

Две равные окружности пересекаются в точках $P$ и $Q$ . Произвольная прямая, проходящая через $Q$ , повторно пересекает окружности в точках $A$ и $B$ , а касательные к окружности в этих точках пересекаются в точке $C$ . Докажите, что отрезки $AQ$ и $CB$ видны из точки $P$ под одинаковыми углами.

Подсказки к задаче

Подсказка 1

Доказать, что отрезки видны под равными углами из точки Р равносильно равенству углов APQ и CPB. Чему можно приравнять углы APQ и QPB?

Подсказка 2

Углы APQ и QAC равны, поэтому осталось показать равенство углов САВ и СРВ. О чём говорит равенство САВ и СРВ?

Подсказка 3

Да, оно равносильно вписанности четырёхугольника CAPB. Чтобы доказать это, воспользуемся признаком вписанности, использующим сумму двух противоположных углов!

Показать доказательство

$PIC$

По теореме об угле между касательной и хордой $∠BAC =∠QP A,$ $∠CBA =∠BP Q.$ Следовательно,

∠BP A +∠ACB =∠BAC +∠ACB + ∠CBA = π,

т.е. четырехугольник $APBC$ вписанный. Значит,

∠BP C = ∠BAC = ∠QP A

Другие случаи расположения точек рассматриваются аналогично, например, на втором рисунке

∠ACB =∠CAQ − ∠CBQ =(π− ∠QP A)− (π− ∠QP B)= ∠APB

и

∠QP A= ∠BAC = ∠BP C

$PIC$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#79621

Для каждого целого значения параметра $K$ решите систему уравнений

{ 2[x]+ y = 3∕2; ([x]− x)2− 2[y]= K.

Здесь $[x]$ означает целую часть числа $x$ .

Источники: Надежда энергетики-2020, 11.2 (см. energy-hope.ru)

Подсказки к задаче

Подсказка 1

Когда видим операцию взятия целой части, то стандартной идеей является разложение в виде суммы целой и дробной части.

Подсказка 2

Пусть x = m + a, y = n + b, где m и n — это целые числа, a и b – числа из промежутка [0; 1) Подставим наши разложения в первое уравнение, что тогда можно сказать про b?

Подсказка 3

2m+n+b=3/2, значит, b = 1/2, n = 1 – 2m. Подставим полученные значения во второе уравнение.

Подсказка 4

Учитывая, что K – целое число, чему тогда равно a? Как K можно выразить через m?

Показать ответ и решение

Пусть

x =m + a, y = n+ b, m, n ∈ℤ, a, b∈[0;1)

Из первого уравнения получаем

3 2m + n+ b= 2 ⇒ b= 0,5 n =1− 2m

Подставим эти значения во второе уравнение:

2 (−a )− 2(1− 2m )=K

Тогда

3 a= 0, K = 4m − 2, x= m, y = 2 − 2m

Ответ:

Если $K = 4m − 2,$ где $m ∈ℤ,$ то $x= m, y = 3− 2m. 2$

При других $K$ решений нет.

Ошибка.
Попробуйте повторить позже

Задача 18#76735

Решите уравнение с тремя неизвестными

Y Z X + Y = XY Z

в натуральных числах.

Подсказки к задаче

Подсказка 1

Понятно, что таковое равенство может редко когда достигаться, так как слева что-то почти всегда большее чем справа(степень растет быстрее произведения). Значит, нужно сделать какую-то понятную оценку, а все случаи, которые под нее не подходят, перебрать. Мы хотим какими-то неравенствами получить XYZ, как оценку снизу. Что мы знаем из неравенств? Как это неравенство нам поможет в оценке XYZ(желательно несколько симметрично относительно X и Z, так как очень похожее структурно)?

Подсказка 2

Да, хочется применить неравенство о средних для двух чисел, но как? Нам нужно как-то X^Y перейти к произведению XY*(что-то, не обязательно константное). Аналогично, со вторым слагаемым. Если X >= 2, то X^k >= 2^k, k - натуральное. При этом, 2^k >= 2k(доказывается по индукции), или 2^(k - 1) >= k. Как с этим знанием найти эту оценку?

Подсказка 3

Верно, можно сделать оценку, что X^Y >= X^2 * X^(Y - 2) >= X^2 * 2^(Y - 2) >= X^2*Y/2. При этом, если бы X >= 3, то мы могли бы сказать, что X^(Y - 1) >= 3^(Y - 1) > 2 ^ (Y - 1) > Z^2/2(при Z > 4, остальные Z перебираются). Значит, можно это неравенство применить на второе слагаемое в левой части уравнения.

Подсказка 4

Тогда, Y^Z = Y^(Z - 1) * Y >= 3^(Z - 1) * Y >= Z^2*Y/2. Почему это хорошие оценки? Потому что у нас получается идеальные слагаемые для оценки их как неравенства о средних(Z^2*Y/2 и X^2*Y/2), так как степень каждой переменной будет равна 2/2 = 1, а коэффициент будет равен 1(из за 1/2 перед каждым слагаемым). Значит, при Х >= 2, Y >= 3 у нас есть строгая оценка, что левая часть больше правой. Отсюда, осталось грамотно перебрать меньшие, но это уже задача вполне рабочая.

Показать ответ и решение

1) Рассмотрим случаи. При $Y = 1$ получаем уравнение:

X +1 =XZ

откуда $X (Z − 1)= 1$ , то есть $X =1$ , $Z = 2$ .

2) При $Y = 2$ получаем уравнение:

2 Z 2 Z 2 X + 2 = 2XZ ⇐⇒ (X − Z) +2 − Z =0

При $Z =1$ решений нет. При подстановке $Z = 2,3,4$ получаем решения $(2;2;2)$ , $(2;2;3)$ , $(4;2;3)$ , $(4;2;4)$ . При $Z > 4$ будет выполнено, что $2Z >Z2$ и тогда решений не будет.