Ошибка.
Попробуйте повторить позже
Вписанная окружность треугольника с центром в точке
касается сторон
соответственно в точках
. Точки
и
симметричны вершине
относительно прямых
и
соответственно. Окружности,
построенные на отрезках
и
как на диаметрах, вторично пересекаются в точке
. Докажите, что
лежит на прямой
.
Источники:
Подсказка 1
Хочется с самого начала понять, что за точка K нам дана. Заметим, что одна сторона у наших треугольников одинаковая на будущее. К тому же из условия вытекает, что какие-то углы прямые. Тогда чем же является точка K на нашей картинке?
Подсказка 2
Верно, точка K лежит на отрезке FE и является серединой, так как FIE равнобедренный. Теперь когда объекты на картинке так или иначе связаны, то можно вернуться к вопросу задачи. Что если посмотреть на четырёхугольник NFME. Чем в нём является K? Если же K будет лежать на NM, то что должно выполняться?
Подсказка 3
Верно, K середина диагонали и, если NFME будет параллелограммом, то K как раз будет лежать на NM. Осталось доказать это. Причём мы знаем, что NF =AF = AE = EM, как отрезки касательных из одной точки и симметрии. Остаётся только ввести стандартно углы треугольника, посчитать немного, и победа!
Проведем . Так как окружности построены на диаметрах,
Следовательно, точка — середина отрезка
, так как
и
— высота равнобедренного треугольника
Проведем и
.
как отрезки касательных, и в силу симметрии получаем
Обозначим углы
![]()
Тогда . И
. Следовательно,
, и тогда
Аналогичным счетом углов показываем, что и
Следовательно, — параллелограмм. В нем
— середина диагонали
. Диагонали параллелограмма точкой пересечения
делятся пополам, поэтому
— середина
Ошибка.
Попробуйте повторить позже
Фигура оборотень бьёт все клетки, находящиеся от неё через клетку слева, справа, сверху или снизу, а также бьёт клетку, на которой стоит.
Какое наименьшее количество оборотней необходимо поставить на клетчатую доску , чтобы эти фигуры били все клетки
доски?
Источники:
Подсказка 1
Оборотни на каких множествах клеток точно друг друга не бьют? Попробуем найти такие участки (множества клеток), на которых мы сможем оценить количество оборотней.
Подсказка 2
Оборотни, стоящие на квадрате 2*2, друг друга точно не бьют. Как, исходя из этого соображения, найти 4 множества клеток, которые замещают всю доску и в которых мы сможем оценить количество оборотней?
Подсказка 3
Рассмотрите множества клеток, получаемые всевозможными путями оборотня из каждой клетки углового квадрата 2*2. В каждом таком множестве по 16 клеток. Осталось лишь оценить количество оборотней в каждом таком множестве!
Раскрасим клетки доски в цвета следующим образом: все клетки, куда может прийти оборотень из, не умаляя общности, левой нижней
угловой клетки, покрасим в первый цвет. Сдвигами этого множества клеток вправо, вверх и вправо вверх получаем
множества
клеток.
![]()
Рассмотрим одно из них. Чтобы все клетки были побиты, нужно как минимум оборотня, так как каждый из них бьет не более
клеток, и, следовательно,
и меньше оборотней бьют максимум
клеток. Пример расстановки
оборотней: выделим
непересекающихся Т-образных фигур, в каждой из которых отметим по одному оборотню.
И так как оборотень, стоящий на клетке из одного множества, не может дойти до клеток из трех других, получаем, что всего нужно как
минимум оборотней.
Ошибка.
Попробуйте повторить позже
Натуральные числа от 1 до 8 расставили по кругу так, что каждое число делится на разность своих соседей. Известно, что числа 2 и 5 стоят рядом. Докажите, что числа 4 и 6 стоят рядом.
Источники:
Подсказка 1
Будем отталкиваться от того, что нам уже дано. Какие числа можно поставить рядом с 2? Какие - рядом с 5?
Подсказка 2
Рядом с 2 может стоять одно из чисел 3, 4 ,6, 7. Рядом с пятеркой - 1, 3, 7. Переберем случаи! От какого еще числа удобно отталкиваться?
Подсказка 3
Помним, что соседями единицы могут быть только последовательные числа.
Рядом с может стоять одно из чисел
. Рядом с пятеркой —
. Заметим также, что соседями единицы могут быть только два
последовательных числа. Переберем всевозможные варианты для соседа двойки:
1) Рядом с 2 стоит 3. Тогда рядом с 3 может стоять только 1. Ее сосед — это только 4 и рядом с 4 может встать только 6.
2) Рядом с 2 стоит 4. Тогда рядом с 4 может стоять или
.
Ошибка.
Попробуйте повторить позже
Положительные числа таковы, что
Докажите, что
Источники:
Подсказка 1
Рассмотрим подкоренные выражения. Что можно сказать о них? Как использовать условие?
Подсказка 2
Раскрыв скобки под корнями и применив условие, получаем возможность избавиться от корней! Переходим к новому неравенству - очень уж оно напоминает условие;)
Подсказка 3
Получаем, что a^2 + b^2 + c^2 + 3 abc >= 2*sqrt(abc). Как применить условие? Остаётся несложно неравенство, которое очень напоминает кое-что известное!
Рассмотрим одно из подкоренных выражений
По условию , поэтому подкоренное выражение равно
, и, так как
,
.
Для оставшихся слагаемых рассуждения аналогичные
Пользуясь равенством из условия, получаем
Верное для любых неравенство.
Ошибка.
Попробуйте повторить позже
Можно ли в клетках квадрата расставить числа от 1 до 36 (каждое по одному разу) так, чтобы 6 сумм по горизонтали и 6 сумм по
вертикали в некотором порядке являлись 12 последовательными числами?
Источники:
Подсказка 1
Обозначим первую из 12 последовательных сумм за n. Какие числа входят в эти суммы? Что можно сказать о сумме всех сумм по горизонтали? А по вертикали?
Подсказка 2
Заметим, что при подсчёте всех горизонтальных сумм мы каждое число в таблице посчитали один раз. Тогда чему будет равна сумма всех таких 12ти сумм?
Подсказка 3
Удвоенной сумме всех чисел в таблице. Может ли быть такое? Проверим уравнением
Предположим, что можно. Сумма всех чисел равна . А удвоенная их сумма равна
. Посчитав
суммы арифметических прогрессий, получаем
Противоречие, так как
Ошибка.
Попробуйте повторить позже
Петя и Вася играют в следующую игру. Петя в каждую клетку таблицы 8 × 8 записывает число от 1 до 64, используя каждое по одному разу. После этого Вася выбирает одну из клеток и ставит на эту клетку ладью. Затем он выбирает вторую клетку, на которую можно переместиться одним ходом ладьи из первой клетки, и перемещает ладью на эту клетку. Далее он выбирает третью клетку, на которую можно переместиться одним ходом ладьи из второй клетки, и перемещает ладью на эту клетку. Выбирать ранее посещённые клетки запрещено. После этого Вася складывает все три числа, записанных в клетках, на которых стояла ладья. Какую максимальную сумму гарантированно может получить Вася независимо от того, каким способом Петя заполнит таблицу? (Ладья может перемещаться на любое количество клеток по горизонтали или вертикали.)
Источники:
Лемма. а) На доске выбраны 11 произвольных клеток. Тогда среди них можно найти три клетки такие, что от одной их них можно
двумя ходами ладьи обойти вторую и третью клетки.
б) На доске, суммарное числом столбцов и строк в которой не более 11, выбраны 8 клеток. Тогда среди них можно найти три клетки такие, что от одной их них можно двумя ходами ладьи обойти вторую и третью клетки.
Доказательство леммы. Если в столбце/строке выбрана одна клетка, будем называть её одиночной, а если две — будем называть каждую из двух клеток парной. Будем говорить, что клетка занимает строку/столбец, если она стоит в этой строке/столбце. Заметим, что никакие другие клетки не могут быть выбраны в столбце/строке, где стоит одиночная или парная клетки. Тогда каждая пара клеток занимает суммарно 3 строки и столбца, а каждая одиночная — 1 строку и 1 столбец.
a) Обозначим число одиночных клеток за а число парных клеток — за
Если лемма не выполняется, то нельзя 11 клетками занять
более 8 строк и 8 столбцов, то есть 16 в сумме. Тогда имеем систему
Но — противоречие. Следовательно, предположение неверно и пункт а) леммы
доказан.
б) Аналогично пункту а) леммы обозначим число одиночных клеток за а число парных клеток за —
Если лемма не выполняется,
то нельзя 8 клетками занять более 11 строк и столбцов в сумме. Тогда имеем систему
Но — противоречие. Следовательно, предположение неверно и пункт б) леммы
доказан.
Решение
Рассмотрим 11 клеток с числами от 54 до 64. Из пункта а) леммы следует, что какие-то три из них второй игрок может обойти, придерживаясь условий задачи. Минимальная сумма трёх из этих чисел равна
значит второй игрок всегда может получить сумму не менее 165 . Предположим, что сумму больше 165 не всегда
удастся получить. Тогда никакие три из клеток с числами от 54 до 64 помимо 54, 55, 56 не должны оказаться в одной строке/столбце или
образовывать "угол".
| - | - | - | - | - | - | - | - |
| - | - | | - | - | | - | - |
| - | - | - | - | - | - | - | - |
| - | - | - | - | - | - | - | - |
| - | - | - | - | - | - | - | - |
| - | - | - | - | - | | - | - |
| - | - | - | - | - | - | - | - |
| - | - | - | - | - | - | - | - |
При этом числа 54, 55, 56 обязаны оказаться в одной строке/столбце или образовывать "угол иначе найдётся другая тройка чисел с большей суммой. Если эти числа располагаются в одной строке/столбце, или образуют "угол то занимают суммарно 4 строки и столбца. Без ограничения общности, пусть эти числа стоят так, как показано ниже, ведь если поменять какие-то строки/столбцы местами, искомая сумма не изменится.
| 54 | 55 | 56 | X | X | X | X | X |
| X | X | X | - | - | - | - | - |
| X | X | X | - | - | - | - | - |
| X | X | X | - | - | - | - | - |
| X | X | X | - | - | - | - | - |
| X | X | X | - | - | - | - | - |
| X | X | X | - | - | - | - | - |
| X | X | X | - | - | - | - | - |
И в том, и в другом случае оставшиеся 8 клеток с числами от 57 до 64 располагаются в выделенном прямоугольнике, количество строк и
столбцов в которых суммарно равно 12. Если эти 8 клеток занимают не все строки или столбцы, то они занимают суммарно не более 11
строк и столбцов. Тогда из пункта б) леммы следует, что какие-то три числа стоят в одной строке/столбце или образуют “угол”, а значит,
выбрав эти три клетки, мы увеличим искомую сумму. Если эти 8 клеток, среди которых одиночных и
парных клеток, занимают все
строки и столбцы, то имеем систему
откуда Следовательно, все клетки в выделенном прямоугольнике парные. Тогда найдётся число не менее 52 (на второй
таблице число 53 может дополнять серые клетки до квадрата), которое стоит в одной строке или в одном столбце с какой-то парной клеткой
из выделенного прямоугольника. Взяв это число и две парные клетки, получим сумму не менее
Значит, примера,
гарантирующего сумму 165, но не гарантирующего сумму 166, не существует.
Пример, гарантирующий сумму 166, но не гарантирующий сумму 167:
| 64 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 63 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 62 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 61 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 60 | 59 | 46 | 45 | 44 | 43 |
| 31 | 32 | 42 | 41 | 58 | 47 | 50 | 53 |
| 33 | 34 | 40 | 39 | 48 | 57 | 51 | 55 |
| 35 | 36 | 37 | 38 | 49 | 52 | 56 | 54 |
Здесь сумма 166 достигается, например, на числах 54, 55, 57. Все остальные суммы в пределах правого нижнего прямоугольника
не превосходят 166. Максимальная сумма в пределах правого нижнего прямоугольника
не будет превосходить 166, так как
Оставшиеся числа можно ставить в любые из оставшихся клеток, так как максимальная ещё не рассмотренная сумма
будет равна
Ошибка.
Попробуйте повторить позже
Найдите количество троек натуральных чисел , являющихся решением уравнения
Источники:
Подсказка 1
Для каждого значения √(n+√k) значение m будет определено однозначно. Подумайте, какие значения может принимать √(n+√k).
Подсказка 2
√(n+√k) не может быть меньше 2, так как n и k больше 1, и также не может быть больше 2022, так как 2023-m≤2022. Давайте обратим внимание на то, что в правой части уравнения стоит целое число, тогда и в левой части тоже должно быть целое. Какие должны для этого соблюдаться условия?
Подсказка 3
Для этого k и n+√k должны быть точными квадратами. Обозначим k = x² и n+√k = y². В таком случае, число n определяется однозначно, значит, для получения ответа на задачу нам нужно найти все возможные пары (x, y).
Чтобы левая часть была целым числом, числа и
должны быть точными квадратами, при этом
значит
и отсюда
Так как
то
может принимать любое значение от
до
— по этому
значению число
определяется однозначно.
Пусть и
где
и
тогда число
определяется однозначно, а именно
Получается, необходимо посчитать число допустимых пар
Всего их
Формула суммы квадратов первых натуральных чисел известна:
Применим эту формулу и получим
Ошибка.
Попробуйте повторить позже
Положительные числа таковы, что числа
в указанном порядке составляют арифметическую прогрессию и
числа
,
,
,
в указанном порядке составляют арифметическую прогрессию. Докажите, что
.
Источники:
Подсказка 1
Воспользуемся характеристическим свойством арифметической прогрессии и получим четыре уравнения от четырех переменных. Попробуйте преобразовать их таким образом, чтобы получить зависимость b + d от c.
Подсказка 2
Приведем к общему знаменателю уравнение 1/(a+b+c)+1/(a+c+d)=2(a+b+d). Получаем, b²+d²+ab+ad=2c²+2ac. Так же мы знаем, что b²+d²=2c². Попробуйте, пользуясь ранее полученными уравнениями, сперва доказать, что b = d, потом, что c = b, а затем и равенство a = b.
Ошибка.
Попробуйте повторить позже
Существует ли многоугольник, не имеющий центра симметрии, который можно разрезать на два выпуклых многоугольника, каждый из которых имеет центр симметрии?
Источники:
Подсказка 1
Придумывать что-то очень сложное не хочется, поэтому думаем, а на какие простые фигуры, имеющие центр симметрии, хочется разбить наш многоугольник?
Подсказка 2
На прямоугольники! Составим фигуру из них)
Пример:
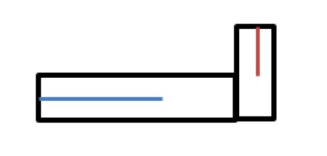
Пример подходит, потому что центрами симметрии прямоугольников являются точки пересечения их диагоналей, а данный многоугольник не имеет центра симметрии, так как если он лежит вне синего отрезка, проходящего через середину одной из сторон, левые вершины многоугольника перейдут не в точки многоугольника, а если он лежит вне красного отрезка, проходящего через середину другой стороны, то верхние вершины многоугольника перейдут не в точки многоугольника.
Ошибка.
Попробуйте повторить позже
Дарья Дмитриевна готовит зачёт по теории чисел. Она пообещала каждому студенту дать столько задач, сколько слагаемых он создаст в числовом примере
где все числа — натуральные, больше 10 и являются палиндромами (не меняются, если их цифры записать в обратном порядке). Если
студент не нашёл ни одного такого примера, он получит на зачёте 2021 задачу. Какое наименьшее количество задач может получить
студент?
Источники:
Подсказка 1
Легко можно придумать пример для трех. Например, 22+888+1111. Попробуйте доказать, что меньше трех придумать невозможно.
Подсказка 2
Пример на одного числа невозможен, так как 2021 - не палиндром. Если же чисел будет два, то одно число обязательно должно быть четырехзначным. Рассмотрите несколько вариантов того, как может выглядеть это четырехзначное число. Подумает, как при этом должно выглядеть второе число в сумме.
Одну задачу студент получить не может, так как 2021 не является палиндромом. Предположим, что он может получить две задачи, тогда
хотя бы одно из чисел — четырёхзначное. Если оно начинается на 2, то вторая цифра 0 и само число равно 2002. В таком случае
второе число равно 19, что не палиндром. Если же число начинается с 1, то его последняя цифра также 1 и у второго числа последняя
цифра должна быть нулём, что неверно для палиндромов. Значит две задачи студент получить не мог. Пример на 3 задачи существует,
например,
Ошибка.
Попробуйте повторить позже
Пусть — множество всех простых чисел, расположенных в некотором порядке. Может ли случиться так, что для всех
натуральных
число
является натуральным?
Источники:
Подсказка 1
В задачах на делимость (а это по сути она и есть) часто выгодно рассмотреть какое-то красивое число. А поскольку у нас в задаче часто фигурируют простые, рассмотрим p_m = 2. Что тогда хорошего можно сказать про дробь?
Подсказка 2
Тогда, можно сказать, что число меньше 2, а значит равно 1, а значит, p_(m + 1) = p^2_(m + 2) + 2. А мы как-то использовали m? Может ли m быть сильно большим? Как можно ограничить m зная симметричность p_(i + 1) и p_i в нашем числе?
Подсказка 3
Если m > 1, то можно взять рассмотреть (2p_(m - 1) - p^2_(m + 1))/(2 + p_(m - 1)). Тогда, p_(m - 1) = p^2_(m + 1) + 2 = (p^2_(m + 2) + 2)^2 + 2. По какому модулю теперь удобно посмотреть, при наличии тут множественных квадратов?
Подсказка 4
Конечно, mod 3. Ведь тогда, если p_(m + 2) != 3, то p_(m + 1) кратен 3, а значит равен 3. Но тогда p_(m + 2) = 1. А если же p_(m + 2) = 3, то p_(m - 1) = 123. Значит, пришли к общему противоречию с тем, что m > 1, значит, m = 1. При этом, поняли, что mod 3 в этой задаче, как будто, играет важную роль. Давайте тогда , если уж все таки хотим делимость, рассмотрим такие p_k и p_k + 1, что их сумма кратна 3, и при этом они оба отличны от 3. Что это значит тогда для этих двух чисел? А для дроби?
Подсказка 5
Это значит, что остатки mod 3 у этих
Подсказка 6
Это числа, которые сравнимы с 2 mod 3, а после идет сама тройка. Но тогда, если после тройки стоит число = 2 mod 3, то после него идут только числа = 2 mod 3, а значит пришли к противоречию, так как числа = 1 mod 3 существуют. А значит, после 3 идут только числа = 1 mod 3, но тогда перед 3 стоит конечное число простых = 2 mod 3. А то, что таких бесконечно - остаётся вам в качестве упражнения! :)))
Предположим, что такое могло случиться. Тогда существует натуральное такое, что
Значит число
является натуральным, откуда
Случай невозможен, так как тогда число
также является натуральным, откуда
Теперь если то
что невозможно. Если же
то
Значит,
Это невозможно. Следовательно,
Предположим теперь, что нашлись числа и
с различными ненулевыми остатками при делении на 3, то есть
Поскольку число
является натуральным, то
Но тогда
Это невозможно, так как квадраты имеют остатки 0 или 1 при делении на 3. В итоге мы доказали, что числа с остатками 1 и 2 при делении на 3 не могут быть соседними.
Поскольку это означает, что после
стоят несколько чисел с остатком 2 при делении на 3, затем где-то стоит
число 3. Если после тройки стоит число с остатком 2 при делении на 3, то все числа далее будут с таким же остатком и в
последовательности простых чисел не будет ни одного числа с остатком 1 при делении на 3 (такие есть, например, число
7).
Следовательно, после тройки стоит число с остатком 1 при делении на 3 и все числа за ним имеют такой же остаток. Но тогда до тройки стоит лишь конечное число простых чисел с остатком 2 при делении на 3.
Предположим, что простых чисел вида конечное число. Обозначим все такие числа через
Число
не
делится на простые числа
и даёт остаток 2 при делении на 3. Значит среди его простых делителей должно быть число вида
— противоречие.
Ошибка.
Попробуйте повторить позже
Назовём число полуцелым, если число
— целое. Полуцелой частью числа
назовём наибольшее полуцелое число, не превосходящее
и будем обозначать
Решите уравнение
Источники:
Подсказка 1
Так, даны какие-то полуцелые части. Понятно, что сразу же напрашивается аналогия с целой и дробной частью. Когда мы делим число x на целую —[x], и дробную — {x} части, мы можем записать, что х=[x]+{x}, где [x] — целое число, а {x} лежит на [0,1). Здесь, чтобы облегчить себе жизнь, поступим так же и запишем подобные ограничения на полуцелую часть числа и “остаток”, который получается после ее вычитания.
Подсказка 2
Если обозначить за n/2 полуцелую часть, то можно записать, что x = n/2+r. Получаем уравнение на n и r и имеем соответствующие ограничения на эти величины. Далее нужно будет активно использовать то, в каких пределах лежит r, и вспомнить, какие приемы можно использовать в подобных задачах с целой и дробной частью.
Подсказка 3
Удобнее будет отдельно рассмотреть положительные и отрицательные n. Дальше только аккуратные преобразования, нахождение n, подстановка и нахождение r :)
Рассмотрим два случая.
1) Число — полуцелое, тогда
и исходное уравнение примет вид
Корнями данного уравнения являются числа но тогда числа
не являются целыми, значит решений
нет.
2) Имеет место равенство
где и
тогда
А также исходное уравнение примет вид
Выразим из уравнения и получим
Решения существуют только при Найдём все
удовлетворяющие неравенству
Если , то
и может иметь решение только лишь неравенство
которое после возведения в квадрат равносильно
Поскольку и
, то
— единственное целое значение, удовлетворяющее
системе. В этом случае
Если то решений нет, так как
— целое.
Если , то
и может иметь решение только лишь неравенство
Поскольку и
то
— единственное целое значение,
удовлетворяющее системе. В этом случае
Ошибка.
Попробуйте повторить позже
Сколькими способами в таблице можно расставить числа от 1 до 9 (каждое по одному разу) так, чтобы в каждом столбце сверху-вниз
и в каждой строке слева-направо числа шли в порядке возрастания?
Источники:
Подсказка 1
Попробуем представить себе расстановку чисел в таблице (от а₁ до а₉). Что можно точно сказать об этих числах?
Подсказка 2
Правильно, в каждом ряду и столбце последующее число больше предыдущего. Подумайте, чему равны первое (а₁) и последнее (а₉) числа, а также попробуйте вывести оценку на а₅.
Подсказка 3
Теперь, имея оценку на а₅, можем разобрать по отдельности все три случая возможного значения.
Подсказка4
Если а₅ = 4 или 6, по очереди находим количество способов расстановки чисел, меньших и больших а₅, а затем перемножаем. Если а₅ = 5, то следует начать с рассмотрения клеток а₃ и а₇ и количества способов для каждого значения цифр, стоящих в этих клетках. Остаётся только проверить, нет ли у нас пересекающихся случаев, и сложить общее количество способов
Пронумеруем клетки таблицы так, как показано на рисунке. Ясно, что в левой верхней клетке стоит число 1, а в правой нижней — число 9.
| 1 | | |
| | | |
| | | 9 |
По условию поэтому
Рассмотрим случаи.
1) Если то числа
и
— это 2 и 3. Способов их расстановки всего 2. Теперь вычислим количество вариантов выбора чисел
и
На их место можно поставить любую из оставшихся пар чисел, причём
поэтому расстановка каждой пары определяется
однозначно. Всего таких пар
Оставшиеся два числа расставляются однозначно. Всего получилось
вариантов
расстановки.
2) Если то числа
и
— это 7 и 8, и случай аналогичен предыдущему. Получаем ещё 12 вариантов расстановки.
3) Если то посмотрим, какие числа могут стоять в клетках с номерами
и
На их место нельзя ставить числа 2 и 8, так
как эти числа обязаны быть соседями 1 и 9 соответственно. Если
то
и
Любое из оставшихся чисел можно
поставить в клетку
тремя способами, оставшиеся числа ставятся однозначно. Рассмотренный вариант аналогичен случаям
и
— в каждом получаем по 3 варианта расстановки, но были дважды посчитаны случаи, когда числа
и
— это
3 и 7. Всего таких случаев два:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 1 | 4 | 7 |
| 2 | 5 | 8 |
| 3 | 6 | 9 |
В итоге получаем вариантов.
Если ни одно из чисел в клетках и
не равно 3 или 7, то в клетках
и
могут стоять лишь числа 4 и 6 в любом порядке.
Тогда в клетках
и
стоят числа 2 и 3 в любом порядке, а в клетках
и
— числа 7 и 8 в любом порядке. Всего 8 вариантов
расстановок.
Все случаи разобраны, искомое число вариантов равно
Ошибка.
Попробуйте повторить позже
В вершинах правильного двенадцатиугольника в некотором порядке расставили натуральные числа от 1 до 12 (каждое по одному разу). Могло ли случиться так, что суммы всех пар соседних чисел являются простыми и суммы всех пар чисел, между которыми стоят ровно два числа, тоже являются простыми?
Источники:
Подсказка 1
Для начала, попробуйте взять любое число от 1 до 12 и посмотреть, сколько чисел в сумме с исходным дают простое число!
Подсказка 2
Да, для каждого числа это индивидуально, поэтому конкретно из этого факта мало что можно извлечь. Но если рассмотреть похожую идею, какие числа в сумме с исходным образуют простое число? И как нам это поможет в задаче?
Подсказка 3
Верно, каждое число влияет ровно на 4 суммы. Так что, если мы найдем два числа, для которых дополнение до простого совпадает, то мы победим! (дополнение – число, которое в сумме с исходным даёт простое)
Подсказка 4
Да, надо посмотреть на числа 6 и 12.
Каждое число в вершине участвует ровно в четырёх суммах. Заметим, что для получения простой суммы к числам 6 и 12 можно прибавить только 1, 5, 7 и 11. Значит для вершин, в которых стоят числа 6 и 12, наборы соседних чисел и чисел, стоящих от них через две вершины, должны совпадать. Однако, для каждой вершины эти наборы различны, поэтому хотя бы одна из сумм не будет являться простым числом.
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике точка
— середина стороны
— точка пересечения медиан,
— центр вписанной
окружности. Известно, что
. Докажите, что
.
Источники:
Подсказка 1
Нужно как-то использовать условие про угол, но углы с серединами сторон обычно очень плохо считаются, нужно как-то использовать, что угол именно прямой...
Подсказка 2
Давайте вспомним, что внутренняя и внешняя биссектрисы одного угла перпендикулярны, это наталкивает нас на мысль рассмотреть...
Подсказка 3
Центр I_a вневписанной окружности! Ведь тогда мы получим, что KI параллельно BI_a.
Подсказка 4
Тогда KI - средняя линия, и мы получаем, что AI=II_a. Мы получили какое-то отношение длин на прямой AI_a. Какой ещё есть факт, связанный с отношениями на этой прямой?
Подсказка 5
Лемма о трезубце! Применив её, мы получим, что IW=WI_a, где W - середина дуги BC. Но это значит, что AI/IW=2/1. Это что-то напоминает... Вспомните, что мы ещё не использовали?
Подсказка 6
Мы ещё ничего не говорили, что точку M пересечения медиан, настало время ей воспользоваться, и тем, что медиана делится в отношении 2/1 точкой M, и задача решится!
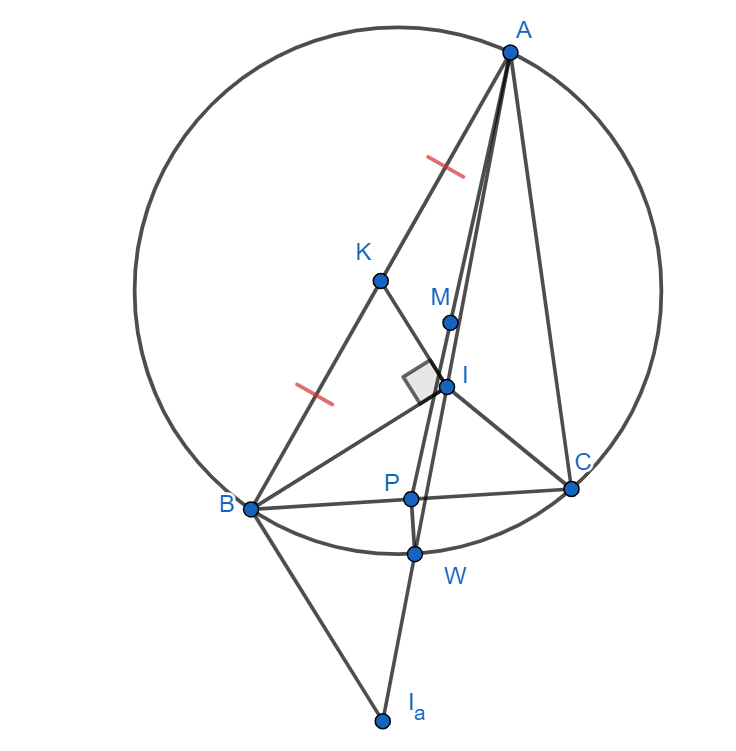
Давайте поймем, как реализовать странное условие про угол. Вспомним про то, что внутренняя и внешняя биссектрисы одно и того же угла
перпендикулярны. Тогда давайте дополнительно отметим центр вневписанной окружности данного треугольника, касающейся стороны
Пусть это
Значит,
Так как то
— средняя линия треугольника
По лемме о трезубце
— середина
следовательно,
Тогда
Пусть — середина стороны
Тогда по свойству медианы:
Тогда
Так как — середина дуги
не содержащей
то
А это означает требуемое.
Ошибка.
Попробуйте повторить позже
На доске размером стоит сказочная шахматная фигура принцесса. За один ход принцесса может передвинуться либо на одну
клетку вправо, либо на одну клетку вверх, либо на одну клетку по диагонали влево-вниз. Какое наибольшее число не бьющих друг друга
принцесс можно поставить на доску?
Заметим, что в прямоугольниках и
находится не больше одной принцессы. Иначе в прямоугольнике
левая принцесса
била бы правую, а в прямоугольнике
нижняя принцесса — верхнюю. Значит, принцессы не могут быть в соседних по стороне
клетках.
Покажем, что в прямоугольнике не более двух принцесс. Предположим, что в таком прямоугольнике можно разместить хотя бы
фигуры принцесс. Так как принцессы не являются соседями по стороне, то возможны два варианта их размещения (розовые квадратики
— фигуры прицесс)
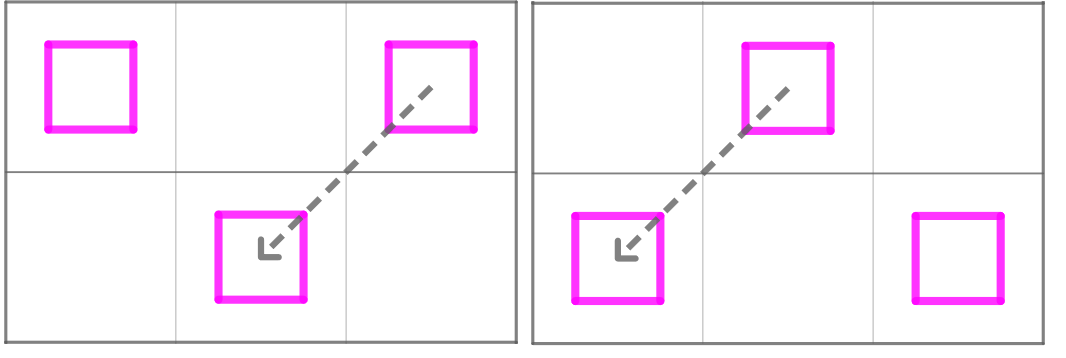
В обоих случаях найдется принцесса, которая будет побита.
Тогда если разбить доску на
непересекающиеся области размера
получим, что принцесс не более
48 принцесс разместить уже возможно:
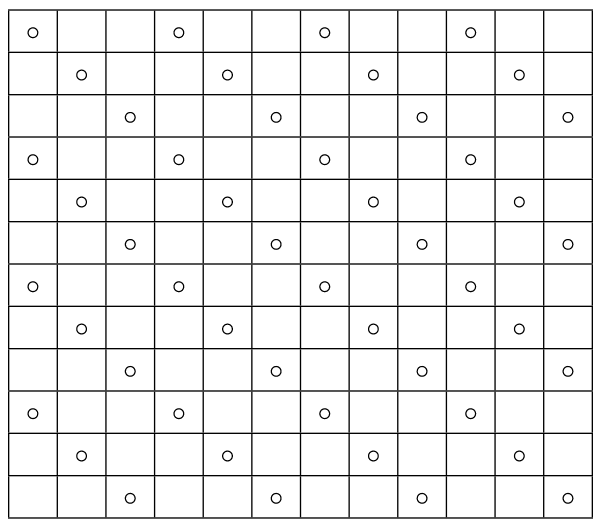
Ошибка.
Попробуйте повторить позже
Максим написал на доске произвольный многочлен с целыми коэффициентами. Антон, не глядя на доску, сказал, что какое бы
натуральное число
не назвал Максим, среди выражений
обязательно найдётся число, кратное
Прав ли Антон?
Заметим, что это следует из того, что
для любого
Рассмотрим сумму
Заметим, что в слагаемые в той сумме разбиваются на
групп так, что в каждой группе
слагаемые имеют вид
(
) и дают одинаковый остаток при делении на
Но тогда сумма слагаемых в
каждой группе кратна
потому что мы суммируем
одинаковых остатков. Но тогда и вся рассмотренная сумма кратна
Да, прав



