Ошибка.
Попробуйте повторить позже
Сфера касается основания
тетраэдра
в точке
и проходит через вершину
. Рёбра
и
эта сфера
пересекает в точках
и
. Центр описанной окружности треугольника
лежит на отрезке
. Радиус сферы
равен
.
Пусть - объём тетраэдра
, а
- объём тетраэдра
. Какое наибольшее значение может принимать
Источники:
Пусть — центр описанной окружности треугольника
, лежащий на
— центр сферы. Очевидно,
— середина
.
Так как точки
и
лежат на сфере,
перпендикулярно плоскости
. С другой стороны,
и
— это одна и
та же прямая, а
перпендикулярна плоскости
. Значит, плоскости
и
параллельны, а тетраэдры
и
подобны.
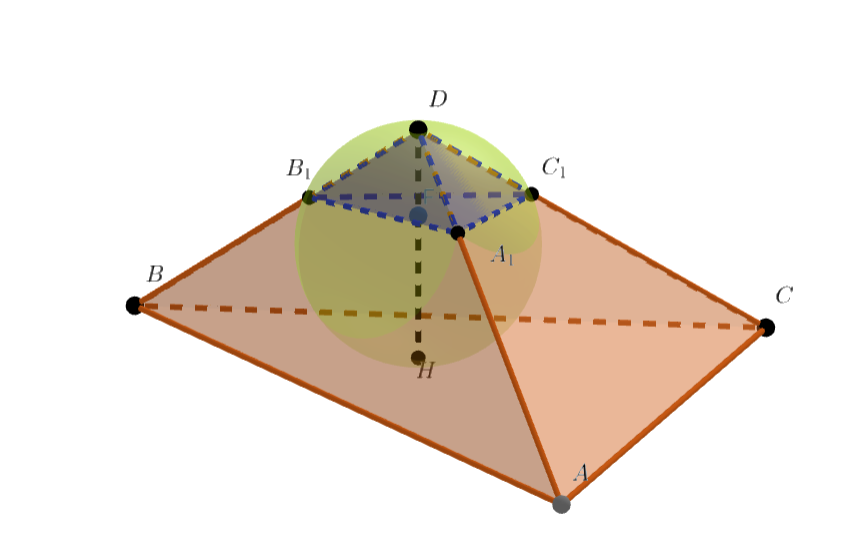
Пусть — длина
, то есть высота маленького тетраэдра. Высота большого тетраэдра равна
, а коэффициент их подобия
.
- прямоугольный треугольник с прямым углом
, значит, радиус описанной окружности
треугольника
, то есть
, равен
Как известно, среди всех треугольников, вписанных в данную окружность, наибольшую площадь имеет равносторонний. Для окружности
радиуса эта площадь составляет
Значит, объемы тетраэдров составляют
и
а их произведение равно
Чтобы максимизировать эту величину, достаточно максимизировать
В первой точке достигается минимум, равный нулю, а во второй — максимум. Подставив в формулу для объёма,
получим
Ошибка.
Попробуйте повторить позже
Дан куб с ребром равным
— сфера, вписанная в каркас этого куба (то есть, касающаяся всех его рёбер). Точка
— середина ребра
Прямая
вторично пересекает сферу
в точке
Найдите
Источники:
Подсказка 1
У нас есть вписанная сфера, а мы хотим найти какой-то отрезок, конец которого лежит на сфере. Может, попробовать применить теорему о касательной и секущей...
Подсказка 2
Наша сфера касается ребра AA₁ в точке K, где K- середина AA₁. Тогда AK²=AX*AM. Надо как-то найти AM...
Подсказка 3
Мы работаем с кубом, поэтому логично было бы поискать теоремки Пифагора. Например для треугольника AMB₁. А почему он прямоугольный?
Подсказка 4
Потому что C₁B₁ перпендикулярен плоскости ABB₁. Тогда по теореме Пифагора для AMB₁: AM²=AB₁²+MB₁². Мы знаем, что B₁M=x/2. Осталось только найти AB₁² и досчитать AX.
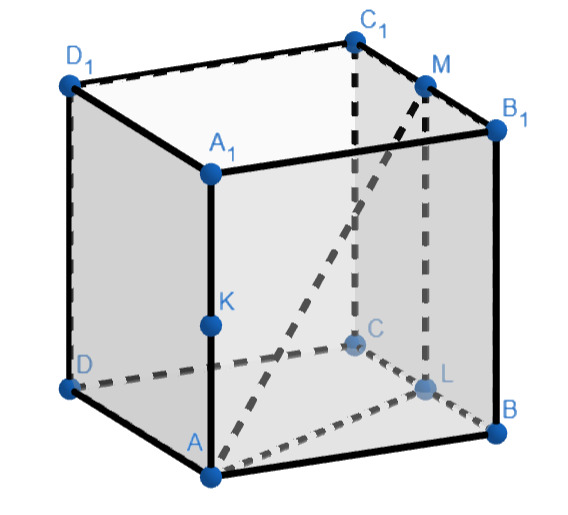
Пусть — середина ребра
тогда
Т.к.
— куб, по теореме Пифагора из прямоугольного
получаем
— середина
а
— середина
следовательно,
как средняя линия квадрата
равна
т.е. равна
Т.к.
— куб, по теореме Пифагора из прямоугольного
получаем
Пусть — середина ребра
тогда
Т.к. сфера
вписана в каркас куба
значит, точками касания
являются середины рёбер. Следовательно, используем теорему о касательной и секущей
Ошибка.
Попробуйте повторить позже
Дана четырёхугольная пирамида в основании которой лежит параллелограмм
Плоскость
пересекает рёбра
и
пирамиды в точках
и
соответственно. Известно, что
Найдите
Источники:
Подсказка 1
У нас уже есть три отношения, но очень хочется заполучить еще и четвертое... Давайте попробуем найти t = OD'/OD. Для этого введем систему координат с центром O и базисными векторами OA, OB и OC. Какие координаты имеют наши точки в этой системе?
Подсказка 2
Очевидно, что A (1, 0. 0), B (0, 1, 0) и C (0, 0, 1). Значит A' (1/a, 0, 0), B' (0, 1/b, 0), C' (0, 0, 1/c). Т.к. ABCD- параллелограмм, то вектор CD = BA = OA-OB. Чему тогда равен вектор OD?
Подсказка 3
Верно, OA-OB+OC! Тогда D (1, -1, 1) ⇒ D' (t, -t, t). Можно заметить, что плоскость α задается в нашей системе координат уравнением ax + by + cz = 1. Поэтому верно равенство at - bt + ct = 1 (Просто подставили точку D' в это уравнение). Итого, t = 1/(a - b + c). А что мы вообще хотели...
Подсказка 4
Нам нужно найти отношение объемов. Мы умеем легко это делать для тетраэдров, поэтому предлагаю разбить нашу пирамиду OA'B'C'D' на два тетраэдра OA'B'C' и OA'C'D'. Тогда V(OA'B'C'D')/V(OABCD) = V(OA'B'C')/V(OABCD) + V(OA'C'D')/V(OABCD). Т.к. ABCD- параллелограмм, то V(OABCD) = 2V(OABC) = 2V(OACD). А чему равно отношения V(OA'B'C')/V(OABC) и V(OA'C'D')/V(OACD)?
Подсказка 5
Т.к. тетраэдры с общим трехгранным углом относятся так же, как произведение отношений соответствующих сторон, то V(OA'B'C')/V(OABC) = 1/abc. Найдите оставшееся отношение и завершите решение!
Отношение объём пирамид с общим трёхгранным углом равно произведению отношений длин рёбер, исходящих из этого угла,
где Поскольку треугольники
и
равны,
Значит,
Дальше можно было бы строить сечение и использовать для подсчёта отношений теоремы Фалеса и Менелая, но мы воспользуемся координатно-векторным методом.
— параллелограмм, поэтому
и, следовательно,
Если точка принадлежит плоскости
а
коэффициенты
и
удовлетворяют уравнению
(это, как известно, уравнение плоскости, даже если система координат не декартова, а точки
и
этому
уравнению, очевидно, удовлетворяют).
Получаем
Обратная величина является ответом к задаче.
Ошибка.
Попробуйте повторить позже
Сфера радиуса 10 вписана в каркас тетраэдра (т.е. касается всех его рёбер). Сумма длин рёбер тетраэдра составляет 180. Докажите, что объём тетраэдра не превосходит 3000.
Подсказка 1
Во-первых, нам надо понять, через что оценивать. Если у нас есть сфера, которая касается ребер, то это значит, что её сечения гранями - это вписанные в треугольники этих граней окружности. А это значит, что мы можем оценивать объем тетраэдра через маленькие тетраэдры OABC, OABD, OACD, OBCD , где О - центр сферы.
Подсказка 2
Понятно, что ситуация относительно каждого тетраэдра равноправна, потому, нам надо получить оценку только на 1 (то есть, если мы получили какую-то оценку на один маленький тетраэдр, то сможем получить эту же оценку и на другие). Возьмем тогда тетраэдр OABC. Если центр вписанной окружности - это I, то объём OABC равен 1/3 * OI * S(ABC). Как нам тогда связать периметр и объем?
Подсказка 3
Верно, нам надо выразить площадь треугольника как p_abc*r (p_abc - полупериметр). Тогда у нас в силу равнозначности тетраэдров и равнозначности сторон треугольника здесь, при суммировании объемов будет один и тот же коэффициент при каждом ребре тетраэдра и значит, мы выразим площадь. Остается связать r*OI(то, что вылезает при подсчете объема) и R(R - радиус сферы). Как связаны эти три отрезка?
Подсказка 4
Они образуют прямоугольный треугольник. При этом, OI^2 + r^2 = R^2. Значит, у нас есть у нас есть факт, что сумма квадратов OI и r равна квадрату R, а мы хотим оценить произведение. Что нам это должно напомнит?
Подсказка 5
Конечно, неравенство о среднем квадратичном и геометрическом. Тогда, произведение OI*r оценивается сверху как R^2/2. Осталось только сложить все неравенства(ведь мы это проделали только относительно одной грани) и получить требуемое.
Обозначим тетраэдр центр сферы, вписанной в каркас —
а саму сферу —
Объём тетраэдра равен сумме объёмов маленьких
тетраэдров
и

Пересечение и плоскости
это вписанная окружность треугольника
Обозначим за
её центр, тогда
— высота
тетраэдра
Пусть
— радиус сферы
— радиус вписанной окружности треугольника
Тогда выполняется равенство
Тогда
![]()
где — полупериметр треугольника
По неравенству о среднем геометрическом и среднем квадратичном
получаем
то есть
Таким образом,
Складывая объёмы четырёх маленьких тетраэдров, получаем
а сумма полупериметров граней это в точности сумма длин рёбер тетраэдра. Значит,



