Последовательности, функции и их кодирование на Верченко —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Последовательности, функции и их кодирование на Верченко

Тема Межрегиональная им. И. Я. Верченко (криптография)

Последовательности, функции и их кодирование на Верченко

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела межрегиональная им. и. я. верченко (криптография)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#71011

Дана последовательность $a,b ,a ,b,...,a,b 1 1 2 2 k k$ , состоящая из $0$ и $1.$ Пусть $N$ — количество чисел $i$ от $1$ до $k$ таких, что $a = 0 i$ и $bi = 1.$ Докажите, что число последовательностей указанного вида, для которых $N$ нечетно, находится по формуле $2k−1 k−1 2 − 2 .$

Источники: Верченко-2022 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

В задаче есть параметр k, учитывая который строятся последовательности. Увеличив k, несложно построить новую последовательность, не "сломав" старую. Попробуем решить задачу индукцией по k! Докажем, что если утверждение выполняется при k-1, но оно выполняется и при k.

Подсказка 2

Если последовательность из 2k элементов удовлетворяет условию, то какой тогда будет эта последовательность без последнего пары a_k, b_k? Что будет с четностью N?

Подсказка 3

Нам подходят такие последовательности длины 2(k-1), где N четно, а_k = 0 и b_k = 1. А если N нечетно, то какой может быть пара (a_k;b_k)?

Показать доказательство

Применим метод математической индукции по параметру $k$ . При $k= 1$ формула очевидна. Докажем, что если она верна при $k − 1$ , то верна и при $k.$

Искомое число равно числу последовательностей

a1,b1,a2,b2,...,ak−1,bk−1,

(1)

в которых количество $i= 1,2,...k− 1,$ таких, что $ai = 0$ и $bi = 1$ четно (в этом случае пара $(ak,bk)$ может быть только $(0,1))$ плюс количество последовательностей вида (1) в которых количество чисел $i= 1,2,...k− 1,$ таких, что $ai = 0$ и $bi = 1$ нечетно, умноженному на 3 (так как пара $(ak,bk)$ может быть любой из пар $(0,0),(1,0),(1,1)).$ В итоге по предположению индукции нужное число последовательностей будет удовлетворять равенству

( ( )) ( ) 22(k−1)− 22(k−1)−1 − 2k−2 + 3 22(k−1)−1− 2k−2 =22k−1− 2k−1

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#68242

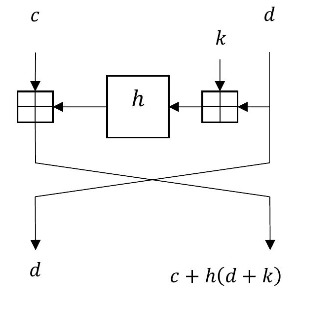
Имеется устройство, которое строит последовательность чисел $x,x ,x ,... 0 1 2$ следующим образом: первые два члена $x 0$ и $x 1$ мы задаем самостоятельно, а последующие члены устройство вычисляет так: $x2 =x0+ 13⋅(x1+ k1),x3 = x1+ 13 ⋅(x2+ k2),...$ Здесь $k1,k2,...$ — – некоторая фиксированная ключевая последовательность. При этом все числа $x0,x1,x2,...$ и $k1,k2,...$ являются целыми, лежащими в пределах от 0 до 32 включительно. (Если в процессе вычислений получится число, превосходящее 32, то результат будет заменен его остатком от деления на 33; например, $16+ 13 ⋅2 =9.)$ С помощью этого устройства построили две последовательности $a0,a1,a2,...$ и $b0,b1,b2,...,$ по первым членам $a0 =1,a1 = 3$ и $b0 =1,b1 =12.$ Верно ли, что найдётся ключевая последовательность $k1,k2,...$ и некоторое целое $t,$ большее 0, такие, что выполняются условия:

a) $bt = at,bt+1 =at+1?$

б) $bt = at+1?$

Решение обоснуйте.

Источники: Верченко-2023 (см. v-olymp.ru)

Подсказки к задаче

Пункт а), подсказка 1

У вас есть равенство двух членов одной последовательности двум другим. А как можно выразить, например предыдущий член последовательности через два соседних? Попробуйте так прийти к противоречию)

Пункт б), подсказка 1

Мы понимаем, что последовательности устроены одинаковым образом, так еще и ключевая последовательность у них одинаковая. Что можно сделать, чтобы вообще исключить эту последовательность?

Пункт б), подсказка 2

Вычесть одну последовательность из другой! По факту, в этой последовательности тогда нужно будет понять, есть там единица, или нет. В таком случае посмотрите на первые члены и на то, по какому модулю у нас все происходит и придите к противоречию)

Показать ответ и решение

а) Для всех $t≥1$

at+1 = at− 1+13(at+ kt),at−1 =at+1− 13(at+kt)

Поэтому, если $bt = at,bt+1 =at+1$ , то $bt−1 =at−1,...b1 = a1,b0 = a0$ , что противоречит условию.

б) Удобно перейти к разностям полублоков $zt = bt− at$ (везде далее действия с полублоками (умножение, сложение и вычитание) производятся по модулю $M$ ) и выяснить, может ли 1 появиться в ${z} t$ . Из уравнения шифрования

bt+1 = bt−1+ 13(bt+kt),t≥ 1

a =a + 13(a +k ),t≥ 1 t+1 t−1 t t

получаем после вычитания

zt+1 = zt−1+ 13zt,t≥1,

что последовательность разностей не зависит от ключа $kt$ . По условию $(z0,z1)= (0,9),(z0,z1,M )= 3$ , поэтому все члены последовательности будут делиться на $3$ , и единицы там не будет.

Ответ:

а) нет

б) нет

Ошибка.
Попробуйте повторить позже

Задача 3#71370

Знаками открытого и шифрованного текстов являются пары целых от 0 до 31. Для зашифрования используется секретный ключ $k$ (целое число от 0 до 31), заданная таблично функция $h,$ а также функция $g(c,d),$ которая паре целых чисел $(c,d)$ ставит в соответствие пару $(d,c+ h(d+k))$ (причем если число $d +k$ или $d+ h(d+ k)$ превышает 31 , то их заменяют остатком от деления на 32 $).$ Знак шифрованного текста $(b1,b2)$ получается из знака открытого текста $(a1,a2)$ путем 128-кратного применения функции $g :$

(b1,b2)= g128(a1,a2)= g(...g(g(a1,a2)))

Известно, что знак открытого текста $(21,0)$ преобразовался в знак зашифрованного текста $(15,25),$ знак $(7,3)$ преобразовался в $(29,5),(0,17)$ — в $(25,4)$ и, наконец, $(5,21)−$ в $(22,9).$ Найдите ключ $k.$


$i$	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20

$h(i)$	9	1	30	4	24	12	8	23	18	7	16	15	21	26	10	17	19	22	13	28	14


21	22	23	24	25	26	27	28	29	30	31

11	2	29	3	6	27	0	5	25	31	20

Источники: Верченко-2022 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Применять 128 раз одну и ту же функцию очень сложно...поэтому было бы хорошо, если мы сразу могли понимать, а что у нас получается на каждой итерации? Может ли в итоге у двух разных пар получиться один и тот же знак?

Подсказка 2

Если две пары отличаются одним применением функции, то и их знаки тоже отличаются одним применением функции. Как это связать с условием?

Подсказка 3

Попробуем найти такие пары чисел, которые удовлетворяют утверждению из подсказки 2. Теперь мы знаем, какие пары отличаются применением функции g! Несложно найти k)

Показать ответ и решение

Необходимо заметить, что из равенств

128 (b1,b2)= g (a1,a2)

( ′ ′) 128( ′ ′) b1,b2 = g a1,a2

(a′,a′)= g(a,a ) 1 2 1 2

следует равенство

(b′,b′)= g(b,b ) 1 2 1 2

Необходимым условием выполнения равенств $(a′1,a′2)= g(a1,a2),(b′1,b′2)= g(b1,b2)$ являются равенства $a′1 = a2,b′1 = b2.$ Среди приведенных в задаче пар знаков открытого и шифрованного текстов есть знаки, удовлетворяющие этому условию: одна пара $(21,0),(0,17)$ и вторая пара $(29,5),(5,21).$ То есть

(15,25)=g128(21,0)

(25,4)= g128(0,17)

Из условия задачи возможность найти ключ — воспользоваться равенствами

(0,17)= g(21,0), (25,4)= g(15,25)

Убедимся, что при этих условиях оба равенства дают одинаковое значение ключа $k.$

$PIC$

Получаем, что $k= 19.$

Ответ: 19

Ошибка.
Попробуйте повторить позже

Задача 4#71013

На вход устройства подается лента с записанными на ней нулями и единицами:

$PIC$

За один такт устройство считывает с ленты с позиций $μ1,μ2,μ3$ (на первом такте $μ1 = 1$ ) три значения $x,y,z$ . Если $x+ y+z ≥2,$ то устройство на новой ленте печатает 1 , иначе — 0 . Затем устройство сдвигается на одну позицию вправо, и процедура повторяется. Найдите разности $d1 = μ2− μ1$ и $d2 = μ3− μ2,$ если известно, что $d1 +d2 ≤ 10,$ а на новой ленте было напечатано следующее: $0001000010111111000111010111011010101001 ...$ (для примера на рисунке изображен случай $d1 = 3,d2 =5).$

Источники: Верченко-2022 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Да, можно и перебрать d_1 и d_2, но это будет долго) Попробуем сократить перебор! Что мы вообще умеем делать? Мы умеем брать конкретные элементы ленты и считать их сумму, если расстояния между ними это d_1 и d_2. Какие "удобные" элементы хочется взять?

Подсказка 2

Рассмотрим систему неравенств, которая соответствует выходных знакам вида 1...1 на расстоянии d_1. С помощью нее мы сможем дать ограничения на элементы, находящиеся на расстоянии d_1. Таким образом мы сможем перебрать и методом "пристального взгляда на ленту" найти d_1. Аналогично с d_2!

Показать ответ и решение

Число возможных вариантов $d 1$ и $d :10+ 9+ ⋅⋅⋅+1 =55 2$ , можно для каждого варианта проверять, что соответствие входных и выходных символов, а можно предложить более быстрый способ, заключающийся в нахождении сначала $d1$ (максимум 10 вариантов), а затем $d2$ . Для этого достаточно заметить следующее.