Комбинаторика на Верченко —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Комбинаторика на Верченко

Тема Межрегиональная им. И. Я. Верченко (криптография)

Комбинаторика на Верченко

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела межрегиональная им. и. я. верченко (криптография)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#68243

Для входа в университет Криптоландии у каждого студента есть карточка, на которой записана уникальная (у каждого студента своя) последовательность $x1,x2,x3,x4,x5,x6,x7$ из целых чисел от 0 до 5. При входе в университет студент прикладывает карточку к устройству, которое подсчитывает величины $A$ и $B$ по формулам:

A= ((x1 ∗x2)∗ x3)∗x4

B =(x5∘x6)∘x7

Операции $∗$ и $∘$ задаются таблицами (представляющими собой латинские квадраты: у них в каждой строке и каждом столбце числа не повторяются).

$PIC$

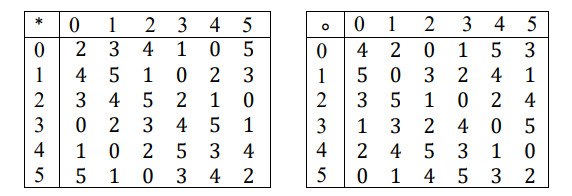
Например, $3∗2 =3,$ $2∘ 4=2.$ Студенту разрешат войти, если $A = B.$

Сколько самое большое может быть студентов в таком университете?

Подсказки к задаче

Подсказка 1

Делать вычисления по этим таблицам точно не хочется, поэтому давайте подумаем. Посмотрите внимательно на строчки и столбцы таблиц...что в них есть примечательного?

Подсказка 2

В каждой строчке и в каждом столбце по одному разу использовано каждое число от 0 до 6) Что это может значить?

Подсказка 3

Например, для любого x от 0 до 6 найдется такой y, что каждая из этих операций с x и y даст результат который мы хотим, причём y будет однозначно задаваться по таблице) Раскрутите эту идею.

Показать ответ и решение

Если код составлен из чисел от $0$ до $m − 1$ , то для каждого числа

k∈ {0,...,m − 1}

число последовательностей $x1,x2,x3,x4$ , для которых $A = k$ , равно $m3$ , так как при любых заданных $x1,x2,x3$ значение $x4$ определяется в этом случае однозначно.

Аналогично, число последовательностей $x ,x,x 5 6 7$ для которых $B = k$ , равно $m2$ . Тогда общее число последовательностей $x ,x,x ,x,x ,x ,x 1 2 3 4 5 6 7$ , для которых $A= B =k$ , равно $m3m2 = m5$ . Суммируя по $k$ от $0$ до $m − 1$ , получаем ответ: $m6$ .

Ответ:

$66$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#68240

Пароли в системе составляются из букв английского алфавита (26 букв) и цифр. При этом требуется, чтобы в пароле содержались цифра и заглавная буква. Пользователь допускается в систему, если предъявленный им пароль отличается от установленного не более чем в одном символе. Сколько паролей, соответствующих требованиям составления, позволят войти в систему, если для пользователя был установлен пароль Tw38dttf (не совпадающих с установленным паролем)?

Источники: Верченко-2023 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Посмотрите, сколько способов есть заменить маленький символ в пароле? А цифру? А заглавную букву? И помните про условие, что обязательно должна быть заглавная буква и цифра)

Показать ответ и решение

Раскладываем пароль "по слоям": цифра + заглавная + строчная и смотрим, какие ограничения есть по замене в каждой позиции. Цифр две, поэтому одну из них можно заменить произвольно на любой знак из $26+ 26+ 10 − 1= 61$ . Если менять заглавную T, то только на заглавную: $26− 1= 25$ вариантов. Строчные можно на любые, это ещё $5⋅61= 305$ вариантов. Итого $2⋅61+ 25+5 ⋅61 =452$ вариантов.

Ответ: 452

Ошибка.
Попробуйте повторить позже

Задача 3#71371

В Криптоландии используется алфавит, состоящий из четырёх латинских букв $a,b,c,d.$ Любая последовательность букв алфавита будет словом криптоландского языка при выполнении единственного ограничения: если в последовательности есть хоть одна буква " $a$ то тогда в ней обязательно должны встретиться две буквы " $a$ "подряд.

Например, последовательности $baacda,aabb,ddd$ являются словами, а последовательности $bcadda,abba$ — не являются. Найдите число слов длины 8 в криптоландском языке.

Источники: Верченко-2022 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Всего существует 4⁸ последовательностей длины 8, составленных из букв криптоландского алфавита. Подумайте, как удобнее всего почитать число тех последовательностей, которые являются словами.

Подсказка 2

Все последовательности разбиваются на три непересекающихся множества: 1. Не содержащие буквы a; 2. Содержащие букву а и хотя бы одну пару аа; 3. Содержащие букву а и не содержащие ни одной пары аа. При этом очевидно, что элементы 1 и 2 множеств являются словами, а 3 - нет. Посчитать число элементов второго множества выглядит либо очень сложной задачей, либо вовсе нереальной. Тогда удобнее всего найти число последовательностей, являющихся словами, будет просто вычтя из 4⁸ число элементов 3 множества. Подумайте, каким образом их можно сосчитать.

Подсказка 3

Для n букв а в слове возможно найти число способов расставить их в последовательности длины 8 по формуле: число сочетаний из 8+1-n по n. Кроме того у нас есть еще 3^(8-n) способов расставить b, c, d на оставшиеся места. Подумайте, какое максимально значение может принимать n.

Подсказка 4

При n ≥ 5 гарантировано будет существовать пара aa. Значит, они нам не подходят. Теперь найдем число последовательностей для n = 1, 2, 3, 4, сложим их и таким образом получим количество элементов 3 множества.

Показать ответ и решение

Множество всех последовательностей длины $8$ состоит из $48$ последовательностей. Это множество разбивается на три непересекающихся между собой подмножества:

1.: Последовательностей, не содержащих $a.$
2.: Последовательностей, содержащих $a,$ но не содержащих двух подряд идущих таких букв.
3.: Последовательностей, содержащих $a$ , в которых встречаются две подряд идущие такие буквы.

Чтобы решить задачу, нужно найти число последовательностей во втором подмножестве и вычесть его из числа $48.$

В свою очередь, множество последовательностей второго типа можно разбить на непересекающиеся подмножества, в которые входят последовательности, содержащие $1,2,3,4$ букв " $a$ ".

Поскольку число последовательностей длины $8$ , содержащих ровно $t$ отдельно стоящих букв $a$ , равно $Ct8+1−t(4− 1)8−t,$ то общее число последовательностей второго типа будет равно

4∑ t 8−t C9−t3 =38070 t=1

В итоге получаем

48 − 38070 =27466

Ответ: 27466

Ошибка.
Попробуйте повторить позже

Задача 4#71012

Петя использует для работы в интернете пароли из шести символов. Опасаясь злоумышленников, он решил в каждом пароле изменить порядок следования символов, используя для этого одно и то же правило, которое записал в книжечку. Правило могло выглядеть, например, так:

( ) 1 2 3 4 5 6 3 6 4 5 1 2

То есть первый символ ставится на третье место, второй - на шестое и так далее. В своем пароле для почты qwerty Петя переставил буквы по правилу из книжечки, а затем, для большей надежности переставил буквы по этому же правилу еще раз. (Если использовать правило как в примере, то из qwerty после первой перестановки получится tyqerw, а после второй — rwtqey).

a) Какие из нижеследующих комбинаций


yetrqw	eyrtqw	yrwteq	rewqyt	qwtyre	tywreq

могли быть получены двойной перестановкой букв в пароле qwerty? (используя, возможно, другие правила указанного вида)

б) Петя потерял книжечку! Он помнит, что первоначально пароль был qwerty, но правило, по которому были в нём дважды переставлены буквы, не помнит. За какое наименьшее число попыток можно с гарантией подобрать утерянный пароль?

Источники: Верченко-2022 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

В этой задачи нам описали какой-то алгоритм и просят понять, что могло быть результатом этого алгоритма. В таких задачах полезно поискать инварианты (то, что не меняется в результате работы алгоритма) или свойства: как данный алгоритм работает для некоторых схожих входных данных. Обратите внимание на то, что в алгоритме как бы описаны взаимодействия между объектами: символ с места A переходит в символ с местов B, а какой математический объект позволяет нам показывать связи между объектами?

Подсказка 2

Правильно, можно использовать граф, попробуйте нарисовать его для правила из "примера", а затем для двойной перестановки и посмотрите, как он изменился. Если не сразу понятно, на что обращать внимание, то придумайте своё правило для перестановки чисел и проделайте те же действия.

Подсказка 3

Можно заметить, что циклы длины 2n распадаются на 2 цикла длины n, а каждый цикл длины 2n+1 остаётся длины 2n+1 (взаимосвязи между объектами другие, но длина та же). Ага! Из каждого объекта при какой-то операции получается по 2 объекта, на что это похоже?

Подсказка 4

Попробуйте сформулировать аналог леммы о рукопожатиях (граф имеет чётное число вершин нечётных степеней), но для циклов, подумайте для циклов какой длины утверждение становится более сильным, а для какой не несёт никакой информации, из циклов какой длины можно получить циклы другой длины?

Подсказка 5

Верно, если мы посмотрим, что происходит с циклами длины 2 * (2n+1) (длина которых делится на 2, но не делится на 4), то они просто превращаются в нечётные циклы, а так как мы не знаем, сколько изначально было циклов нечётной длины, то про их итоговую чётность мы ничего сказать не можем. Почему бы тогда не посмотреть на циклы чётной длины, ведь они могут получиться только из циклов кратных 4. А сколько тогда циклов чётной длины будет?

Подсказка 6

Да, циклов чётной длины чётное количество, иначе бы не выполнялось утверждение о том, что из циклов длины 2n получаются 2 цикла длины n. Осталось посмотреть, какие из перестановок из пункта "а" противоречат данному утверждению, а для остальных найти пример!

Подсказка 7

Давайте сразу определимся, что "за n попыток можно с гарантией подобрать пароль" значит, что какие бы случайные n попыток мы не сделали, хотя бы одна из них даст нам наш пароль. Понятно, что тогда надо посчитать общее количество двойных перестановок, оно и будет ответом. Остаётся только понять, что на самом деле мы доказали критерий существования двойных перестановок (Двойная перестановка существует тогда и только тогда, когда циклов чётной длины чётное количество, попробуйте показать, почему это работает и в обратную сторону).

Подсказка 8

Попробуйте разбить подсчёт на более простые случаи. Если всего 6 элементов в графе, то сколько циклов и какой длины может быть при условии, что это двойная перестановка? Всегда при подсчёте задавайте себе вопросы: а важен ли порядок? А есть ли граничные случаи и все ли их я рассмотрел?

Показать ответ и решение

Приведенное в условии правило перестановки букв, или перестановку, будем обозначать греческой буквой $σ.$ Перестановку $σ$ можно интерпретировать как отображение множества цифр ${1,2,3,4,5,6}$ в себя. Например, тот факт, что первая буква перешла на третье место, можно записать как $σ(1)= 3,$ а также изобразить стрелочкой из 1 в 3:

$PIC$

Видно, что если бы мы перестановку $σ$ применяли многократно, то буквы на 2-й и 6-й позициях постоянно менялись бы местами, а буквы на позициях 1, 3, 4, 5 переставлялись бы по циклу. Поэтому перестановка $σ$ может символически быть записана в виде произведения циклов:

( ) σ = 1 2 3 4 5 6 = (1345)(26)= 4∗2 3 6 4 5 1 2

Запись $4∗ 2$ отражает цикловую структуру перестановки $σ,$ показывая, что в ней один цикл длины 4 и один цикл длины 2.

Посмотрим теперь более детально на то, что произойдет, если по правилу $σ$ переставить буквы еще раз. Так 1 при первом применении правила $σ$ перешла в 3: $σ(1)=3,$ а при повторном применении 3 перешла в 4: $σ(3)= 4.$ Значит, в результате двойной перестановки 1 переходит в 4. Будем это записывать как $σ(σ(1))= 4$ или же $2 σ (1) =4.$ Поэтому правило двойной перестановки букв, представляющее собой квадрат перестановки $σ,$ выглядит так:

$PIC$

Заметим, что после повторной перестановки 2 и 6 вернутся на свои места, то есть цикл $(2,6)$ распадется на два тривиальных цикла $(2)$ и $(6),$ а цикл $(1345)$ превратится в два цикла $(1,4)$ и $(3,5).$ Таким образом, при повторном применении перестановки циклы четной длины $2n$ распадаются на два цикла, длины $n$ каждый. Несложно проверить, что при этом циклы нечетной длины сохраняются. Справедливо утверждение.

Утверждение. Перестановка представляет собой полный квадрат в том и только том случае, когда в ее представлении в виде произведения непересекающихся циклов может быть сколько угодно и какие угодно циклы нечётной длины, в то время как циклов одной и той же чётной длины должно быть чётное число.

Рассмотрим первую комбинацию уеqwrt из пункта а). Она получена из qwerty перестановкой $( ) 1 2 3 4 5 6 = (1324561), 3 4 2 5 6 1$ которая представляет собой цикл длины 6. Поскольку циклов четной длины здесь нечетное количество (всего один), то, согласно утверждению, такая комбинация двойной перестановкой букв получиться не могла. Аналогично исследуются и остальные комбинации в пункте а).

Проведем подсчет общего числа перестановок, являющихся полными квадратами. Их цикловые структуры могут быть следующие:

$1∗ 1∗1∗1∗ 1∗1.$ Это перестановка, оставляющая все на своих местах (тождественная перестановка). Она единственна.
$1∗ 5.$ Мы должны выбрать 5 элементов из шести, чтобы составить цикл дины 5. Это можно сделать 6-ю способами. Из пяти элементов цикл длины 5 можно организовать $(5− 1)!$ способами (действительно, организуем цикл из пяти элементов $a1,a2,a3,a4,a5;$ элемент $a1$ может перейти в любой из четырех (т.к. в себя нельзя), элемент $a2$ переходит в один из оставшихся трех и т.д. В итоге получаем $4 ⋅3 ⋅2 ⋅1$ способов). Таким образом, здесь $6⋅4!= 144$ перестановок.
$2∗ 2∗1∗1.$ Выбрать два элемента из шести для первого цикла длины 2 можно $2 C6$ способами. Для второго цикла длины 2 есть $2 C4$ способа. Итого $2 2 C 6 ⋅C4 = 90.$ От порядка следования циклов результат не зависит, поэтому 90 еще следует разделить на два. Всего 45 перестановок с такой структурой.
$3∗ 3.$ Здесь мы 6 элементов десятью способами $( ) 12C36 = 10$ разбиваем на две тройки и из каждой тройки получаем по 2 цикла. Всего 40 перестановок.
$3∗ 1∗1∗1.$ Здесь мы двадцатью способами $( ) C36 = 20$ выбираем тройку и из каждой тройки получаем по 2 цикла. Всего 40 перестановок.