Для наглядности представим себе карту нашего города в виде графа, в которой улица - это ребро такого квадратика.

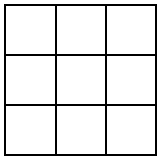
Ясно, что нам нужно обойти все улицы. В самом лучшем случае, то есть в том случае, если бы нам удалось обойти весь граф, пройдя каждое ребро лишь один раз, у нас получилось бы метров. Но можем ли мы так сделать? То есть, иными словами, будет ли наш граф эйлеровым?

Заметим, что у нас есть целых 8 вершин степени 3. А это слишком много. Эйлеров граф может содержать либо 0, либо 2 вершины нечетной степени. Следовательно, наш граф - не эйлеров, и поэтому не получится обойти его весь, пройдя по каждому ребру лишь один раз - наш идеальный случай с 7200 метрами недостижим.

Эти 8 вершин степени 3, они плохие. Ведь мы должны начать и закончить в левой нижней точке нашего города, то есть эти 8 вершин степени 3 будут промежуточными.

А промежуточная вершина нашего потенциального пути, проходящего по всем ребрам лишь один раз, не может иметь нечетной степени. В промежуточную вершину мы должны зайти столько же раз, сколько и выйдем из неё.

Следовательно, каждая из этих 8 вершин степени 3 даст обязательно какое-то ребро, по которому мы пройдем дважды. И что же. получается, будет еще 8 лишних проходов?

Нет, не обязательно. Соседние вершины степени 3 могут давать один и тот же лишний проход - так можно сэкономить и сделать лишь 4 лишних прохода, а вот дальше уже сэкономить, очевидно, никак нельзя. Таким образом, получается 4 лишних прохода, поэтому наша оценка получилась такой:

Но это лишь оценка, а вдруг и такого пути не существует, но уже по каким-то другим, более тонким причинам?

На самом деле, существует, и сконструировать его не так-то сложно

В полном графе на 2024 вершинах будет

ребер.

А сколко же ребер будет в минимальном его связном подграфе? Более-менее ясно, что минимальный связных подграф получится, если мы оставим просто змейку из 2024 вершин, соединенных 2023 ребрами

Ведь если из такого графа удалить любое ребро, то он уже перестанет быть связным.

Таким образом, исходно у нас было 2047276 ребер, а должно остаться 2023 ребра. Следовательно, удалить нужно

ребра.

a) Да, существует, например:

b) Нет, потому что здесь получается 3 вершины нечетной степени, а по лемме о рукопожатиях вершин нечетной степени должно быть четно;

c) Нет, потому что у нас всего 8 вершин, а, значит, поскольку по нашему определению графа запрещены кратные ребра и петли, то в графе из 8 вершин максимальная степень вершины может быть 7 - когда она соединена со всеми остальными. А уж 8 не может быть никак;

d) Нет, потому что у нас 8 вершин и из них 2 вершины степени 7, то есть есть 2 вершины, соединенные со всеми остальными. В частности, есть 2 вершины, соединенные с первой вершиной. Поэтому у неё уже никак не может быть степень 1.

Связный граф эйлеров, если в нём 0 или 2 вершины нечетной степени. В противном случае, граф будет неэйлеровым.

В полном графе из вершин степень каждой вершины равна . То есть, если - чётно, то - нечётно, и в случае получается, что у нас вершин нечётной степени, и тогда граф неэйлеров.

Если же , то получаем отрезок между двумя точками, который, очевидно, эйлеров.

А если и, наоборот, - нечётно, то - чётно, и поэтому у нас все вершины чётной степени, значит, такой граф эйлеров (очевидно, он связен).

a) В этом графе все вершины чётной степени (2), а, следовательно, он эйлеров.

b) В этом графе все вершины чётной степени (4), а, следовательно, он эйлеров.

c) В этом графе есть три вершины степени 3, следовательно он не эйлеров.

Пусть - несвязен. Иначе, если он связен, то мы всё доказали.

Рассмотрим любые две вершины в .
1 случай. Если и в лежали в разных компонентах связности, то есть если их нельзя было соединить никаким путём в , то, в частности, в их не соединяло ребро. Но тогда в вершины и соединены ребром по определению. Следовательно в из можно попасть в .

2 случай. Если и лежали в одной и той же компоненте в . Но, по предположению, граф - несвязен. То есть, у него есть ещё хотя бы одна, другая компонента, которой и обе не принадлежат. Возьмём тогда любую вершину из другой компоненты, которой не принадлежат и . Тогда и нельзя соединить никаким путём в , и и - тоже нельзя соединить никаким путём в . В том числе, и не соединяются ребром в и и - тоже не соединяются ребром в . Но тогда по определению и соединены ребром в и и соединены ребром в . Следовательно, в можно из попасть в , пройдя по маршруту .

В любом случае получили, что произвольные в можно соединить путём. Следовательно, граф получается связным.

Представим себе граф, в котором вершины - это города, и 2 вершины соединены ребром, если два города, им соответствующие, соединены авиалинией.

Рассмотрим компоненту связности, в которую входит столица. Если в эту компоненту связности не входит очень маленький город (т.е. если из столицы в него нельзя долететь даже с пересадками в средних городах), то в его компоненту входит только он и какие-то средние города. Но тогда в связной компоненте столицы только 1 вершина нечётной степени (столица), а остальные - чётной (средние города). Противоречие с леммой о рукопожатиях. Ведь связная компонента столицы - это тоже какой-то граф. А в графе не может быть нечетного количества вершин нечётной степени. Следовательно, очень маленький город, имеющий степень 1, обязан быть в компоненте связности столицы.

a) На первый взгляд, компонент связности здесь 3. Но если приглядеться, то их четыре. Левый подграф нашего графа действительно связен и его нельзя расширить ни до какого большего связного подграфа. То же верно и про граф сверху справа. А вот снизу справа на самом деле есть только 2 отрезка - в их пересечении никакой вершины нет. Поэтому объединение этих отрезков связным не будет - мы не сможем попасть из одного отрезка в другой. Следовательно, справа внизу нарисовано две компоненты, а не одна. Получается, всего 4 компоненты связности.

b) То же самое, что и в пункте a) - здесь на самом деле 3 компоненты, потому что сверху треугольник и прямоугольник образуют две различные компоненты связности - мы никак не можем по рёбрам попасть из треугольника в прямоугольник и наоборот. Несмотря на то что на картинке они пересекаются, по сути их можно было бы нарисовать и непересекающимися. Общих вершин у них нет. Поэтому ответ здесь - 3 компоненты.

c) Тут ясно, что данный граф связный, то есть у него одна компонента связности.

Будем рассматривать только рёбра, соединяющие вершины разных цветов. Пусть — количество синих вершин, а — число зелёных вершин. Так как каждая синяя вершина соединена с зелёными, то число рёбер, соединяющих разноцветные вершины, равно . С другой стороны, так как каждая зелёная вершина соединена с 9 синими, то число рёбер, соединяющих разноцветные вершины, равно . Но мы посчитали количество разноцветных вершин двумя способами, но от способа подсчёта оно зависеть не должно. Тогда получаем равенство , из которого ясно, что , то есть зелёных вершин больше.

Представим себе граф, вершинами которого будут города в этом государстве, и две вершины соединены в графе, если соответствующие города соединены в государстве.

Пусть всего у нас в этом государстве городов. Тогда , потому степень каждой вершины равна 5. С другой стороны, по лемме о рукопожатиях, , поскольку дорог у нас 2013 по условию.

Имеем уравнение

Тогда . И мы видим, что целым быть не может. Противоречие. Значит, это невозможно.

Допустим, такой граф бы существовал. Но раз у первых четырех вершин степени равны 4, а вершин всего 5, то это означает, что первые 4 вершины соединены со всеми остальными. Но тогда и последняя пятая должна быть соединена со всеми остальными. Следовательно, её степень не может быть равна 2. Противоречие.

В полном графе каждая вершина соединена с каждой. Но при этом мы считаем, что в полном графе вершины не соединены сами с собой. Поэтому его матрица смежности будет состоять вся из единиц, кроме главной диагонали. На главной диагонали будут стоять нули.