Рассмотрим в нашем квадрате квадратов

Назовём их выделенными.

Заметим, что если одна клетка некоторого диполя принадлежит какому-то выделенному квадрату, то другая клетка этого диполя принадлежит (соседнему) выделенному квадрату.

На рисунке отмечены номерами клетки в выделенных квадратах, так что у любого диполя обе клетки должны иметь один и тот же номер. Но клеток с данным номером (например, с номером ) девять, и поэтому при “распределении” клеток с номером по диполям по меньшей мере одна клетка окажется нераспределённой (лишней). Таким образом, для каждого из четырех номеров остаётся нераспределённой минимум одна клетка среди выделенных квадратов, а значит, всего имеется минимум нераспределенные клетки.

Получаем оценку: максимальное число непересекающихся диполей во всём квадрате не больше

Построим теперь пример на диполей. Для этого “отрежем” левый нижний выделенный квадрат. Останется клетчатая фигура из клеток, которая разбивается на квадрат и два прямоугольника и . Эта фигура полностью разбивается на диполи, поскольку любые последовательные клеток строки или столбца, очевидно, разбиваются на три диполя.

Обозначим

Тогда . Возведем в квадрат

В случае или получаем, что левая часть равенства рациональна, а значит и правая тоже, то есть или . Если имеет место случай , то

В случае же (не умаляя общности ) получаем

И так как , равенство возможно только в случае . И тогда также То есть если или , то требуемое верно.

Пусть теперь . Преобразуем:

Равенство возможно только в случае, если справа рациональное число, то есть . Тогда получаем следующую систему

Эта система имеет вид

По следствию теоремы Виета и являются корнями уравнения . Но у квадратного уравнения максимум корня, поэтому либо и , либо и .

В первом случае получаем , что невозможно, кроме разобранного случая

Во втором случае , также невозможно, если

(a) Решим неравенство относительно замены

То есть

В случаях и в первой четверти получаем часть плоскости под графиком , а в третьей четверти часть плоскости над этим графиком.

В случае во второй четверти неравенству удовлетворяет часть плоскости под графиком , а в четвертой — часть плоскости над этим графиком.

(b) Приведем явный алгоритм соединения двух точек получившегося множества . Будем соединять любые две точки и через точку . Для этого надо показать, что любая прямая, соединяющая точку множества и , лежит в множестве. Заметим, что при приближении из в по прямой произведение по модулю уменьшается, а значит, если точка из множества, то и прямая из нее в тоже. Тем самым показали, что соединять и можно соединением с и c

Линейное по выражение при . Рассмотрим тригонометрическую окружность. Если , то решению соответствует точки на окружности, по на каждой полуокружности, которых всего , так как аргумент принимает значения из . Итого решений.

Если , то подходят точки вида . То есть решений в этом случае.

Если , то на каждой полуокружности подходит по одной точке вида . То есть решений всего.

Пусть Обозначим через точку пересечение и . Тогда, если радиус окружности равен , то из прямоугольного треугольника

Выразим из прямоугольного треугольника

Подставляя в , получаем

как угол треугольника.

(a) Начертим граф возможных соседей. Рассмотрим три пары вершин в четырехугольниках на графе (они отмечены жирными точками), а именно: (2, 10), (1, 9) и (3, 11) – это вершины с наименьшей степенью (количеством соседей), равной 2. Предположим, от противного, что есть простой путь на графе (т.е. без повторения вершин), проходящий через все вершины. Тогда найдется такая пара вершин среди трех указанных пар, что путь не начинается и не кончается в вершинах из этой пары (такая пара есть, т.к. концов у пути – два, а пар – три). Таким образом, обе вершины этой пары – “проходны”, но если впервые будет пройдена одна вершина из этой пары, то вторая вершина станет изолированной («отрезанной»: в неё нельзя будет попасть потом). Противоречие.

(b) Пример перестановки: 2, 5, 10, 7, 12, 9, 4, 1, 6, 3, 8, 11. Граф (см. рисунок) помогает построить подобный пример.

Поскольку у параллелепипедов ребра соответственно параллельны, мы можем ввести декартову систему координат, направив оси вдоль трех ребер, смежных с одной вершиной (которая станет началом координат) выбранного параллелепипеда. В этой системе координат ребра всех параллелепипедов будут параллельны осям. Спроектировав на ось Ох данный -ый параллелепипед получим отрезок, который обозначим Любая пара таких отрезков имеет непустое пересечение (в противном случае соответствующая пара параллелепипедов не пересекается).

Таким образом, приходим к такой задаче: на числовой прямой есть попарно пересекающиеся отрезки и требуется доказать, что у них имеется общая точка. Опытные олимпиадники могут сразу сослаться на теорему Хелли. Мы же приведём её доказательство, чтобы не оставлять у неопытных читателей чувство неловкости.

Пусть – наибольшее значение среди левых концов отрезков, т.е. и аналогично, пусть — наименьшее значение среди правых концов отрезков. Тогда так как в противном случае для некоторых и а значит, -ый и -ый отрезки не пересекаются. Отсюда следует, что любая точка отрезка будет общей для всех наших отрезков. Итак, пусть точка принадлежит проекциям на ось Ох всех параллелепипедов. Точно так же мы можем найти общие точки и проекций на оси Oy и Oz. Тогда точка с координатами будет принадлежать всем параллелепипедам.

Заметим, что отсюда нетрудно видеть, что является решением. Далее покажем, что функция в левой части строго возрастает на всей числовой прямой. Действительно, мы видим разность возрастающей (основание больше 1) и убывающей (основание меньше 1) показательных функций, которая строго возрастает. Отсюда равенство имеет не более одного решения, которое уже было найдено.

Первое решение.

Так как

то неравенство верно для любого поскольку тогда

Второе решение.

Как известно, откуда Осталось показать, что

То есть неравенство выполнено для всех

Первое решение.

Введём длины сторон, как — площадь, — полупериметр. Далее воспользуемся формулами откуда

Для углов известно зная это, распишем произведение

Осталось воспользоваться теоремой косинусов. Например, для угла имеем

То есть косинусы также рациональны, откуда следует рациональность произведения.

Второе решение.

а)

Мы знаем, что где — площадь треугольника, а — его полупериметр. С другой стороны, где — стороны треугольника. Тогда

Следовательно,

По формуле Герона

Тогда

Заметим, что здесь каждый из множителей рационален, а следовательно и отношение рационально.

б) Запишем теорему синусов:

Отсюда получаем

Пусть — точка пересечения биссектрис треугольника Рассмотрим треугольник и запишем для него теорему синусов:

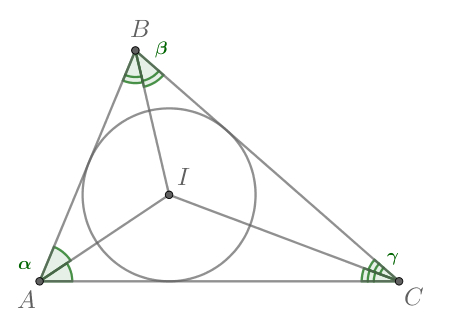
Подставим распишем синус двойного угла и синус суммы, получим

Отсюда получаем

Аналогично

Заметим, что

Таким образом,

Тогда

По предыдущему пункту рационально, значит и рационально.

Пусть — данный прямоугольник. Без ограничения общности можно считать, что — начало координат: иначе сместим начало координат в точку а в конце сделаем сдвиг на целочисленный вектор Обозначим векторы где , — целые числа. Поскольку и взаимно перпендикулярны, их скалярное произведение равно нулю, т.е. (этот факт также следует из соотношения для угловых коэффициентов перпендикулярных прямых и ).

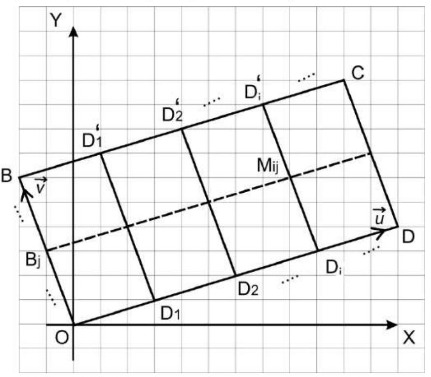
Рассмотрим сначала случай, когда и не взаимно просты. Тогда НОД( В этом случае рассмотрим на стороне промежуточные точки где Проведём через точки прямые, параллельные стороне Они пересекут сторону в точках где

Таким образом, точки и имеют целочисленные координаты и тем самым, прямые разбивают прямоугольник на прямоугольников с целочисленными вершинами. Назовем это разбиением первого типа.

Аналогично, если и не взаимно просты, то прямыми, параллельными стороне разобьем на меньшие прямоугольники с целочисленными вершинами. Назовем это разбиением второго типа; прямые этого разбиения проходят через промежуточные точки на стороне где а — наибольший общий делитель и Заметим, что в случае, когда одновременно и прямые первого и второго разбиений разбивают прямоугольник на равных прямоугольников с вершинами в точках где т.е. все вершины имеют целочисленные координаты.

Итак, приходим к случаю, когда координаты каждого из векторов взаимно просты. Но тогда из равенства получим, что (действительно, из этого равенства следует, что делится на и, в то же время, делится на значит, аналогично, с учетом знака в данном равенстве). В этом случае стороны прямоугольника равны: и наш прямоугольник квадрат.

Возьмем пифагорову тройку, например, и будем рассматривать соотношения

для различных натуральных Если положить

то взяв число делящееся на 5, т.е. для натурального получим

Таким образом, при любом натуральном числа вида где и удовлетворяют исходному уравнению.

Сначала исследуем ОДЗ переменных. Поскольку

то Аналогично, Таким образом, для неотрицательных обе части неравенства имеют смысл и неотрицательны. Поэтому возведение в квадрат обеих частей приводит к равносильному выражению, которое, (после сокращения) запишется так:

После возведения в квадрат и уничтожения подобных членов оно примет вид:

Второе выражения это верно, т.к. и

Значения и при любом как известно, связаны соотношением

Таким образом, требуется исследовать функцию

где Данная квадратичная функция с отрицательным старшим коэффициентом принимает наибольшее значение в точке (вершине параболы), равное Наименьшее значение принимается на границе промежутка а именно, в точке и оно равно (на другом конце промежутка, при значение равно нулю). Соответствующие значения в которых достигаются наибольшее и наименьшее значения функции, таковы: и

Пусть Тогда по условию

После обратной замены

Рассмотрим многочлен

Во-первых, его старший коэффициент равен Это меньше Покажем теперь, что во всех целых точках он принимает целые значения. В числителе находится произведение десяти подряд идущих целых чисел. Докажем, что оно делится на каждый множитель знаменателя.

Делимость на Среди десяти подряд идущих целых чисел есть пять чётных. Из этих пяти хотя бы одно делится на хотя бы одно — на То есть числитель всегда делится на

Делимость на следует из того, что среди десяти подряд идущих целых чисел есть хотя бы два, кратных Аналогично получаем делимость на

Делимость на Среди десяти подряд идущих чисел есть хотя бы три, делящихся на притом одно из них делится на отсюда получаем делимость.

Первое решение.

Вспомним следующую конструкцию: проведем две перпендикулярные прямые и на одной из них отметим точку, из которой отложим два равных угла, получив прямоугольный треугольник. Тогда где и — отрезки, на которые проведенная биссектриса делит сторону треугольника. Это следует из свойства биссектрисы: пусть — гипотенуза, — катет, тогда и так как получаем Также проведем медиану из отмеченной точки. Она будет пересекать катет выше биссектрисы в силу

По свойству точки пересечения медиан, . Пусть . Отметим — середину , тогда .

Проведем биссектрису угла . По сказанному ранее (биссектриса пересечет в точке, которая находится ниже — середины )

Треугольник — тупоугольный, поэтому так как опирается на тупой угол. Проведем биссектрису угла . Она пересечет ниже, чем точка — середина Поэтому

Итого получаем

То есть

Складывая, получаем

Второе решение.

Пусть — медиана равнобедренного треугольника , проведенная к основанию , тогда отрезок перпендикулярен основанию по свойству равнобедренного треугольника. По свойству точки пересечения медиан, . Обозначим и . Тогда неравенство равносильно неравенству . Последнее неравенство очевидно в случае, когда , так как

Пусть теперь . Из прямоугольного треугольников и имеем: , , значит, . Так как углы и лежат в интервале , то неравенство равносильно неравенству , то есть .

Рассмотрим разность

Так как , то и , и, значит,

следовательно, .

На прямой, проходящей через точку и перпендикулярной прямой , возьмем такую точку , что (она лежит на серединном перпендикуляре к . Тогда , поэтому . Отсюда следует, что точка лежит на окружности, проходящей через и , с центром в точке . Действительно, для этой окружности - центральный, а -вписанный (если бы точка лежала вне этой окружности, то был бы меньше половины центрального, а если бы точка С была внутри окружности, то был бы больше половины центрального).

Сделаем замену: Получим, уравнение:

Заметим, что является корнем и разделив уравнение на получим следующее:

Многочлен также имеет корень После деления этого многочлена на получаем уравнение:

Многочлен имеет только положительные коэффициенты и поэтому у него нет неотрицательных корней. Таким образом, единственный корень (кратности ) и, возвращаясь к переменной получаем два корня

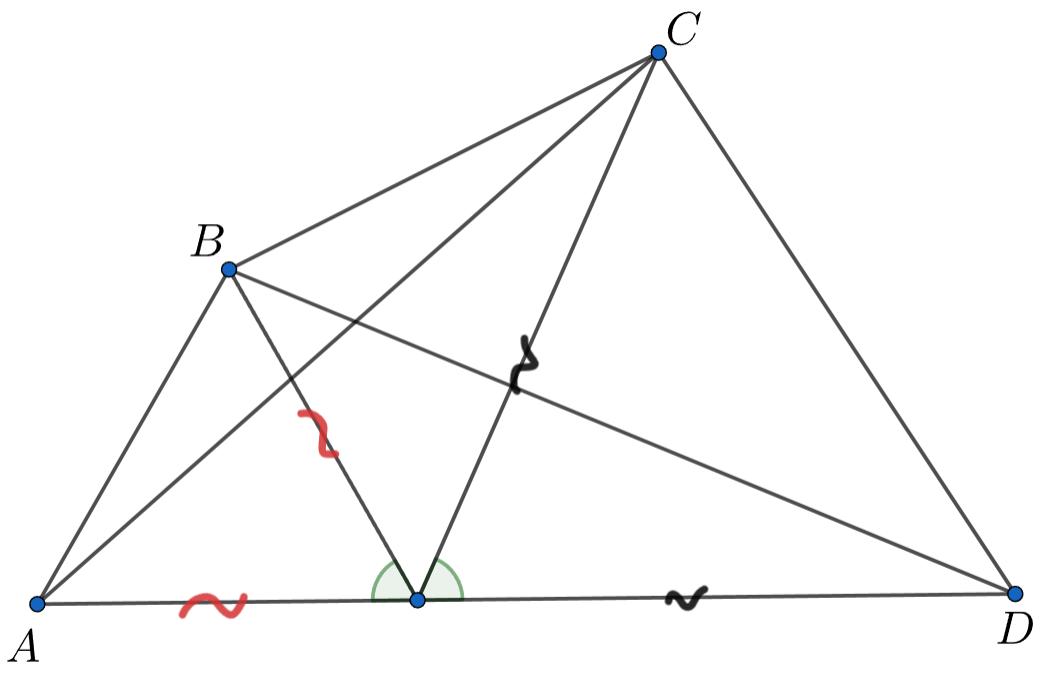
Сделаем поворот в точке на угол Заметим, что треугольник перешёл в треугольник Значит, эти треугольники равны. Следовательно, их высоты, проведённые к и равны.