Ошибка.
Попробуйте повторить позже
У вредного Васи есть клетчатая полоска длины 13 клеток и лента длины клеток, каждая шириной в одну клетку. Вася хочет
разрезать полоску на кусочки произвольной длины из нескольких целых клеток по своему усмотрению, а затем уложить часть из них на
ленту в некотором порядке так, чтобы в какой-то момент осталось не менее одного кусочка, ни один из которых уложить уже нельзя. При
этом кусочки укладываются строго по клеткам и не могут выходить за пределы ленты, ни одна клетка не должна быть накрыта ими
дважды и, если на ленте есть место, куда можно уложить очередной кусочек, Вася должен уложить его в одно из таких мест по своему
выбору. При каком минимальном N, как бы Вася ни старался, ему не удастся задуманное, то есть придётся уложить все
кусочки?
Источники:
Подсказка 1
Давайте попробуем себе немножко упростить задачу и посмотреть на финальный шаг, когда Вася не может уложить ни один из своих кусков, можно ли как-то без ограничения общности заменить их?
Подсказка 2
Да, давайте скажем, что в конце у Васи остался ровно 1 кусок длины x, и он положил до этого k отрезков. Давайте тогда попробуем как-то оценить N, интуитивно должно казаться, что длина каждого из k кусочков должна быть как можно меньше, и они должны выступать в качестве ограничителей для нашего кусочка x.
Подсказка 3
Если всё ещё не получается получить оценку, то не расстраивайтесь и подумайте, какое наибольшее расстояние может быть между двумя соседними кусочками, чтобы между ними не поместился кусок x, а сколько таких промежутков, куда можно в теории положить x (не забудьте, что лента по краям тоже ограничена), а также не забудьте про сами k кусочков, они тоже занимают место на ленте.
Подсказка 4
Мы получили, что N ≤ (x-1)(k+1) + (13-x) ≤ 48, остаётся только придумать пример, когда N=48 (потому что для меньших свойство о непокрываемости), и радоваться решённой задаче!
Заметим, что если в какой-то ход Васи осталось больше одного кусочка, а оставшиеся поместить нельзя, то можно рассмотреть разрезание, где все эти кусочки объединяются в один, а другие выкладываются на ленту тем же образом. Понятно, что такой кусок-склейка также не будет помещаться.
Значит, можно без ограничения общности предположить, что у Васи должен остаться ровно один кусок, который нельзя
поместить. Пусть его длина , а количество положенных кусочков равно
. Тогда
, при этом длина полосы
, так как
- количество клеточек занятых остальными кусочками, а
- количество ’зазоров’, в
которые теоретически мы могли поместить кусок длины
, но он не поместился, так как размеры зазоров не превосходят
.
Тогда Вася достигает своей цели при
То есть если , то Вася не сможет выполнить задуманное.
А при Васе достаточно разрезать полоску на
кусков размера
и
кусок размера
, при этом расположить
кусков
размера
он должен на расстояний не более
клеток друг от друга и от концов. (Чего он сможет достичь, так как
)
Ошибка.
Попробуйте повторить позже
Биссектриса угла параллелограмма
пересекает сторону
и продолжение стороны
за точку
в точках
и
соответственно, как показано на рисунке:
![]()
Доказать, что центр описанной окружности треугольника лежит на описанной окружности треугольника
.
Источники:
Подсказка 1
Когда в параллелограмме проведена биссектриса, так и хочется поискать равнобедренные треугольники. Видно, что △KCM — равнобедренный. С чем тогда хочется соединить центр О описанной окружности △KCM?
Подсказка 2
Верно, с точкой C! Тогда OC будет серединным перпендикуляром к KM. Но ведь не любая точка на нём будет центром окружности, поэтому надо как-то еще попользоваться ей. Предлагаю отметить, что OK=OC. А как нам подобраться к описанной окружности △BCD?
Подсказка 3
Можно попытаться доказать, что уголочки ∠OBC и ∠ODC равны. Какие у нас есть для этого инструменты? В самом удачном случае мы просто найдем равные треугольнички... У нас уже есть равенство отрезков OK и OC, поэтому можно попытаться установить равенство △BOK и △DOC...
Подсказка 4
Равенство сторон BK и DC следует из равнобедренности △ABK. Осталось лишь показать, что уголки ∠BKO и ∠DCO равны. Посмотрите на смежные им уголки и завершите решение!
Так как — биссектриса, то
. В силу параллельности
и
также
.
Пусть — центр окружности, описанной около
. Тогда
, так как
— равнобедренный треугольник. Откуда
.
![]()
Также равнобедренными будут треугольники (
как радиусы) и
(углы
и
равны по
вышесказанному). Значит,
Тогда по двум сторонам и углу между ними, потому что
, радиусы
, а углы
Следовательно, и тогда точки
лежат на одной окружности.
Ошибка.
Попробуйте повторить позже
Пусть длины сторон треугольника являются натуральными числами , и одна из его высот равна сумме двух других. Доказать, что
число
является точным квадратом (натурального числа).
Источники:
Подсказка 1
Нам нужно как-то записать условие на то, что одна высота равна сумме двух других. Через что тогда можно выразить высоту, чтобы равенство не хотелось сразу стереть из-за его громоздкого вида?
Подсказка 2
Верно, через площадь треугольника и сторону. Тогда наше равенство будет выглядеть как 2S/a = 2S/b + 2S/c => 1/a = 1/b + 1/c => bc = ab + ac. Если мы хотим сказать, что сумма квадратов сторон равна точному квадрату, то давайте подумаем какому конкретно квадрату это может быть равно(квадрат, который выражен через a,b,c).
Подсказка 3
Действительно, подходит квадрат (b + c - a)^2, ведь раскрывая скобки, мы получим, что a^2 + b^2 + c^2 + 2bc - 2ab - 2ac = a^2 + b^2 + c^2, так как bc = ab + ac. Что и требовалось доказать.
Пусть — площадь треугольника, а
— высоты к сторонам
соответственно.
Из формулы площади треугольника имеем, что
Без ограничения общности будем считать, что . Тогда
Откуда . Но тогда
и можно сказать, что
Ошибка.
Попробуйте повторить позже
Найти все множества , состоящие из различных натуральных чисел от 1 до 50 такие, что: 1) X содержит не все числа от 1 до 50, но не
меньше трёх из них, 2) X содержит числа 1 и 50, 3) для любых трёх чисел
из X число
также принадлежит
X.
Источники:
Подсказка 1
Попробуйте упорядочить все взятые числа, для фиксированного, подходящего под условия набора и посмотреть на три подряд идущих числа. Что можно сказать?
Подсказка 2
Если у нас есть три подряд идущих числа x, y, z: x < y < z, то число x + z - y, которое больше x, но меньше z, то оно равно y. Что же это значит?
Подсказка 3
Это значит, что y = (x + z)/2, а это критерий арифметической прогрессии. Значит, наш набор - это арифметическая прогрессия. Что мы можем тогда сказать, если она начинается с 1, а заканчивается 50?
Подсказка 4
Это значит, что 49 делится на разность между соседними членами. И либо это 1, либо 7, либо 49. Все варианты нам подходят или нет?
Отсортируем числа из множества по возрастанию:
Для любых трех последовательных чисел число
по условию лежит в
. Но
Тогда это число должно равняться , откуда
. В силу произвольности выбора номера
получаем, что каждое
число является средним арифметическим двух его соседей, но тогда это арифметическая прогрессия.
По условию числа , то есть
, где
- разность прогрессии.
и в силу того, что
, а
натуральное. Имеем единственное решение
.
Ошибка.
Попробуйте повторить позже
Какое максимальное количество простых чисел можно записать, использовав каждую из десяти цифр от 0 до 9 ровно по одному разу?
Источники:
Подсказка 1
Если мы понимаем, что простые числа наши составляют все цифры от 0 до
Подсказка 2
Последней цифрой может быть только 1,2,3,5,7,9. Значит, чисел не больше 6. Попробуйте построить пример на 6, и тогда задача будет решена.
Последними цифрами простых чисел могут быть только . Значит, использовав каждую из десяти цифр от
до
по одному
разу, больше шести простых чисел мы получить не сможем.
6 простых чисел уже может быть:
Ошибка.
Попробуйте повторить позже
На одной стороне каждой из 100 карточек написали одно из натуральных чисел от 1 до 100 включительно (каждое число записано ровно на одной карточке), после чего перевернули их обратными сторонами вверх и разложили в произвольном порядке на столе. За один вопрос Вася может указать на две любые карточки, после чего получает от ведущего ответ, являются ли записанные на них числа соседними (отличающимися на 1). За какое минимальное число вопросов Вася может гарантированно назвать хотя бы одну пару карточек, на которых написаны соседние числа?
Источники:
Подсказка 1
Поймём, что эта задача на оценку + пример! Чтобы придумать пример, подумайте о том, сколько соседей у каждого числа от 1 до 100.
Подсказка 2
Да, у каждого числа от 2 до 99 включительно — два соседа, а у чисел 1 и 100 — один сосед! Тогда можно увидеть алгоритм: задавать вопросы про одну и ту же карточку, постоянно меняю другую карточку. Какой ответ даёт этот алгоритм?
Подсказка 3
Верно, при таких действиях за 98 вопросов мы точно сможем назвать соседние числа! Осталось доказать, что за меньшее число вопросов доказать нельзя. Для этого нужно подумать о задаче в терминах теории графов. Тогда карточки — это вершины, а вопросы — это ребра! Что нужно найти в графе, чтобы доказать, что 98 — искомый ответ на задачу?
Подсказка 4
Да, надо найти Гамильтонов путь (такой путь, в котором каждая вершина встречается ровно один раз) по всем вершинам в графе, в котором ни одно ребро не является ребром, которое появилось вследствие вопроса Васи! Попробуйте посмотреть на задачу при малых n и доказать это утверждение по индукции!
Подсказка 5
База индукция тривиальна, поэтому давайте сразу подумаем о переходе! Такс, а что если посмотреть на вершину из которой выходит ровно одно ребро? А что будет в графе без неё? Можно ли в нём построить нужный нам путь?
Подсказка 6
Да. если есть такая вершина, то задача легко решается по индукции, ведь мы всегда можем переходить от случая с n вершинами к n+1 вершине с помощью добавления одного нужного нам ребра! Но вот незадача: что если нет вершин, из которых ихходит ровно одно ребро?
Подсказка 7
А если нет вершин с степенью 1, то можно точно утверждать, что есть хотя бы две вершины со степенью 0. Остаётся посмотреть на две этих вершин и еще одну вершину степень которой хотя бы 2!
Пример. Пусть Вася выберет какую-то карточку и задаст
вопросов, в каждом из которых он спросит про
и одну из
карточек, отличных от
Общее количество чисел, не соседних с числом, написанным на
не превосходит
если на
написано
или
и
если на
написаны числа от
до
Тогда либо в одном из
ответов будет дан
положительный ответ, и Вася нашёл нужную пару соседних чисел, либо все эти карточки содержат числа, не соседние с числом на
Следовательно, оставшаяся карточка содержит число, соседнее с числом на
Таким образом, Васе достаточно
вопросов.
Оценка. Докажем, что, если Вася задаст всего любых вопросов, он может не найти ни одной пары карточек с соседними числами.
Предположим противное, что задав некоторые
вопросов он смог точно указать на пару карточек с соседними числами. Переведём
задачу на язык теории графов. Карточки будем считать вершинами графа
а заданные Васей вопросы – рёбрами
(синими рёбрами),
соединяющими соответствующие пары карточек. К этим рёбрам нужно добавить ещё одно, соответствующее той паре карточек, на которых
написана пара соседних, по версии Васи, чисел. Теперь нужно доказать, что вершины
могут быть занумерованы в таком порядке, что ни
одно ребро не соединяет две вершины с соседними номерами. То есть, нужно дорисовать в графе путь из
рёбер, проходящий
последовательно по всем
вершинам, и не содержащих ни одного из
«Васиного» синего ребра. Это будет означать, что Васина
догадка не верна. Назовём такой путь красным и будем строить его методом математической индукции по числу вершин графа
Предположим, что в любом графе с числом вершин в котором проведено не больше
синих рёбер, существует красный
путь
по всем вершинам, не содержащий синих рёбер. Построим красный путь в
1) Пусть в есть «крайняя» вершина
из которой выходит ровно одно ребро
В графе
полученном из
удалением
вершины
и ребра
число вершин равно
а рёбер – не больше
выполнено предположение индукции, поэтому
в
можно построить красный путь длины
с началом в вершине
и концом в вершине
Тогда ребро
не
соединяет вершину
с одной из
или
проведя красное ребро из
в эту вершину, получим красный путь длины
в
2) Пусть в нет вершин, из которых выходит ровно одно ребро. В таком случае все синие рёбра инцидентны в сумме
вершинам
степени не меньше
каждая, следовательно, среди них не больше
различных. Следовательно, в
не меньше двух вершин
из
которых не выходит ни одного синего ребра. Удалим из
вершины
и два ребра, выходящие из некоторой четвёртой вершины
(но
не саму вершину). Полученный граф
снова удовлетворяет предположению индукции и в нём можно построить красный путь длины
с началом в вершине
и концом в вершине
Если он не проходит через
или проходит, но не проходит через удалённые рёбра,
соединим
с
и
с
и получим красный путь в
длины 99. В оставшихся случаях, обозначим за
и
вторые концы удалённых
рёбер. Если красный путь в
проходит через
заменим этот фрагмент на
Если он проходит только
через одно удалённое ребро, скажем, через
заменим его на
В обоих случаях получится красный путь в
База индукции - случаи графов с 3 и 4 вершинами - очевидна.
Ошибка.
Попробуйте повторить позже
В возрастающей арифметической прогрессии из натуральных чисел каждый член, кроме последнего, делится на свой номер в прогрессии,
а последний – нет. Докажите, что
является степенью некоторого простого числа.
Источники:
Подсказка 1
Давайте посмотрим на наше условие о том, что все числа с номерами меньше n делятся на свой номер. Эти числа будут вида a+(k-1)d, и если посмотреть по модулю k, то это будет сравнимо с a-d = 0 (mod k). Какое противоречие можно найти, если n (кол-во чисел в прогрессии) - не степень простого?
Подсказка 2
По факту мы поняли что a-d делится на все k<n. А что можно найти у числа, которое не является степенью простого?
Подсказка 3
Делители, которые являются взаимно простыми! Поймите, как это применить, зная что a-d делится на все k<d.
Пусть первый член прогрессии равен а разность равна
Тогда из условия
По условию
ый член последовательности
делится на
(кроме последнего), тогда получим:
Значит, делится на все числа от
до
Пусть
не является степенью простого числа, тогда
где
и
не
имеют общих делителей. Тогда
Значит, так как то
То есть последний член делится на
Противоречие.
Ошибка.
Попробуйте повторить позже
Найти все решения системы уравнений в действительных числах:
Источники:
Подсказка 1
Давайте внимательно посмотрим на нашу систему, что можно сказать о ней? Верно, уравнения в ней циклические! Поэтому можно упорядочить наши переменные, не умаляя общности: x ≥ y ≥ z.
Подсказка 2
Вычтем из первого уравнения третье: x⁵-z⁵ = y³+2z-x³-2y. Заметим, что левая часть уравнения всегда неотрицательна, а правая не больше нуля! Какой вывод можно сделать из этого?
Первое решение.
Если тройка является решением, то решениями являются
. В силу этой цикличности системы мы можем не
умаляя общности считать
Вычтем из первого уравнения третье и получим
Из следует
а из
следует
Таким образом, равенство выше может выполняться только в случае одновременно обращения трёх неравенств в равенства:
При подстановке в любое из уравнений системы получаем
Второе решение.
Заметим, что в любой тройке, являющейся решением, все переменные одного знака: они либо все неотрицательны, либо все
неположительны. Это следует из того, что нечётная степень числа имеет тот же знак, что и само число. Действительно, среди переменных
две имеют одинаковый знак, тогда правая часть уравнения, содержащего эти переменные, имеет тот же знак, значит и левая часть, а с ней и
третья переменная имеют тот же знак. Кроме того, если одна из переменных равна то левая часть соответствующего
уравнения равна
значит сумма двух чисел одного знака в правой части тоже равна
поэтому каждое из этих чисел равно
Внесём эту тройку в ответ. Тогда дальше можно считать, что все переменные не равны При умножении решения системы на
снова получаем решение, следовательно, дальше можно считать, что
а потом внести в ответ тройку с противоположными
знаками.
Сложим все три уравнения и перенесем правую часть в левую:
Теперь рассмотрим функцию Нетрудно понять, что при
значении
функции отрицательно, а при
положительно, а также при
оно равно
Отсюда следует, что все
переменные не могут быть одновременно больше или одновременно меньше
Так как иначе
ведь в
левой части стоит сумма трёх чисел одного знака, поэтому они все должны равняться
откуда следует, что при этом
Итак, остались два случая, и
Если тогда
— это не решение.
Если — это тоже не решение.
Таким образом доказано, что других решений, кроме уже найденных, нет.
Ошибка.
Попробуйте повторить позже
Тройка действительных чисел такова, что
и
Найти значение выражения
Источники:
Подсказка 1
Мы знаем, что в формуле разности косинусов есть произведение синусов и произведение косинусов...А у нас есть условие на суммы синусов и суммы косинусов..Что можно сделать с ними?
Подсказка 2
Возвести в квадрат! В одном выражении будут все попарные произведения синусов, а в другом - косинусов. И тогда остается свернуть эти два выражения в нужное нам)
Возведём в квадрат каждое из двух уравнений:
Сложим эти уравнения, используя Получим:
Ошибка.
Попробуйте повторить позже
В треугольнике биссектрисы углов
и
пересекают стороны
и
в точках
и
соответственно. Известно,
что длина стороны
равна сумме длин отрезков
и
Найдите величину угла
Источники:
Подсказка 1
Раз у нас есть условие на то, что сторона AC равна сумме отрезок, то давайте разобьем нашу сторону как раз на две части, каждая из которых будет равна одному из отрезков в условии) Причем т.к. у нас тут биссектрисы, то удобно будет сделать так, чтобы равные отрезки прилегали к одной вершине. Разделим так нашу сторону точкой D. Что можно заметить на картинке теперь?
Подсказка 2
Пусть биссектрисы пересекаются в точке I. Тогда треугольники API и ADI равны! Тоже можно сказать про ICK и IDC. А дальше остается просто счет уголков)
Первое решение (счетное).
![]()
Давайте будет пользоваться свойством биссектрисы:
Тогда:
Теперь подставим это в
Домножим на знаменатели:
Тогда из теоремы косинусов для треугольника следует, что
Отсюда получаем ответ.
Второе решение (более идейное).
![]()
Отметим точку на отрезке
такую что
Тогда из условия следует, что
Заметим, что треугольники
равны по двум сторонам и углу между ними. Аналогично равны треугольники
Из этого следует:
Теперь воспользуемся тем, что
Тогда по теореме о сумме углов:
Ошибка.
Попробуйте повторить позже
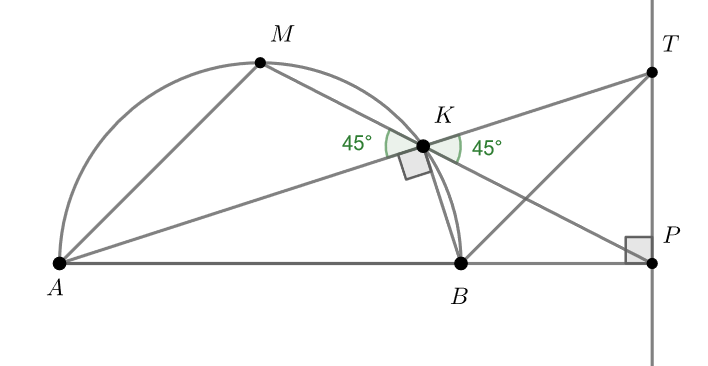
На отрезке , как на диаметре, построен полукруг, в котором точка
середина дуги
. На дуге
выбрана произвольная
точка
, отличная от
и
, через
обозначена точка пересечения прямых
и
. Пусть
— точка пересечения
прямой
и перпендикуляра к прямой
, проведённого через точку
. Докажите, что длины отрезков
и
равны.
Подсказка 1
Первое, что бросается в глаза — большое количество прямых углов на картинке. Прямой ВРТ говорит о том, что для решения задачи достаточно доказать, что угол ТВР, например, равен 45 градусам. Что ещё, связанное со вписанностью и прямыми углами, можно указать на картинке?
Подсказка 2
Хочется показать, что на картинке имеется вписанный четырехугольник, используя один из признаков такого четырехугольника. Также осталось вспомнить, что точка М — середина дуги АВ окружности, это тоже важно для некоторых углов!
Для начала заметим, что так как
— диаметр полуокружности. По условию прямая
— перпендикуляр к
, то
есть
Тогда в четырехугольнике
внутренний угол
равен внешнему углу
при противоположной вершине.
Значит, четырёхугольник
вписанный.
Так как — середина полуокружности,
а опирающийся на эту дугу вписанный угол
как вертикальные углы, а
потому что
— вписанный четырехугольник.
Тогда то есть прямоугольный треугольник
имеет угол в
Значит,
—
равнобедренный и
Ошибка.
Попробуйте повторить позже
Доказать, что для любых действительных чисел из интервала
выполнено неравенство
Источники:
Подсказка 1
Доказать классическое неравенство существует достаточно способов, но при переменных, заданных промежутком, можно отдельно пооценивать разные части выражения.
Подсказка 2
Рассмотрим первую дробь: в ее числителе сумма двух переменных, не превосходящих единицу, следовательно, их сумма не превосходит 2.
Подсказка 3
Перейдем к знаменателю! Здесь тоже сумма! Ваша очередь оценивать!
Подсказка 4
Теперь дробь целиком! Числитель не больше двух, знаменатель - трёх, значит, дробь не превышает 2/3.
Подсказка 5
Аналогичная оценка работает на других слагаемых нашего выражения: если каждое из них не превосходит 2/3, то их сумма не превосходит 2!
По условию, все числа неотрицательны и не превосходят 1 следует, что их попарные суммы не больше 2. Заменим в
знаменателе каждой дроби левой части неравенства 2 на соответствующую сумму, от чего каждый знаменатель не увеличится и неравенство
усилится. Получим:
Ошибка.
Попробуйте повторить позже
Пусть — точка пересечения высот остроугольного треугольника
точка
— середина стороны
На стороне
выбрана
точка
такая, что прямая
делит отрезок
пополам. Доказать, что отрезки
и
перпендикулярны.
Источники:
Подсказка 1
Есть прямая BH, которая делит отрезок пополам...чем-то напоминает медиану в треугольнике, с которой можно выполнить полезное дополнительное построение. Какое?
Подсказка 2
Удвоим отрезок BP, отметив новую точку T, после чего у нас появится параллелограмм. Теперь мы можем посчитать в нем уголки. Вернемся к условию. Чем являются MN и KP для треугольников на рисунке? На чертеже много прямых и равных углов, быть может, стоит попробовать найти подобие?
Подсказка 3
Заметим, что MH и CP это медианы треугольников BCT и AHC, в которых есть перпендикулярные стороны. Что же осталось доказать?)
![]()
Обозначим точку пересечения отрезков и
за
Отметим на луче
точку
такую, что
является серединой отрезка
Диагонали и
четырёхугольника
делятся точкой пересечения
пополам, поэтому он является параллелограммом,
его стороны
и
параллельны и
то есть
а
В треугольнике
следовательно, треугольники
и
подобны. Их
соответствующие стороны
и
перпендикулярны, а отрезки
и
являются медианами этих треугольников, проведёнными к
соответствующим сторонам, поэтому тоже перпендикулярны.
Ошибка.
Попробуйте повторить позже
Перестановка чисел в некотором порядке называется забавной, если в ней каждое число, начиная со второго слева, либо
больше всех чисел, стоящих левее него, либо меньше всех чисел, стоящих левее него. Например, перестановка
является забавной, а перестановка
— нет. Найти количество всех различных забавных перестановок чисел
Источники:
Подсказка 1
Если собирать последовательности с первого элемента, то будет трудно...но можно пойти с конца! Сколько есть вариантов для последней позиции?
Подсказка 2
Всего 2!(какие?). Теперь мы можем выбирать предпоследнюю цифру, но ведь она связана с последней? Какие тогда комбинации последних двух цифр могут быть?
Подсказка 3
(n-1, n), (1, n), (2, 1), (n, 1). Интересно, было 2 варианта, стало 4...попробуем обобщить наши рассуждения. Подумаем, как выглядят первые k чисел при любом k от 1 до n.
Пойдём с конца. Последнее число забавной перестановки либо больше, либо меньше всех чисел множества
следовательно,
оно равно 1 или
Предпоследнее число
забавной перестановки либо больше, либо меньше всех чисел множества
кроме
то есть это наименьший или наибольший элемент во множестве
или во множестве
В каждом из
случаев есть ровно две возможности выбора, варианты для двух последних чисел перестановки выглядят так
Несложно убедиться, что при любом
первые
чисел
перестановки образуют интервал из
подряд
идущих чисел из множества
а число
является в этом интервале минимальным или максимальным — всего две
возможности, кроме самого первого числа
для которого остаётся единственная возможность. Всего получаем ровно
возможностей выбора.
Ошибка.
Попробуйте повторить позже
Найти все решения в действительных числах системы уравнений
Источники:
Подсказка 1
В уравнениях степени небольшие, поэтому не составит труда немного поработать ручками и с помощью простых преобразований прийти к чему-то более красивому. Быть может, стоит попробовать выразить все переменные через одну из них?
Подсказка 2
Вычтем первое уравнение из двух других, теперь мы знаем, как выразить все переменные через одну! Теперь можно подставить их в любое уравнение и что-то понять.
Подсказка 3
Получится кубическое уравнение, у которого можно угадать корень. Остается лишь найти остальные или доказать, что их нет!
Вычтем первое уравнение из второго и третьего, получим:
Подставим выражения в первое уравнение, получим
Одним из его корней является поэтому
Дискриминант второй скобки отрицателен, поэтому единственным действительным корнем кубического уравнения и решением исходной
системы является Тогда
Ошибка.
Попробуйте повторить позже
Десятичная запись натурального числа содержит каждую цифру от 0 до 9 ровно один раз. Обозначим через
сумму пяти двузначных
чисел, составленных из первой и второй, третьей и четвёртой
девятой и десятой цифр
, а через
— сумму четырёх двузначных
чисел, составленных из второй и третьей, четвёртой и пятой
восьмой и девятой цифр
Оказалось, что
равно
может ли
начинаться с чётной цифры?
Источники:
Подсказка 1
Распишем условие с помощью десятичной записи чисел. Какое уравнение на числа A и B у нас получится и что из него будет следовать?
Подсказка 2
Понимаем, что сумма первой и последней цифры числа делится на 9! Какой тогда может быть их сумма? Как найти связь между цифрами на четных позициях и на нечетных?
Подсказка 3
Подставляем в наше уравнение из подсказки 1 сумму первой и последней цифры, которая равна 9(почему?). Теперь мы можем найти связь между суммами цифр на четных позициях и на нечетных, а также мы знаем сумму всех цифр. Остаётся лишь осознать, как это применить)
Пусть где
— некоторая перестановка чисел
Тогда
Если то
Отсюда следует, что делится на 9.
Одна из двух различных цифр ненулевая, поэтому
Значит,
Вспомним, что — некоторая перестановка чисел
поэтому сумма всех цифр
равна
— нечётна. Тогда
Следовательно, цифра чётна, а цифра
— нечётная цифра.
Ошибка.
Попробуйте повторить позже
На некотором острове живёт человек, каждый из которых является либо рыцарем, который всегда говорит правду, либо лжецом,
который всегда лжёт.
Однажды все жители этого острова выстроились в ряд, и первый из них сказал:
Затем второй сказал:
и так далее до сотого, который сказал:
Определите, сколько рыцарей может проживать на этом острове. Найдите все ответы и докажите, что других нет.
Источники:
Подсказка 1
Что можно сказать про человека, который был первым рыцарем? Чему равно число рыцарей, если мы знаем номер первого из них?
Подсказка 2
Число рыцарей равно номеру первого рыцаря, поскольку, если он первый, значит все до этого соврали, а это значит, что кол-во рыцарей не делится ни на какие числа от 1 до х, где х - номер первого рыцаря. Что тогда это дает? На каких позициях стоят другие рыцари?
Подсказка 3
Рыцари стоят на позициях х,2х,3х,….,х^2. Ведь рыцарей ровно х, и при этом все люди, которые стоят на местах х,2х,…,х^2 не соврали. Теперь мы знаем, где стоят рыцари. А какие условия это накладывает на х? Что , в силу этих условий, можно сказать про их кол-во?
Подсказка 4
В силу этих условий, получаются две оценки: х^2<=100, x(x+1)>100. Откуда х=10. Но нет ли в наших рассуждениях какой-то ошибки, за которую могут снять 1-2 балла? Вспомните рассуждения и найдите ее.
Подсказка 5
Верно, в наших рассуждениях, мы сначала брали первого рыцаря, а потом что-то из этого находили. Но мы не задумались, что первого рыцаря может и не быть! А ведь такая ситуация тоже подходит.
Если рыцарей нет, то все говорящие врут, так как не является делителем какого-либо натурального числа.
Если рыцари есть, то пусть первый рыцарь имеет номер Тогда число рыцарей является делителем числа
но не будет являться
делителем чисел
поскольку до него все лгали. Легко видеть, что тогда число рыцарей равно
Тогда ему кратны только
числа
Здесь
Ровно на этих позициях и только на них и должны стоять рыцари, откуда всего их
будет
Имеем
Под это условие подходит только
В качестве примера достаточно поставить рыцарей
на позиции
и
Ошибка.
Попробуйте повторить позже
В некоторых клетках прямоугольной доски размера на
сидят по одной черепашке. Каждую минуту каждая из них одновременно
переползает в одну из клеток доски, соседнюю с той, в которой они находятся, по стороне. При этом, каждый следующий ход
делается ими в направлении, перпендикулярном предыдущему: если предыдущий ход был горизонтальным — налево или
направо, то следующий будет вертикальным — вверх или вниз, и наоборот. Какое максимальное количество черепашек может
перемещаться по доске неограниченное время так, что в каждый момент в каждой клетке будет находиться не более одной
черепашки?
Сначала покажем, что черепашек могут так перемещаться. Выделим в верхнем левом углу прямоугольник
Поставим в
каждую его клетку по черепашке. Разобьем его на квадратики
И пусть в каждом квадратике черепашки перемещаются по циклу
против часовой стрелки. Тогда все черепашки всегда смогут сделать ход.
Докажем, что большего количества черепашек быть не может. Раскрасим нашу доску в цвета в горошек (в первой строке чередуются
цвета
и
во второй —
и
в третьей — снова
и
и так далее). Заметим, что клеточек цвета
ровно
Рассмотрим клеточки второго цвета. Заметим, что все черепашки на клеточках второго цвета через
хода попадут в клеточки четвертого
цвета. Тогда в данный момент черепашек на клеточках второго цвета не больше, чем черепашек на клеточках четвертого цвета, то есть
также не больше, чем
Нам осталось оценить сверху количество черепашек, стоящих в данный момент на клеточках первого и
третьего цвета. Чтобы это сделать, достаточно подождать один ход, тогда все эти черепашки попадут на клеточки второго и
четвертого цвета. А затем проделать те же самые рассуждения. То есть всего черепашек действительно не больше, чем
Ошибка.
Попробуйте повторить позже
Найти все натуральные , которые можно представить в виде суммы
где — минимальный делитель
, отличный от
и
— какой-то делитель
Подсказка 1
По условию a- минимальный делитель n, отличный от 1. В связи с этим хочется попытаться узнать его наверняка. Может даже получится доказать, что он равен 2. Давайте предположим противное. Какое противоречие мы получим?
Подсказка 2
Если минимальный делитель отличен от 2, то n- нечетное число и все его делители также нечетны. Но тогда сумма a²+b² не может быть нечетной. Противоречие. Мы выполнили свою цель и перешли к новой задаче: n=4+b². Какое ограничение возникает на b?
Подсказка 3
Заметим, что n и b² делятся на b, значит 4 также делится на b. Такое бывает крайне редко, поэтому довести решение до конца вам не составит никого труда!
Если нечётно, то и все его делители нечётны, поэтому правая часть равенства
чётна — противоречие. Следовательно,
чётно и его минимальный неединичный делитель
равен
а
По условию делит
значит, делит и разность
поэтому
должно быть равно одному из чисел
При
этом
равно
соответственно. Первый случай не подходит ввиду нечётности, остальные два удовлетворяют условию
задачи.
Ошибка.
Попробуйте повторить позже
Определим последовательность следующим образом: пусть
произвольное положительное число, меньшее 1 , и
для всех
Докажите, что
Источники:
Докажем сначала, что Для этого воспользуемся индукцией по
База индукции
верна по условию. Шаг индукции: при
выполнены неравенства
поэтому
и
то есть
Ввиду доказанного, для всех
поэтому
что и требовалось доказать.



