Пусть путник находится в точке Множество прямых, удалённых от него на 1 км, это множество касательных к окружности, описанной вокруг путника с центром в точке и радиусом 1 км. Опишем около неё правильный шестиугольник Докажем, что ломаная удовлетворяет условию задачи, так что путник может идти по такому маршруту.

Действительно, если радиус вписанной окружности равен 1, то сторона правильного шестиугольника равна . А длина ломаной по намеченному пути равна

Ломаная пересекает каждую касательную окружности : — крайними точками, остальные — внутренними. Поэтому путник на таком маршруте гарантированно вышел из леса, пройдя не больше заданного в условии расстояния.

Покажем, что система

является подходящей. Обозначим систему неравенств за . Покажем, что любая пара целых чисел, удовлетворяющих является решением.

Действительно, пусть верно, тогда каждое из подкоренных выражений числителей неотрицательно, а каждый из числителей обращается в ноль, поскольку числа целые.

Теперь покажем, что никакая из других пар не является решением. Пусть — решение, тогда следовательно, — целое и , следовательно, — целое. Кроме этого, , а значит, , откуда верно первое неравенство системы Аналогично получаем, что верно второе неравенство системы

Сгруппируем крайние члены

По формуле суммы тангенсов

Заменим синус от 45 градусов на равный ему косинус и воспользуемся формулой произведения косинусов

Осталось заметить, что функция убывает на отрезке , а значит, верны неравенства для всех , следовательно, верны неравенства для всех , т.е. каждое слагаемое в сумме меньше 1. Таким образом, вся сумма меньше 22.

Рассмотрим второе уравнение системы

Заметим, что не является решением, тогда

Поставим в первое уравнение системы и преобразуем, получив уравнение 4-ой степени относительно

Заметим, что раз — решения системы, то будут корнями данного уравнения, причём различными, иначе бы какие-то решения системы совпали в силу выражения через Т.к. многочлен 4-ой степени может иметь не более 4 корней, значит, других не будет. Тогда по теореме Виета

Теперь возьмём второе уравнение системы, удвоим его и сложим с первым уравнением, получим

Заметим, что не является решением, тогда

Подставим в первое уравнение системы и преобразуем, получив уравнение 4-ой степени теперь относительно

Аналогично случаю с по теореме Виета

В итоге

Докажем, что для всех верно неравенство

______________________________________________________________________________________________________________________________________________________

Для этого достаточно показать, что Действительно, пусть , тогда , следовательно, выпукла вверх на отрезке Кроме этого и , а значит, для всех , а значит, для всех , откуда получаем требуемое.

_________________________________________________________________________________________________________________________________________________________________________________

Так как и то применяем доказанное неравенство:

Вычислим

То есть нужно найти остаток по модулю Рассмотрим первое слагаемое.

Раскрывая скобки, как минимум два раза выберется из скобок, что дает в сравнении по модулю Это верно, кроме случаев, когда были выбраны все единицы или когда было выбрано одно из всех скобок. Тогда, используя бином Ньютона, получаем, что первое слагаемое сравнимо с

Аналогично получаем, что второе слагаемое сравнимо с

Тогда получаем

Следовательно, остаток равен

Поскольку произведение первых 6 натуральных чисел равно то искомое число не больше

Осталось доказать, что произведение любых подряд идущих 6 натуральных чисел делится на . Поделим:

и получим натуральное число способов выбрать шестёрку из элементов. Действительно, делится.

В задаче речь идет о трехгранном угле с вершиной в центре сферы, высекающем на сфере криволинейный треугольник. Площадь этого треугольника требуется выразить через радиус сферы и данные в условии плоские углы трехгранного угла, которые будем обозначать

Рассмотрим сначала две различные плоскости, проходящие через центр сферы. Пусть угол между этими плоскостями равен Плоскости пересекают сферу по большим окружностям. Касательные к окружностям в их точке пересечения также образуют угол Площадь поверхности сферы равна Площадь высекаемой плоскостями «дольки» (указанной на рисунке цветом) очевидно пропорциональна величине и равна

Три плоскости (содержащие грани трехгранного угла) разбивают сферу на треугольников. Искомую площадь криволинейного треугольника обозначим через а его углы (которые, очевидно, являются двугранными углами трехгранного угла за Площади криволинейных треугольников, примыкающих к сторонам треугольника обозначим С каждым из этих треугольников образует «дольку», поэтому Оставшиеся из -х нерассмотренных криволинейных треугольников симметричны -м рассмотренным относительно центра сферы. Значит, суммарная площадь рассматриваемых четырех треугольников равна половине площади сферы, то есть Тогда сложим первые три уравнения и воспользуемся четвертым:

Из теоремы косинусов для трехгранного угла

Отсюда получаем ответ.

Первое решение.

Заметим, что Далее проверкой до целой части от соответствующего арифметического корня проверяем оба множителя на простоту. Разложение получено.

Второе решение.

Заметим, что Тогда

Следовательно, пары чисел или имеют общие делители, отличные от 1. Найдём наибольший общий делитель чисел по алгоритму Евклида:

Следовательно, – простое число. Остаётся разделить на

Первое решение.

Заметим, что за каждый неудачный выстрел стрелок просто теряет один патрон, а за каждый удачный выстрел получает патронов на один больше, чем очков, но при этом теряет один патрон за этот выстрел. Получается, что очков суммарно получено столько же, сколько получено дополнительных патронов.

Так как стрелок промахнулся 2023 раза, то он получил дополнительных патрона. Столько он получил и очков.

Второе решение.

Пусть числа выстрелов, результатом которых было получение и очков соответственно. Тогда общее число выстрелов равно:

Каждый выстрел приносит такие очки: При этом с каждым результатом связано определённое число выстрелов, а именно:

1.

Если был промах, то этот результат не даёт дополнительных выстрелов, и с ним связан единственный выстрел, который и дал промах.

2.

Если было получено одно очко, то с этим результатом связано выстрела, а именно, тот, который дал этот результат, и плюс два дополнительных премиальных.

3.

Если было получено очка, то с этим результатом связано выстрела: один — который дал результат, и премиальных.

4.

Если было получено очка, то с этим результатом связано выстрелов (аналогичные рассуждения: один исходный премиальных).

Тогда рассмотрим сумму:

Заметим, что в этой сумме каждый выстрел учтен ровно два раза, тогда:

Заметим, что это выражение - количество набранных Юрой очков.

Предположим, что существуют.

Обозначим

Тогда из условия получаем

Если обе функции являются константами, то левая часть равенства является константой, а в правой можно получать разные значения при разных

Тогда хотя бы одна из функций не равна тождественно константе, пусть это То есть существуют такие что

Подставляем в уравнение:

Получаем

При имеем

При имеем

Получается, что

Противоречие с тем, что

Следовательно, таких функций не существует.

Заметим, что площадь прямоугольника равна сумме площадей прямоугольников разбиения. Так как у каждого маленького прямоугольника длины сторон выражаются целыми числами, при этом длина хотя бы одной его стороны чётна, то эта площадь четна. Тогда длина хотя бы одной стороны исходного прямоугольника также является чётным числом (иначе площадь была бы нечетной).

а) Так как число не рациональное число, то оно не может быть корнем многочлена степени с целыми коэффициентами, значит его степень хотя бы Многочлен удовлетворяет условию задачи.

б) Заметим, что остаток при делении на равен Тогда для некоторого многочлена Тогда

Предположим, что Преобразуем уравнение:

Тогда, так как то число целое и не кратно трем. Значит, тоже целое, но число не может быть степенью тройки (нулевой быть не может, так как оно больше а ненулевой - так как оно не кратно Таким образом, В силу симметрии относительно перестановки получим, что Пусть Тогда:

Домножим на

Пусть Если то Значит, тогда Получим что, или Откуда получим ответ.

Разделим обе части уравнения на

Отсюда получаем, что или Поскольку число не является целым, остается найти количество целых значений таких, что

Решениями неравенства являются целые числа

Пусть пара натуральных чисел удовлетворяет исходному уравнению

(1)

Тогда

1.

Положив и подставив в получим

Очевидно, что . Поэтому . Без ограничения общности можно считать, что в этой паре . Будем это записывать как

2.

По условию, число является корнем многочлена

(2)

По теореме Виета, этот многочлен еще имеет корень причем

Отсюда следует, что и Поэтому уравнение имеет еще одно решение в натуральных числах

Это означает, что для многочлена справедливы равенства

Заметим, что

Поэтому число лежит между корнями многочлена а именно:

Следовательно,

Итак, для любого решения существует другое решение, у которого максимальный элемент окажется меньше. Таким образом, мы можем строить новые решения, у которых максимальный элемент становится все меньше. Но при этом этот максимальный элемент, постоянно уменьшаясь, остается натуральным числом, что невозможно. Пришли к противоречию. Значит, исходное уравнение решений в натуральных числах не имеет.

Рассмотрим числа вида , где — нечётное. Так как чисел указанного вида бесконечно много, то среди них найдутся два числа и имеющие одинаковые остатки от деления на Тогда разность делится нацело на При этом и число является чётным. Так как и числа и взаимно просты, то число делится нацело на а следовательно, и на

Используем формулу косинуса тройного угла получаем

Разложим нашу левую часть в произведение чисел, каждое из которых по модулю не больше 1.

По основному тригонометрическому тождеству получаем

По формуле синуса двойного угла получаем

По формуле косинуса двойного угла получаем

Так как и то равенство возможно только в двух случаях

Рассмотрим систему

Решим уравнение Получаем Заметим, что эти решения также являются и решениями второго уравнения системы, поэтому для первой системы имеем

Рассмотрим теперь вторую систему

Решим уравнение Получаем Подставим эти решения во второе уравнение системы и получим — противоречие. Значит, у второй системы нет решений.

Искомое число наборов посчитаем, суммируя количество наборов с заданным числом ненулевых групп:

• При такой набор единственный;
• При их
• При уже
• 
• При в итоге

Определим многочлены

Как известно из правила раскрытия скобок, такая сумма всевозможных многочленов это сумма по всем наборам и она равна

Если мы сложим эту сумму с суммой таких же многочленов от отрицательных аргументов, то многочлены с нечётными индексами взаимноуничтожатся:

Используем полученные результаты:

что и требовалось:

Рассмотрим треугольник с выбранной внутри него точкой так, что

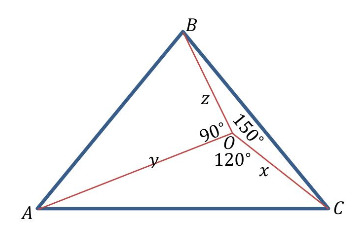
Условия системы представляют собой теорему косинусов (в т.ч. теорему Пифагора) для треугольников

Отсюда нетрудно понять, что Теперь заметим, что

Площадь треугольника найдем по формуле Герона:

Следовательно,