Ошибка.
Попробуйте повторить позже
Середины всех высот некоторого тетраэдра лежат на его вписанной сфере. Верно ли, что тетраэдр правильный?
Источники:
Подсказка 1
Попробуем разобраться в этом тетраэдре. Мы знаем, что середина каждой высоты лежит на вписанной сфере. Какое неравенство, связанное с высотой и радиусом вписанной сферы, мы можем получить?
Подсказка 2
Если Hi- длина произвольной высоты тетраэдра, то Hi/2<=2r, где r- радиус вписанной сферы. Это можно увидеть, если провести плоскость, параллельную плоскости основания высоты и касающуюся вписанной сферы. Что же может дать нам это неравенство? Полезно было бы вспомнить о том, что Hi и r связаны объёмом тетраэдра...
Подсказка 3
Обозначим за Si- площадь произвольной боковой грани. Тогда: 3*V=Hi*Si=r*(S1+S2+S3+S4), где V- объем тетраэдра. Попробуйте теперь воспользоваться неравенством Hi/2<=2r...
Подсказка 4
Подставив неравенство в равенство, мы получим, что: r*(S1+S2+S3+S4)<=4*r*Si. Сократим обе части на 4*r: (S1+S2+S3+S4)/4<=Si. Получается, что произвольно выбранная площадь не меньше среднего арифметического всех площадей. Это как-то странно...
Подсказка 5
Давайте предположим, что Si не больше всех оставшихся площадей. Тогда: Si=(Si+Si+Si+Si)/4<=(S1+S2+S3+S4)/4<=Si. Это означает, что все Si равны между собой. Тогда и все высоты равны между собой. Во что превращается неравенство Hi/2<=2r?
Подсказка 6
Положим, что S1=S2=S3=S4=S, а H1=H2=H3=H4=H. Т.к. H*S=r*(S1+S2+S3+S4) получаем, что H=4r. Но тогда высоты обязаны содержать центр вписанной окружности и точку касания с гранью. Может как-то выразить длины ребер через высоты...
Подсказка 7
Для определенности проведем высоту AH и будем искать ребро AB. По теореме о касательной и секущей получаю, что BH^2=H*H/2. Теперь осталось воспользоваться теоремой Пифагора для треугольника ABH и увидеть, как AB выражается через H.
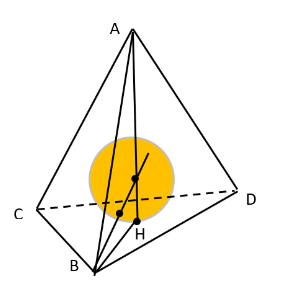
Рассмотрим тетраэдр удовлетворяющий условию задачи. Заметим, что по условию для любой высоты
данного тетраэдра
справедливо неравенство
где
— радиус вписанной сферы, то есть
Пусть — площадь грани, на которую опущена высота
Докажем, что
Предположим противное. Выберем
грань минимальной площади (если таких граней несколько, то берём любую из них). Без нарушения общности можно считать, что её
площадь равна
(иначе можно ввести переобозначения). Так как не все
равны между собой и
- наименьшая из них,
то
Выразим объём тетраэдра двумя способами:
Отсюда что противоречит неравенству
Итак, все равны, поэтому все
равны, так как
Обозначим за
длину этих равных высот. Из приведённого выше
соотношения для объёма получаем
то есть неравенство обращается в равенство. Но это возможно только в случае, если высота
содержит центр сферы и точку касания с гранью (и так для каждой высоты).
Пусть - основание высоты тетраэдра, опущенной из точки
Тогда
совпадает с точкой касания сферы и грани
Пусть
тогда по теореме о касательной и секущей
По теореме Пифагора из прямоугольного треугольника
получаем
Аналогично получаем такое же выражение для остальных рёбер тетраэдра, следовательно, они равны между собой, то есть тетраэдр правильный.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное обучение
в Школково
Для детей ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Брянской областей, а также школьникам, находящимся в пунктах временного размещения Крыма обучение на платформе бесплатное.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ или олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




