Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде известно, что
Через точки
и
параллельно
проведена
плоскость, пересекающая ребро
в точке
а) Докажите, что — середина
б) Найдите расстояние от точки до плоскости сечения.
Источники:
а) Назовем плоскость, проходящую через и
параллельно
плоскостью
Рассмотрим плоскость
Эта плоскость содержит
и пересекает
в середине — точке
Сечение параллелепипеда этой плоскостью —
прямоугольник
Проведем через точку
прямую
Тогда
Следовательно,
— сечение параллелепипеда плоскостью
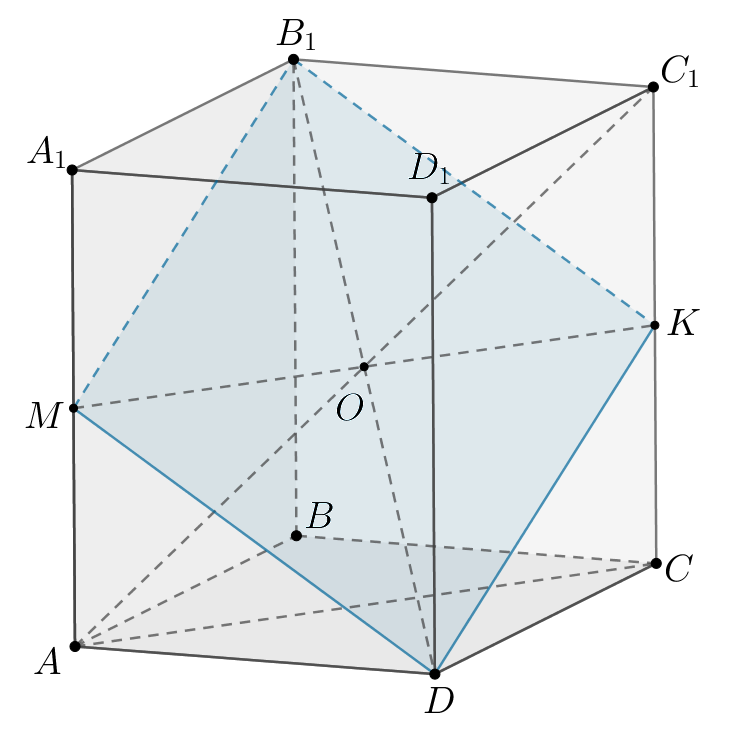
Так как — середина
то
— точка пересечения диагоналей
параллелепипеда, следовательно,
— середина диагонали
Значит, по
теореме Фалеса для
где
имеем:
— середина
Что и
требовалось доказать.
б) Рассмотрим многогранник Его объем равен половине объема
параллелепипеда:
Если из этого объема вычесть объемы
пирамид
и
каждый из которых равен
то
получим объем пирамиды
С другой стороны, если — расстояние от точки
до плоскости
то объем пирамиды
равен
Следовательно
Из этого равенства можно найти если найти площадь сечения.
По теореме Пифагора
Пусть Тогда по теореме косинусов из
Тогда Так как
— параллелограмм (плоскость
пересекает параллельные грани параллелепипеда по параллельным прямым), то
получаем
Следовательно,
б)
Ошибка.
Попробуйте повторить позже
В основании прямой призмы лежит параллелограмм
На ребрах
и
взяты точки
и
соответственно.
Причем
а
— равнобедренная трапеция с основаниями
2 и 3.
а) Докажите, что — середина
б) Найдите площадь трапеции если объем призмы равен 12, а ее
высота равна 2.
Источники:
а) Пусть — проекция точки
на плоскость верхнего основания. Тогда
как прямоугольные по катету и гипотенузе:
Следовательно,
Пусть также
тогда
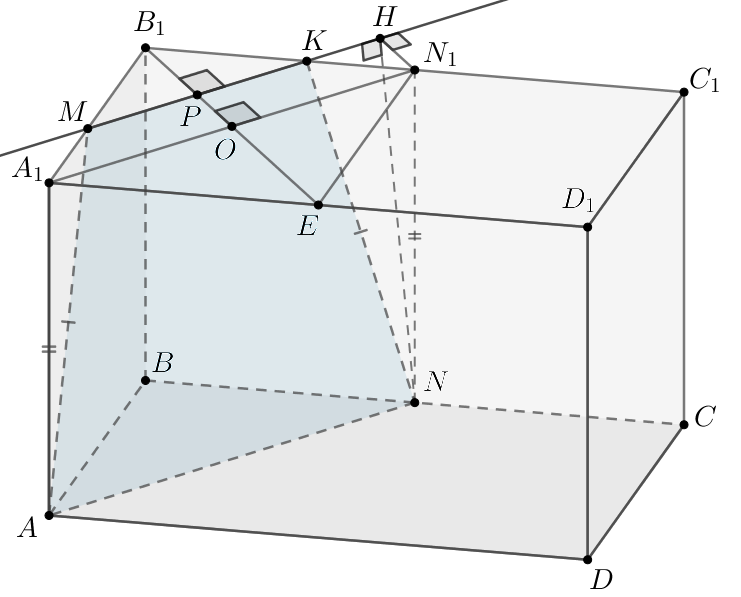
следовательно,
Тогда
Следовательно,
Так как и
то
откуда
— середина
Что и требовалось доказать.
б) Чтобы найти площадь трапеции учитывая, что ее основания
известны, нужно найти ее высоту. Проведем
Тогда по теореме
о трех перпендикулярах
Следовательно,
— искомая
высота.
По условию
следовательно,

По теореме Фалеса, так как и
то
Следовательно,
Значит,
отсекает от параллелограмма
равнобедренный треугольник, следовательно,
— биссектриса
угла параллелограмма. Тогда если
то четырехугольник
— ромб. Значит,
как его диагонали. Площадь ромба
в два раза меньше площади параллелограмма
следовательно,
Тогда по формуле площади ромба
имеем:
Тогда По теореме Фалеса
значит,
Так как отрезки параллельных прямых, заключенные между
параллельными прямыми, равны, то
Следовательно, по теореме
Пифагора из
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании прямой призмы лежит равнобедренная
трапеция
с основаниями
и
Точка
делит ребро
в отношении
а точка
— середина ребра
а) Докажите, что плоскость параллельна прямой
б) Найдите тангенс угла между плоскостью и плоскостью основания
призмы, если
Источники:
а) Так как и
то грани
и
параллельны. Следовательно, плоскость
пересечет их по параллельным
прямым. Значит, плоскость
пересечет грань
по прямой
где
— точка на ребре
Продлим
до пересечения с
прямой
в точке
Тогда точка
являющаяся точкой пересечения
и
является одной из вершин сечения призмы плоскостью
Следовательно,
— сечение призмы плоскостью
Так как то достаточно доказать, что
Из условия следует, что Пусть также
Углы
и
равны как углы между попарно параллельными прямыми.
Следовательно, по катету и острому углу равны
и
так как
Следовательно,
Значит,
— середина ребра

следовательно,
откуда
следовательно,
значит,
можно обозначить
По обратной теореме Фалеса, так как то
Следовательно,
откуда
Что и
требовалось доказать.
б) Так как и
то
—
параллелограмм. Следовательно,
Следовательно,
— равнобедренный с углом
значит, он равносторонний и
Следовательно,
По теореме Пифагора
Так как
и
то
— прямоугольник,
следовательно,
и
прямоугольный с
Также
По теореме Пифагора
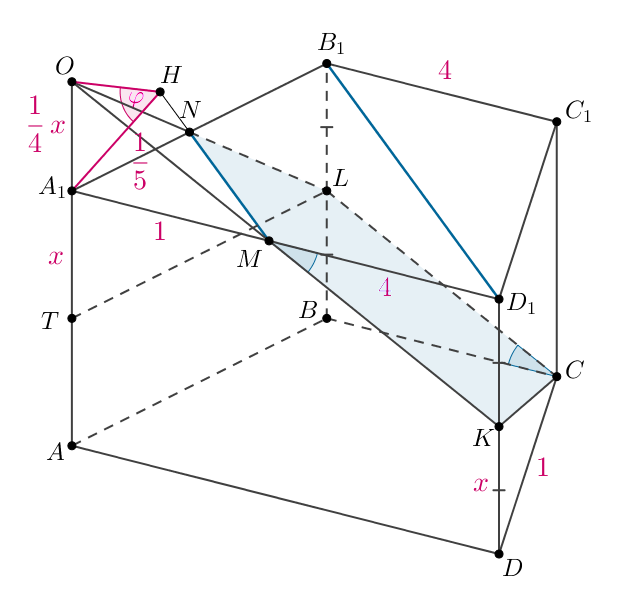
Проведем Следовательно, треугольник
прямоугольный и по
теореме Пифагора
Тогда по теореме Пифагора для получаем
Так как — линия пересечения плоскостей
и
то
проведем
Тогда по теореме о трех перпендикулярах
Следовательно,
— угол между
и
Его тангенс
равен
Следовательно, нужно найти
Заметим, что так как равносторонний и
то
следовательно,
лежит на продолжении отрезка
за точку
Рассмотрим По теореме косинусов
Тогда по теореме синусов из этого же треугольника
Из прямоугольного имеем
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании прямой призмы лежит равнобедренная
трапеция
с основаниями
и
Точка
делит ребро
в отношении
а точка
— середина ребра
а) Докажите, что плоскость параллельна прямой
б) Найдите тангенс угла между плоскостью и плоскостью основания
призмы, если
Источники:
а) Так как и
то грани
и
параллельны. Следовательно, плоскость
пересечет их по параллельным
прямым. Значит, плоскость
пересечет грань
по прямой
где
— точка на ребре
Продлим
до пересечения с
прямой
в точке
Тогда точка
являющаяся точкой пересечения
и
является одной из вершин сечения призмы плоскостью
Следовательно,
— сечение призмы плоскостью
Так как то достаточно доказать, что
Из условия следует, что Пусть также
Углы
и
равны как углы между попарно параллельными прямыми.
Следовательно, по катету и острому углу равны
и
так как
Следовательно,
Значит,
— середина ребра

следовательно,
откуда
следовательно,
значит,
можно обозначить
По обратной теореме Фалеса, так как то
Следовательно,
откуда
Что и
требовалось доказать.
б) Так как и
то
—
параллелограмм. Следовательно,
Следовательно,
— равнобедренный с углом
значит, он равносторонний и
Следовательно,
По теореме Пифагора
Так как
и
то
— прямоугольник,
следовательно,
и
прямоугольный с
Также
По теореме Пифагора
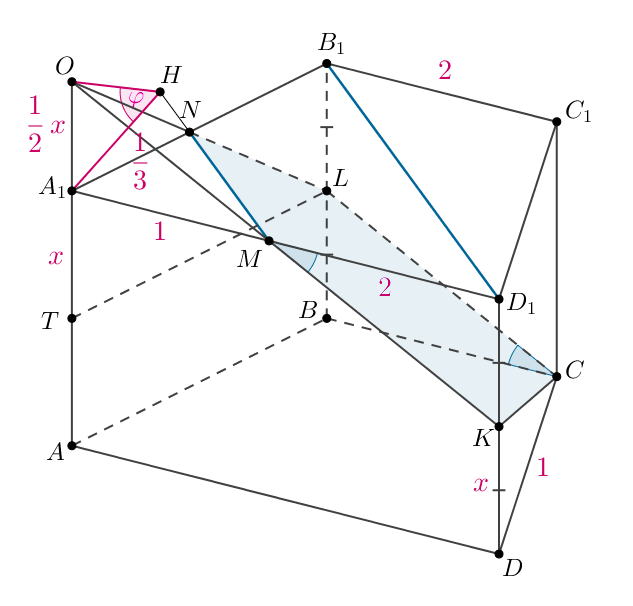
Проведем Следовательно, треугольник
прямоугольный и по
теореме Пифагора
Тогда по теореме Пифагора для получаем
Так как — линия пересечения плоскостей
и
то
проведем
Тогда по теореме о трех перпендикулярах
Следовательно,
— угол между
и
Его тангенс
равен
Следовательно, нужно найти
Заметим, что так как равносторонний и
то
следовательно,
лежит на продолжении отрезка
за точку
Рассмотрим По теореме косинусов
Тогда по теореме синусов из этого же треугольника
Из прямоугольного имеем
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании прямой призмы лежит равнобедренный
треугольник
с основанием
Точка
делит ребро
в
отношении
а точка
— середина ребра
Через
середину
ребра
провели плоскость
перпендикулярную отрезку
а) Докажите, что плоскость параллельна ребру
б) Найдите отношение, в котором плоскость делит отрезок
считая от
точки
если известно, что
Источники:
а) Проведем Так как
— равнобедренный с основанием
то
— середина
Так как
то
Тогда
следовательно,
Следовательно,
— середина
Проведем Тогда
— середина
Следовательно, так как
то по обратной теореме Фалеса
Следовательно,
Так как то
перпендикулярна любой прямой, лежащей в
Заметим, что
— средняя линия в
параллельная
Следовательно,
Тогда по теореме о трех перпендикулярах наклонная
Следовательно,
А так как
то по признаку
Что и требовалось доказать.
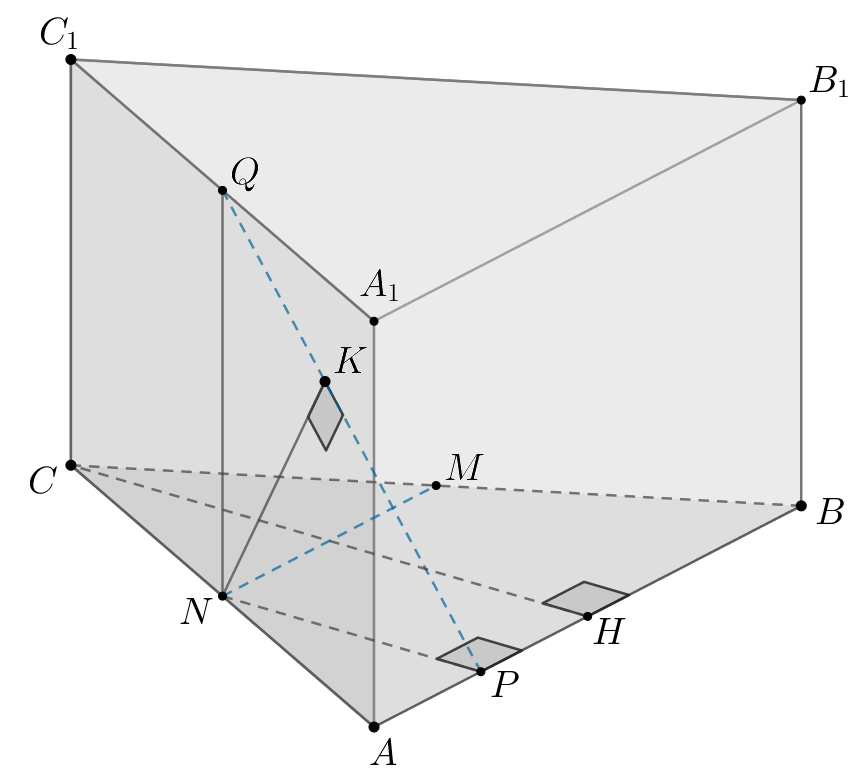
б) Так как то
Следовательно,
по теореме Пифагора из
Проведем Тогда
Следовательно,
— точка, в которой
пересекает
Нужно найти
По свойству прямоугольного
треугольника высота, опущенная из вершины прямого угла, делит гипотенузу на
отрезки, пропорциональные квадратам катетов:
б) 3:1
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании прямой призмы лежит параллелограмм
На ребрах
и
взяты точки
и
соответственно.
Причем
а
— равнобедренная трапеция с основаниями
4 и 6.
а) Докажите, что — середина
б) Найдите площадь трапеции если объем призмы равен 72, а ее
высота равна 2.
Источники:
а) Пусть — проекция точки
на плоскость верхнего основания. Тогда
как прямоугольные по катету и гипотенузе:
Следовательно,
Пусть также
тогда
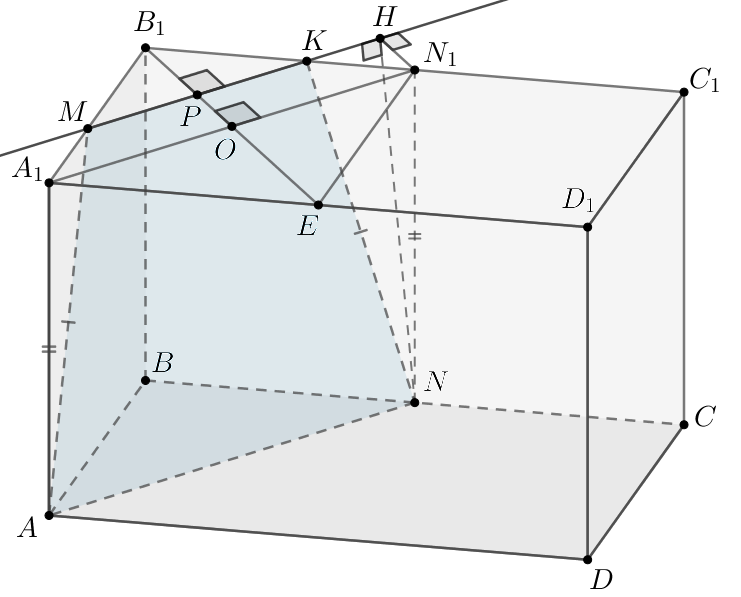
следовательно,
Тогда
Следовательно,
Так как и
то
откуда
— середина
Что и требовалось доказать.
б) Чтобы найти площадь трапеции учитывая, что ее основания
известны, нужно найти ее высоту. Проведем
Тогда по теореме
о трех перпендикулярах
Следовательно,
— искомая
высота.
По условию
следовательно,

По теореме Фалеса, так как и
то
Следовательно,
Значит,
отсекает от параллелограмма
равнобедренный треугольник, следовательно,
— биссектриса
угла параллелограмма. Тогда если
то четырехугольник
— ромб. Значит,
как его диагонали. Площадь ромба
в два раза меньше площади параллелограмма
следовательно,
Тогда по формуле площади ромба
имеем:
Тогда По теореме Фалеса
значит,
Так как отрезки параллельных прямых, заключенные между
параллельными прямыми, равны, то
Следовательно, по теореме
Пифагора из
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании прямой призмы лежит равнобедренная
трапеция
с основаниями
и
Точка
делит ребро
в отношении
а точка
— середина ребра
а) Докажите, что плоскость делит ребро
пополам.
б) Найдите площадь сечения призмы плоскостью если
Источники:
а) Так как и
то грани
и
параллельны. Следовательно, плоскость
пересечет их по параллельным
прямым. Значит, плоскость
пересечет грань
по прямой
где
— точка на ребре
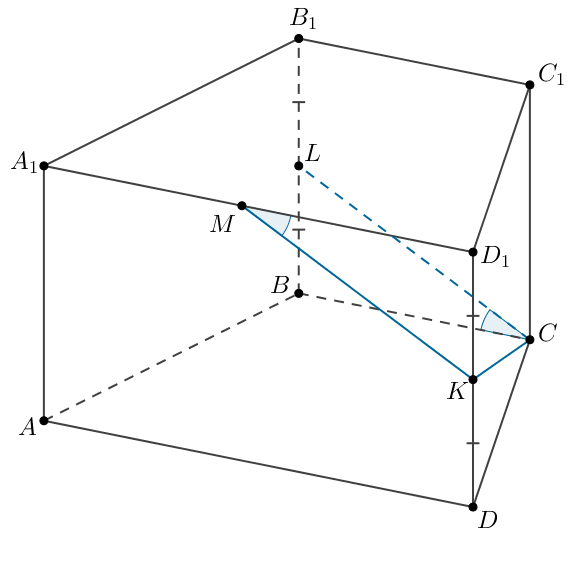
Из условия следует, что Пусть также
Углы
и
равны как углы между попарно параллельными
прямыми. Следовательно, по катету и острому углу равны
и
так как
Следовательно,
Значит,
— середина ребра
Что и требовалось
доказать.
б) Достроим сечение. Продлим до пересечения с прямой
в точке
Тогда точка
являющаяся точкой пересечения
и
является
одной из вершин сечения призмы плоскостью
Следовательно,
— сечение призмы плоскостью
Так как и
то
— параллелограмм.
Следовательно,
Следовательно,
равнобедренный
с углом
значит, он равносторонний и
Следовательно,
По теореме Пифагора
Так как
и
то
— прямоугольник,
следовательно,
и
прямоугольный с
Также
следовательно,
откуда
По теореме Пифагора
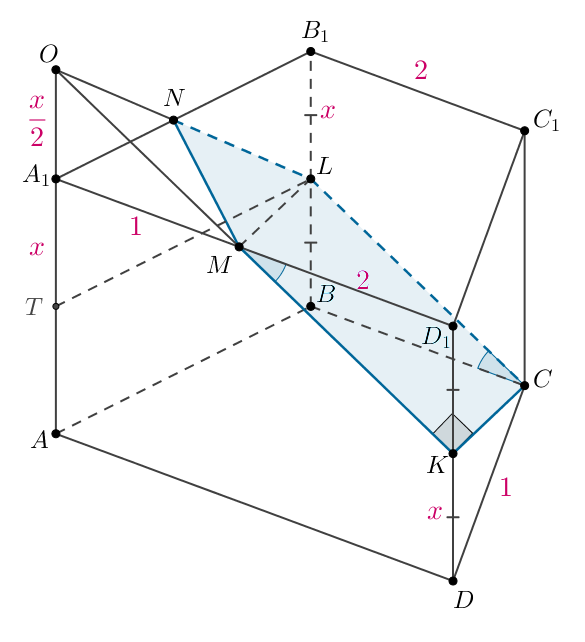
Проведем Следовательно, треугольник
прямоугольный и по
теореме Пифагора
Тогда по теореме Пифагора для получаем
Из следует, что
следовательно,
Отсюда
так как
прямоугольный.
Так как то
Следовательно, так как к тому же — прямоугольник, получаем, что
площадь сечения равна
б)
Ошибка.
Попробуйте повторить позже
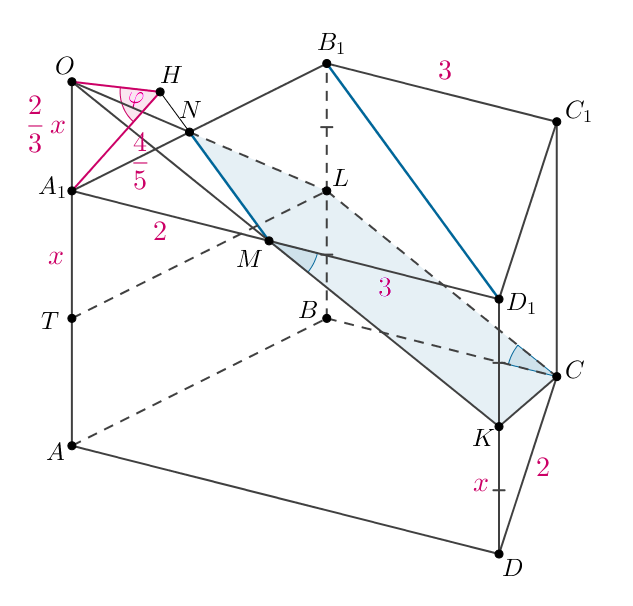
В основании прямой призмы лежит равнобедренная
трапеция
с основаниями
и
Точка
делит ребро
в отношении
а точка
— середина ребра
а) Докажите, что плоскость параллельна прямой
б) Найдите тангенс угла между плоскостью и плоскостью основания
призмы, если
Источники:
а) Так как и
то грани
и
параллельны. Следовательно, плоскость
пересечет их по параллельным
прямым. Значит, плоскость
пересечет грань
по прямой
где
— точка на ребре
Продлим
до пересечения с
прямой
в точке
Тогда точка
являющаяся точкой пересечения
и
является одной из вершин сечения призмы плоскостью
Следовательно,
— сечение призмы плоскостью
Так как то достаточно доказать, что
Из условия следует, что Пусть также
Углы
и
равны как углы между попарно параллельными прямыми.
Следовательно, по катету и острому углу равны
и
так как
Следовательно,
Значит,
— середина ребра

следовательно,
откуда
следовательно,
значит,
можно обозначить
По обратной теореме Фалеса, так как то
Следовательно,
откуда
Что и
требовалось доказать.
б) Так как и
то
—
параллелограмм. Следовательно,
Следовательно,
равнобедренный с углом
значит, он равносторонний и
Следовательно,
По теореме Пифагора
Так как
и
то
— прямоугольник,
следовательно,
и
прямоугольный с
Также
По теореме Пифагора
Проведем Следовательно, треугольник
прямоугольный и по
теореме Пифагора
Тогда по теореме Пифагора для получаем
Так как — линия пересечения плоскостей
и
то
проведем
Тогда по теореме о трех перпендикулярах
Следовательно,
— угол между
и
Его тангенс
равен
Следовательно, нужно найти
Заметим, что так как равносторонний и
то
следовательно,
лежит на продолжении отрезка
за точку
Рассмотрим По теореме косинусов
Тогда по теореме синусов из этого же треугольника
Из прямоугольного имеем
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
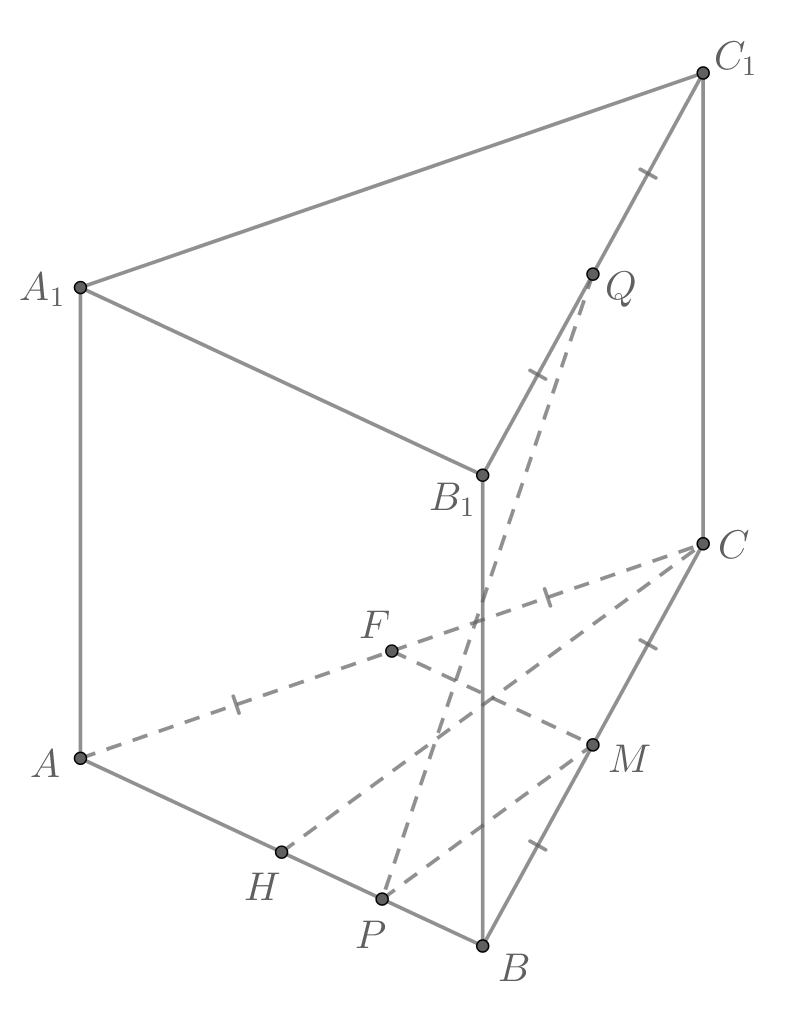
В основании прямой призмы лежит равнобедренный
треугольник
с основанием
Точка
делит ребро
в
отношении
а точка
— середина ребра
Через
середину
ребра
провели плоскость
перпендикулярную отрезку
а) Докажите, что плоскость параллельна ребру
б) Найдите отношение, в котором плоскость делит отрезок
считая от
точки
если известно, что
Источники:
а) Пусть — высота треугольника
Тогда
и медиана. Так
как
а
то имеем
Тогда
— средняя линия треугольника
Тогда
Пусть — средняя линия треугольника
при этом
лежит на
По теореме о трех перпендикулярах Тогда и
Таким образом, если плоскость перпендикулярна
то и любая прямая
из этой плоскости должна быть перпендикулярна
В частности, прямая, по
которой пересекаются
и
Тогда это в точности прямая
Значит,
б) Пусть пересекает
в точке
Тогда в прямоугольном треугольнике
отрезок
— высота. Тогда
Заметим, что а
Также
Из прямоугольного треугольника имеем:
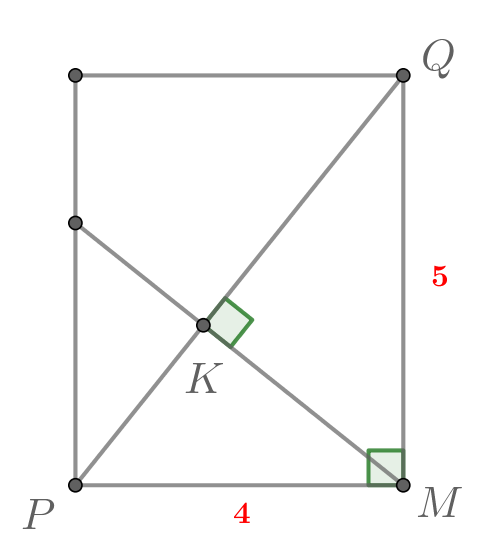
Тогда Значит,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
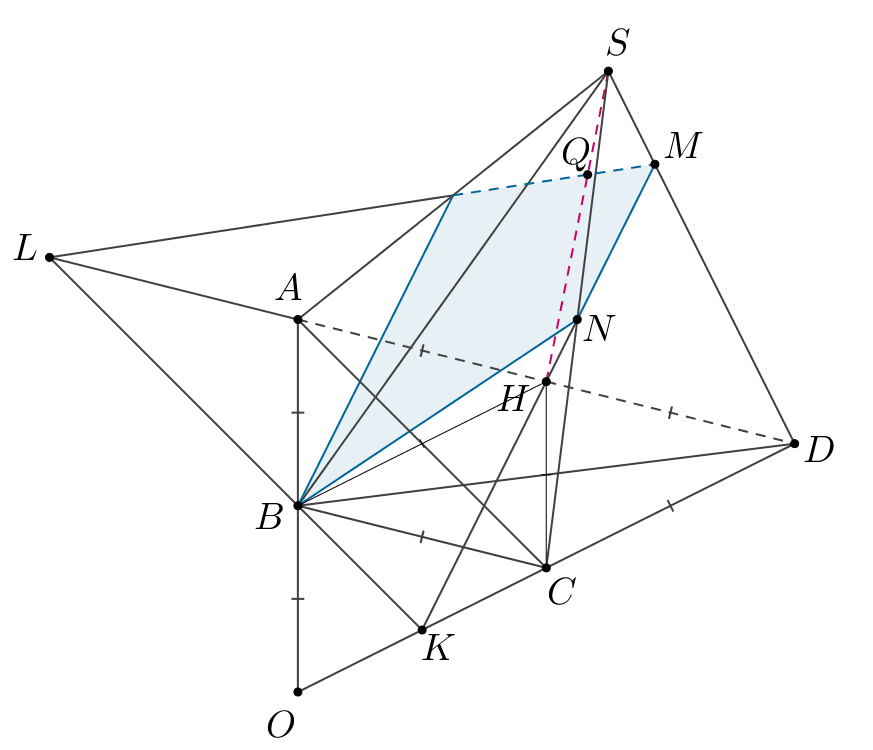
Ошибка.
Попробуйте повторить позже
Bсе боковые ребра четырехугольной пирамиды равны
— стороне
основания
Стороны
и
вдвое меньше стороны
a) Докажите, что высота пирамиды, опущенная из вершины проходит через
середину
б) В каком отношении, считая от точки плоскость
делит высоту
пирамиды, если
— середина
а точка
делит ребро
в отношении
считая от точки
Источники:
а) Так как боковые ребра пирамиды равны, то основание высоты пирамиды из
точки является центром описанной около
окружности. Следовательно,
четырехугольник
— вписанный.
Пусть Так как
равнобедренный
то
и
Так как
вписанный, то во-первых
а во-вторых
как вписанные
углы, опирающиеся на одну дугу
Отсюда
так как
равнобедренный.
Следовательно, Таким образом,
следовательно,
С учетом
получаем, что
—
трапеция, а так как
то это равнобедренная трапеция.
Пусть — точка пересечения прямых
и
Так как
и
то
— средняя линия
Следовательно,
откуда
равносторонний, следовательно,
Тогда если
— середина
то
—
равнобедренные с углом
следовательно, это равносторонние треугольники, и
Значит, точка
равноудалена от всех вершин
трапеции
следовательно,
— центр описанной около
окружности. А так как выше мы сказали, что основание высоты пирамиды
опущенной из вершины
— центр описанной около основания
окружности, то
и есть основание этой высоты. Что и требовалось
доказать.
б) Пусть прямая пересекает
в точке
Тогда
По
теореме Менелая для
и прямой
получаем
Отсюда можно принять
тогда
и
Следовательно, плоскость пересекает плоскость
по прямой
Пусть эта прямая пересекает прямую
в точке
Тогда по теореме
Менелая для
и прямой
получаем

Следовательно,
тогда
откуда
Следовательно,
Так как то плоскость
пересекает плоскость
по
прямой
Пусть
Тогда
— искомое отношение. По
теореме Менелая для
и прямой
получаем
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан тетраэдр На ребре
выбрана точка
так, что
Также на ребрах
и
выбраны точки
и
соответственно
так, что
— квадрат со стороной 3.
а) Докажите, что
б) Найдите объем пирамиды если объем тетраэдра
равен
100.
Источники:
а) Так как — квадрат, то имеем:
Докажем, что Аналогично будет доказываться, что
Рассмотрим плоскости
и
Их линии пересечения
и
либо параллельны друг другу, либо пересекаются в одной
точке. Так как две из трех линий
и
друг другу параллельны, то и
третья линия
им параллельна. Следовательно,
Значит и
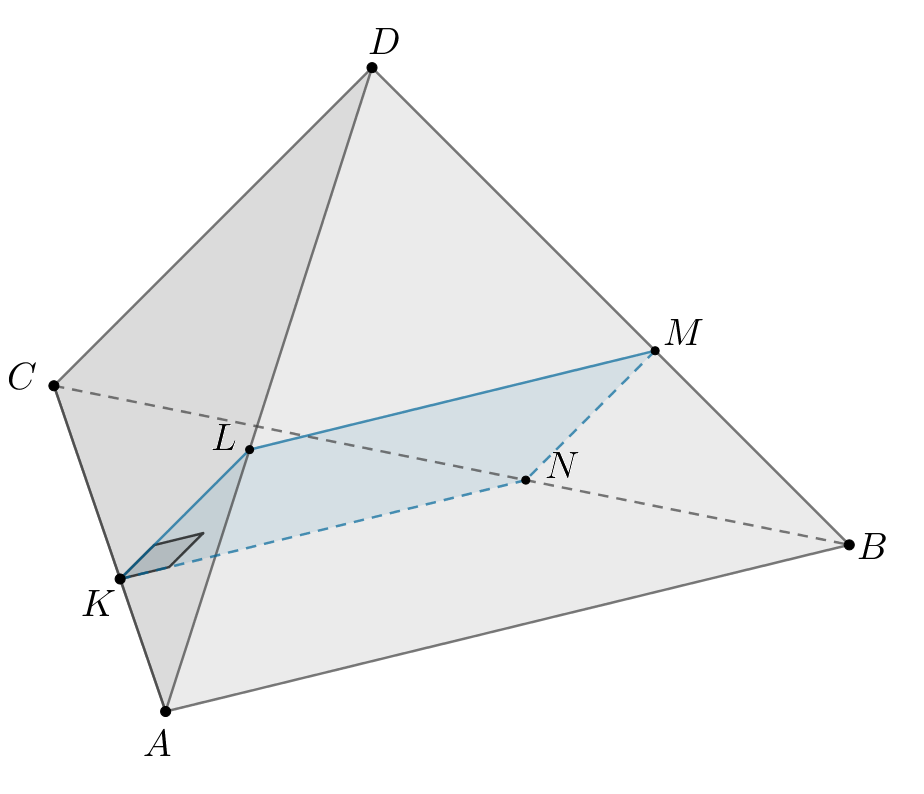
Из параллельности выше следует, что и
Следовательно,
Так как — квадрат, то
следовательно,
Что и требовалось доказать.
б) Докажем следующее утверждение. Если и
— противоположные ребра
тетраэдра,
— расстояние между ними,
— угол между ними, то объем этого
тетраэдра равен
Рассмотрим призму в основании которой лежит
четырехугольник
диагонали которого соответственно равны и
параллельны двум противоположным ребрам данного тетраэдра:
Тогда расстояние между основаниями призмы равно Значит, объем этой
призмы равен
![]()
Распишем, чему равен объем данного тетраэдра
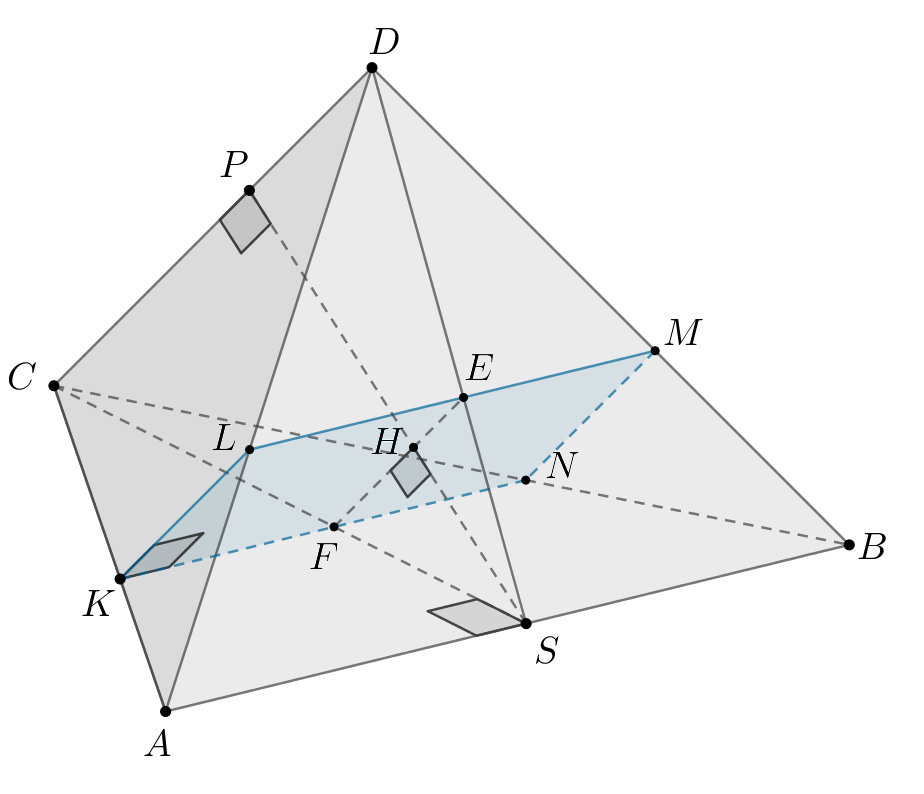
Заметим, что так как то расстояние от любой точки прямой
до этой плоскости будет одинаковым. Аналогично, так как
то
расстояние от любой точки прямой
до этой плоскости будет одинаковым.
Найдем расстояние от прямой
до этой плоскости. Оно будет являться
высотой пирамиды
Проведем Тогда
Проведем
Пусть
Далее имеем:
Тогда и
— искомое расстояние.
Из следует, что
Аналогично получаем
Из доказанной формулы следует, что объем тетраэдра равен
По теореме Фалеса имеем:
Отсюда получаем
Следовательно, объем пирамиды равен
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан тетраэдр На ребре
выбрана точка
так, что
Также на ребрах
и
выбраны точки
и
соответственно
так, что
— квадрат со стороной 2.
a) Докажите, что
б) Найдите расстояние от точки до плоскости
если известно, что
объем тетраэдра
равен 25.
Источники:
а) Так как — квадрат, то
Докажем, что Аналогично будет доказываться, что
Рассмотрим плоскости
и
Их линии пересечения
и
либо параллельны друг другу, либо пересекаются в одной
точке. Так как две из трех линий
и
друг другу параллельны, то и
третья линия
им параллельна. Следовательно,
Значит и Тогда по теореме Фалеса
Что и требовалось доказать.
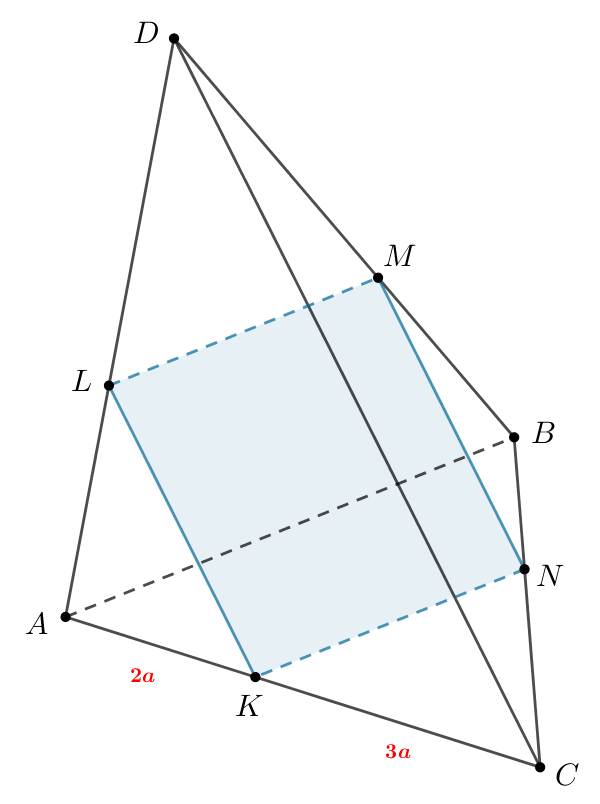
б) По условию — квадрат, поэтому
В пункте а) мы
доказали, что
Значит,
В плоскости проведем перпендикуляр
к
Рассмотрим
плоскость
Прямая
лежит в ней, при этом
Также
прямая
лежит в
при этом
Значит,
Тогда
В плоскости проведем
Тогда

Значит,
Рассмотрим треугольники и
Они подобны, так как имеют общий
угол
и
Тогда
Рассмотрим треугольники и
Они подобны, так как имеют общий
угол
и
Тогда
Значит,

Прямая параллельна плоскости
следовательно, расстояние от
точки
до
равно расстоянию от прямой
до
Заметим, что так как лежит в плоскости
а значит
Также
по построению, а значит
Таким
образом,
Тогда если
— точка пересечения
и
то
расстояние от
до
равно
Пусть в плоскости точка
— это точка пересечения прямых
и
в плоскости
точка
— это точка пересечения прямых
и
Тогда
— это точка пересечения
и
в плоскости
Прямые так как
Значит,
Таким образом, расстояние от точки до плоскости
равно
5,4.
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан тетраэдр На ребре
выбрана точка
так, что
Также на ребрах
и
выбраны точки
и
соответственно
так, что
— квадрат со стороной 3.
а) Докажите, что ребра и
взаимно перпендикулярны.
б) Найдите расстояние от точки до плоскости
если объем
тетраэдра
равен 100.
Источники:
а) Так как — квадрат, то
Докажем, что Аналогично будет доказываться, что
Рассмотрим плоскости
и
Их линии пересечения
и
либо параллельны друг другу, либо пересекаются в одной
точке. Так как две из трех линий
и
друг другу параллельны, то и
третья линия
им параллельна. Следовательно,
Значит и Так как
— квадрат, то
Следовательно,
Что и требовалось доказать.
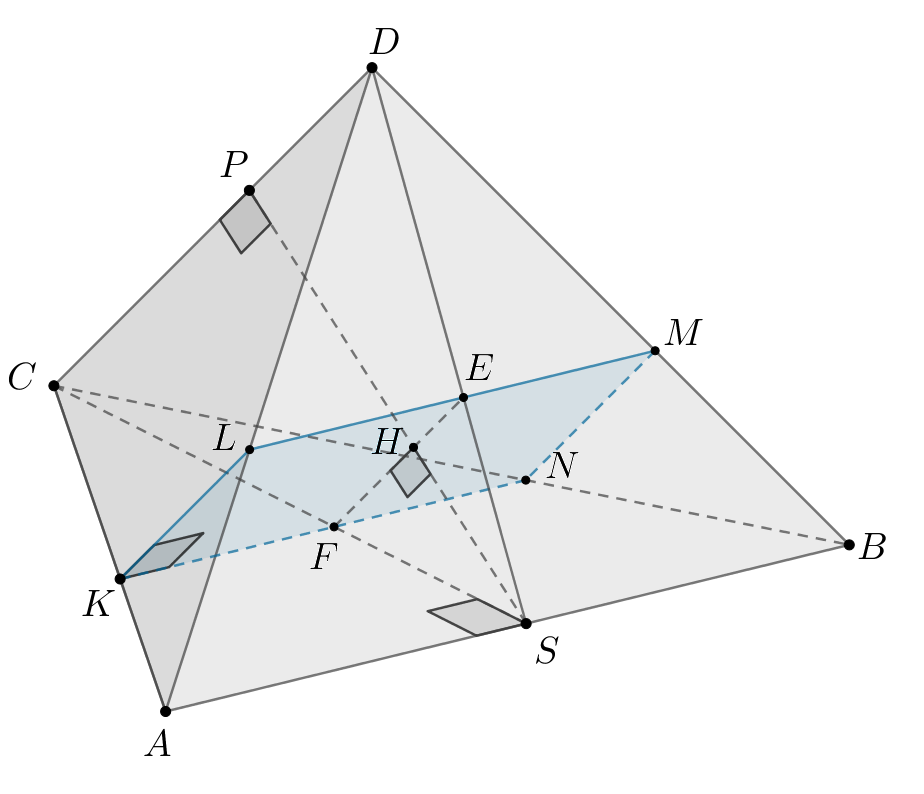
б) Докажем мини-задачу: если и
— противоположные ребра тетраэдра,
— расстояние между ними,
— угол между ними, то объем этого тетраэдра равен
Рассмотрим призму в основании которой лежит
четырехугольник
диагонали которого соответственно равны и
параллельны двум противоположным ребрам данного тетраэдра:
Тогда расстояние между основаниями призмы равно
Значит, объем этой призмы
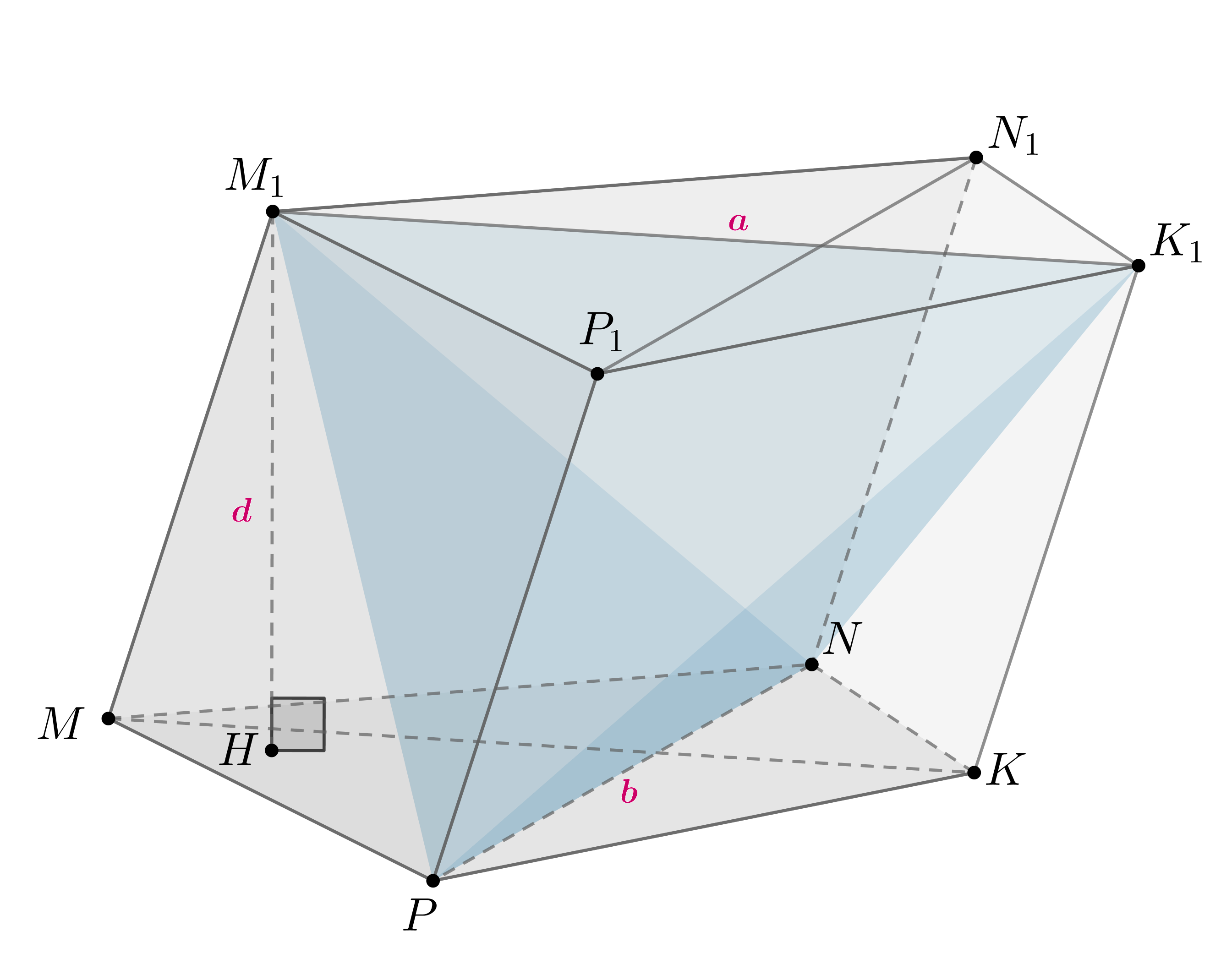
Распишем, чему равен объем данного тетраэдра

Заметим, что так как то расстояние от любой точки прямой
до этой плоскости будет одинаковым.
Проведем Тогда
Проведем
Пусть
Тогда
так как
и
Следовательно,
— искомое расстояние.
Из следует, что
Следовательно,
Аналогично
откуда
Из доказанной формулы следует, что объем тетраэдра равен
Так как по теореме Фалеса то
Тогда
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана пирамида в основании которой лежит квадрат
Сечение
пирамиды — четырехугольник
причем точки
лежат на
ребрах
и
соответственно. Известно, что
и
— середины
ребер
и
а
а) Докажите, что — трапеция и основания трапеции относятся как
б) Известно, что угол между плоскостью трапеции и плоскостью
основания
равен
Найдите высоту пирамиды
если
площадь квадрата
равна 32, а площадь четырехугольника
равна
Источники:
а) Будем пользоваться следующей теоремой: если нам даны три попарно пересекающиеся плоскости, то их линии пересечения либо параллельны, либо все пересекаются в одной точке. Из этой теоремы следует, что если две из трех линий пересечения параллельны, то третья линия пересечения также им параллельна.
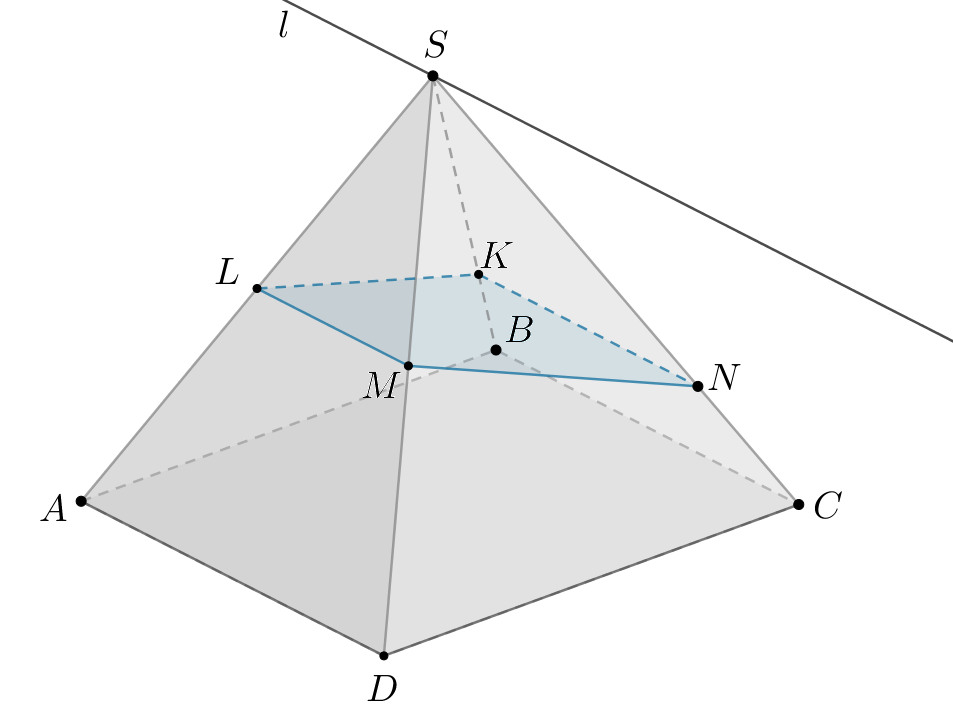
Так как — линия пересечения плоскостей
и
— линия пересечения плоскостей
и
и
то
— линия пересечения плоскостей
и
— параллельна
Теперь рассмотрим три плоскости:
и
Так как
и
— середины
и
то
следовательно, линия пересечения
плоскостей
и
— прямая
Тогда по теореме Фалеса
Далее имеем:
значит,
Но по
условию
— квадрат, следовательно,
следовательно,
откуда следует, что
— трапеция. Также отсюда
следует, что
Что и требовалось доказать.
б) Рассмотрим три плоскости
и
и их линии
пересечения
и
Так как
то
Пусть
Проведем и
Тогда по теореме о трех перпендикулярах
Следовательно,
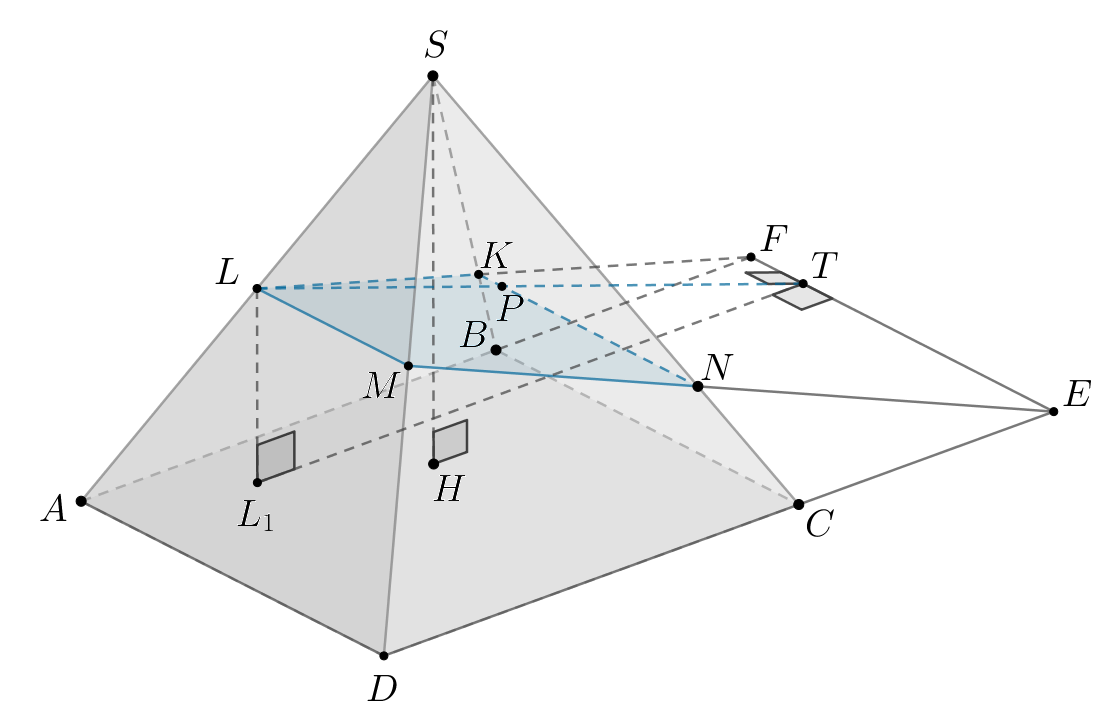
Пусть Тогда так как
то
следовательно,
— высота трапеции
По теореме Фалеса
Найдем последнее отношение.
По теореме Менелая для и прямой
имеем:
Следовательно,
По теореме Менелая для и прямой
имеем:
Следовательно, значит,
Проведем Тогда
следовательно,
— искомая
высота. Пусть
Тогда
Так как
то
Следовательно,
Также заметим, что из следует, что
Тогда
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан тетраэдр причем
а грани
и
перпендикулярны. На ребрах
и
отмечены точки
и
соответственно так, что
а) Докажите, что плоскость перпендикулярна ребру
б) Найдите длину отрезка, по которому плоскость пересекает грань
Источники:
а) По условию и
— правильные. Проведем
Тогда
Тогда получаем, что
следовательно, по обратной теореме Фалеса
Откуда следует,
что
А так как
то
значит,
Проведем Тогда
следовательно,
значит, по обратной теореме Фалеса
Следовательно,
Значит, ребро перпендикулярно двум пересекающимся прямым
и
следовательно,
Что и требовалось доказать.
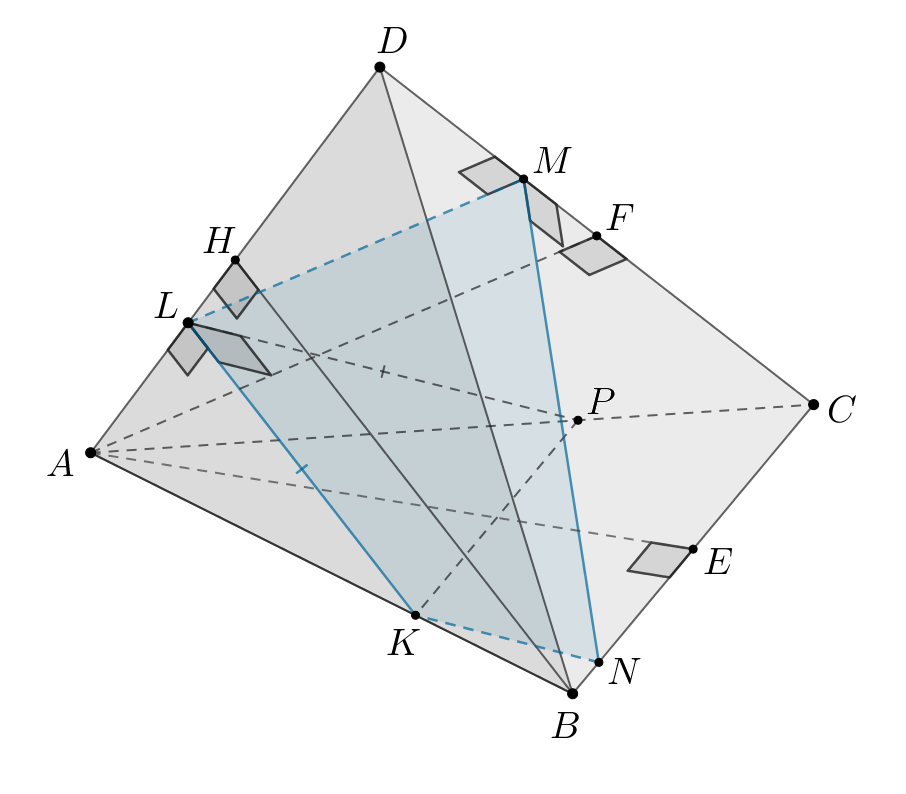
б) Пусть Тогда
по двум сторонам и углу
между ними, следовательно,
Тогда
— угол между
плоскостями
и
Тогда мы получаем равнобедренный
прямоугольный треугольник
следовательно,
Найдем
Следовательно, Заметим, что
следовательно,
Отсюда
Так как то плоскость
пересечет грань
по
отрезку
Заметим, что — равнобедренные. Пусть
Пусть
также
— середина основания
Тогда
Следовательно,
Но также имеем
Так как то по теореме косинусов из
имеем
Заметим, что — искомый отрезок.
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан тетраэдр причем
а грани
и
перпендикулярны. На ребрах
и
отмечены точки
и
соответственно так, что
а) Докажите, что плоскость перпендикулярна ребру
б) Найдите длину отрезка, по которому плоскость пересекает грань
Источники:
а) Заметим, что и
— правильные. Проведем
Тогда
откуда
Тогда мы имеем
следовательно, по обратной теореме Фалеса
Значит,
А так
как
то
откуда следует, что
так как
следовательно,
то есть
Таким образом, ребро перпендикулярно двум пересекающимся
прямым
и
следовательно,
Что и требовалось
доказать.
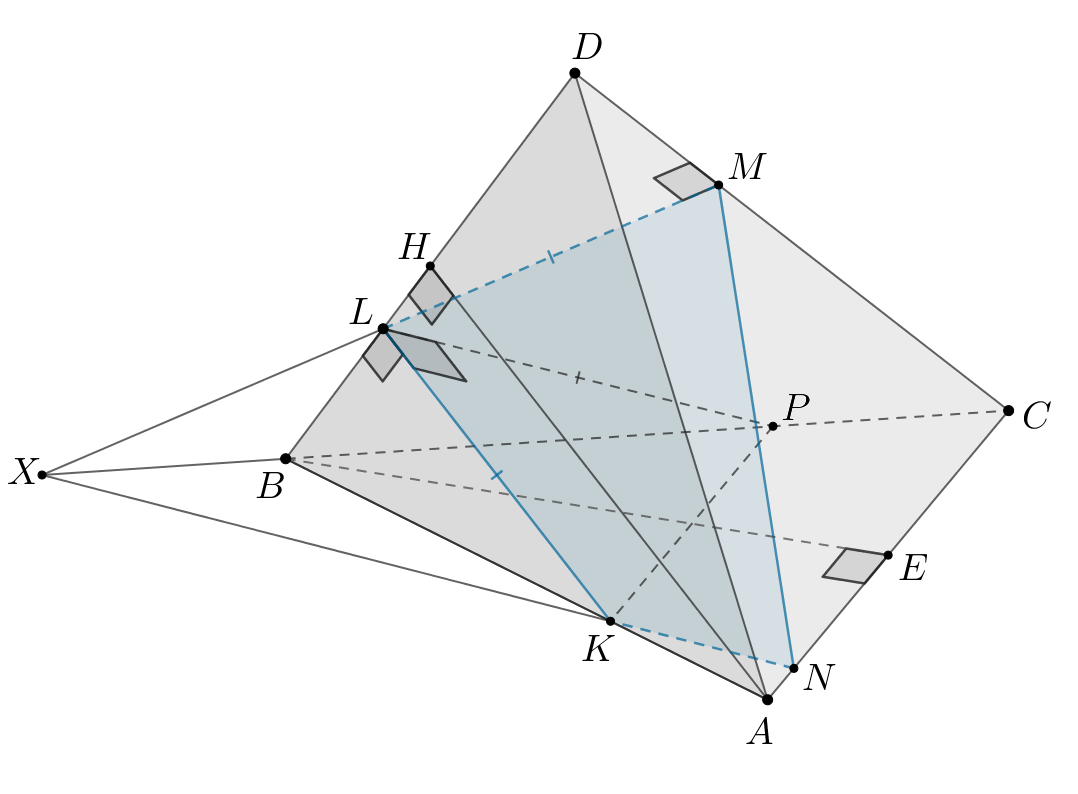
б) Пусть Тогда
Следовательно,
—
искомый отрезок.
Отметим Тогда
следовательно,
Тогда по определению
— угол между плоскостями
и
Тогда — прямоугольный и равнобедренный, следовательно,
А так как
то
Отсюда
следовательно,
Найдем Имеем
Тогда
По теореме Менелая для и прямой
получаем
По теореме Менелая для и прямой
получаем
Следовательно,
Проведем — медиану и высоту равнобедренного треугольника
Тогда если обозначить
то
Тогда по теореме
косинусов для
имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана пирамида в основании которой лежит квадрат
Сечение
пирамиды — четырехугольник
причем точки
лежат на
ребрах
и
соответственно. Известно, что
и
— середины
ребер
и
а
а) Докажите, что — трапеция и основания трапеции относятся как
б) Известно, что угол между плоскостью трапеции и плоскостью
основания
равен
Найдите высоту пирамиды
если
площадь квадрата
равна 56, а площадь четырехугольника
равна
Источники:
а) Будем пользоваться следующей теоремой: если нам даны три попарно пересекающиеся плоскости, то их линии пересечения либо параллельны, либо все пересекаются в одной точке. Из этой теоремы следует, что если две из трех линий пересечения параллельны, то третья линия пересечения также им параллельна.
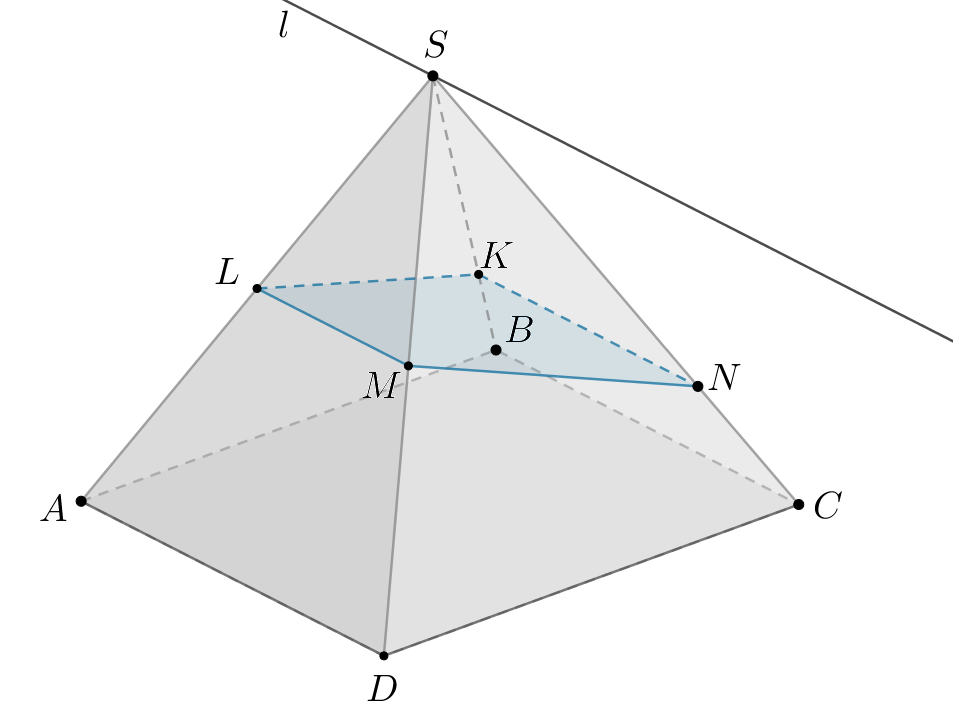
Так как — линия пересечения плоскостей
и
— линия пересечения плоскостей
и
и
то
— линия пересечения плоскостей
и
— параллельна
Теперь рассмотрим три плоскости:
и
Так как
и
— середины
и
то
следовательно, линия пересечения
плоскостей
и
— прямая
Тогда по теореме Фалеса
Далее имеем:
значит,
Но по
условию
— квадрат, следовательно,
следовательно,
откуда следует, что
— трапеция. Также отсюда
следует, что
Что и требовалось доказать.
б) Рассмотрим три плоскости
и
и их линии
пересечения
и
Так как
то
Пусть
Проведем и
Тогда по теореме о трех перпендикулярах
Следовательно,
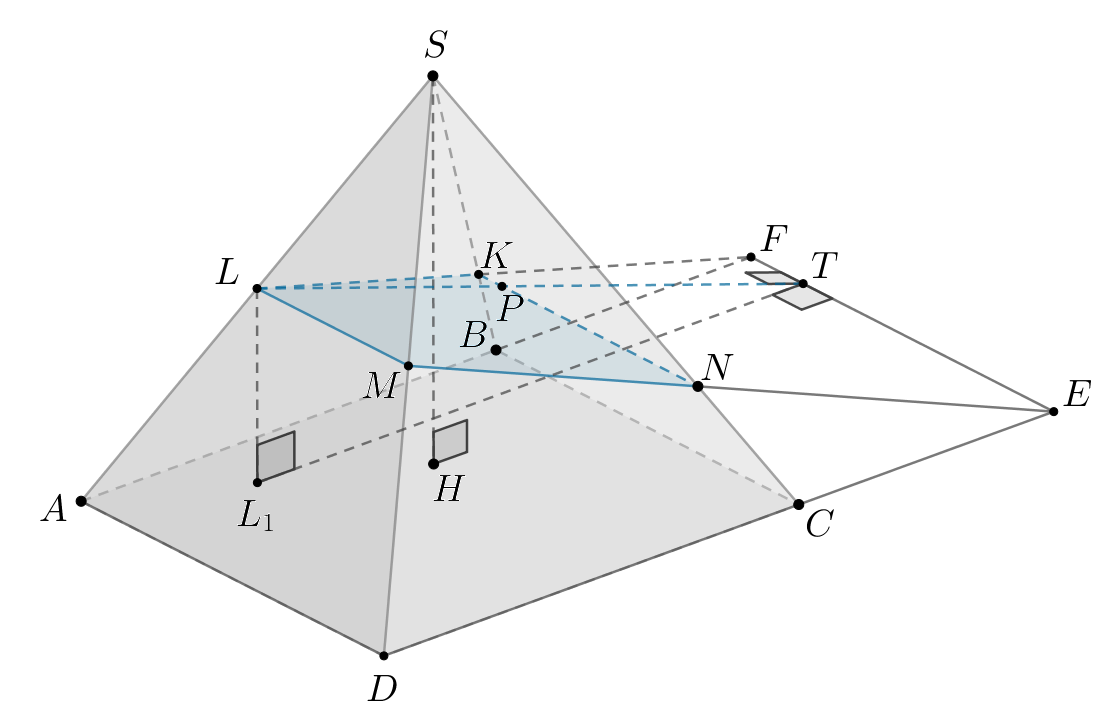
Пусть Тогда так как
то
следовательно,
— высота трапеции
По теореме Фалеса
Найдем последнее отношение.
По теореме Менелая для и прямой
имеем:
Следовательно,
По теореме Менелая для и прямой
имеем:
Следовательно, значит,
Проведем Тогда
следовательно,
— искомая
высота. Пусть
Тогда
Так как
то
Следовательно,
Также заметим, что из следует, что
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана пирамида в основании которой лежит прямоугольник
Сечение пирамиды — трапеция
причем точки
лежат на
ребрах
и
соответственно. Известно, что основания этой трапеции
а
а) Докажите, что точки и
— середины ребер
и
б) — точка пересечения диагоналей прямоугольника
а
—
высота пирамиды
Найдите
если известно, что площадь
прямоугольника
равна 48, а площадь трапеции
равна
24,5.
Источники:
а) Будем пользоваться следующей теоремой: если нам даны три попарно пересекающиеся плоскости, то их линии пересечения либо параллельны, либо все пересекаются в одной точке. Из этой теоремы следует, что если две из трех линий пересечения параллельны, то третья линия пересечения также им параллельна.
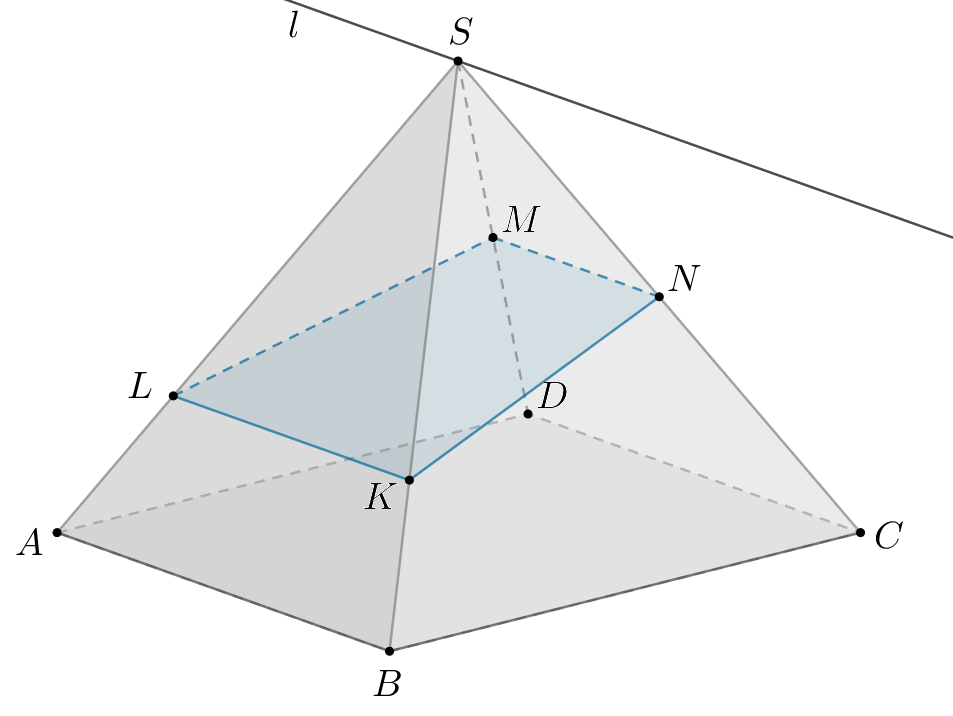
Так как по условию то есть две линии пересечения плоскостей
и
из трех параллельны, то
и
параллельны
линии пересечения плоскостей
и
Но так как
— линия
пересечения плоскостей
и
— линия пересечения плоскостей
и
и
то
— линия пересечения плоскостей
и
— параллельна
Следовательно,
Значит, и
Так как
то
Следовательно,
Значит,
То есть
Но
следовательно,
Отсюда следует, что
и
— середины
и
Что и требовалось
доказать.
б) Так как
то
Так как основание высоты
пирамиды
— это центр прямоугольника
то боковые ребра
пирамиды равны друг другу:
Из этого следует, что
Следовательно,
значит,
то
есть трапеция
равнобокая.
Проекция на плоскость
— трапеция
где
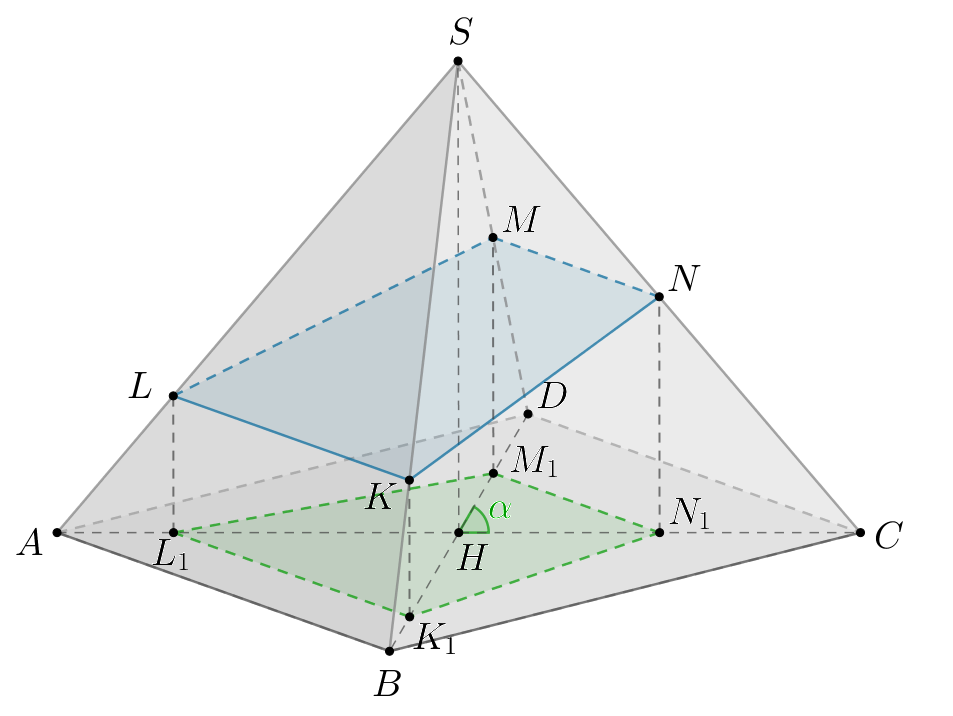
Пусть
Тогда
Пусть
Тогда
следовательно,
Заметим, что
следовательно,
Как известно, отношение площади проекции многоугольника к площади самого многоугольника равно косинусу угла между плоскостью проекции и плоскостью многоугольника. Следовательно,
равно косинусу угла между плоскостями и
Построим этот
угол.
Проведем через точку
Тогда
и
— середины
и
соответственно. Тогда
и
пересекает
и
соответственно в
точках
и
причем по теореме Фалеса
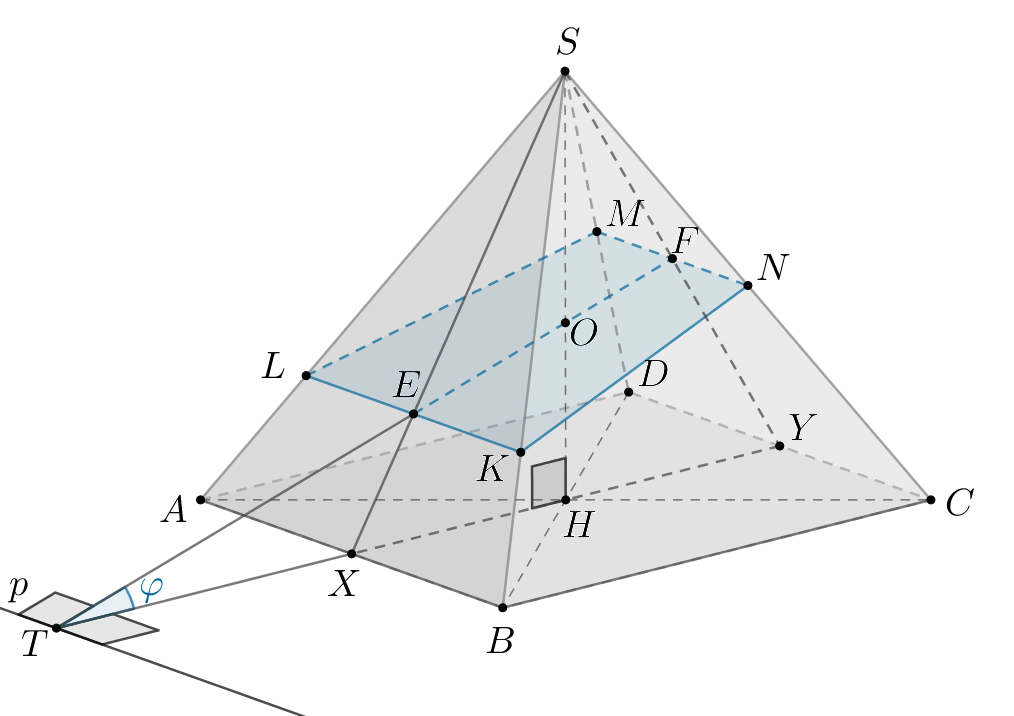
Пусть Тогда точка
лежит на линии пересечения
плоскостей
и
По теореме, которую мы использовали в пункте а),
получаем, что
Пусть По теореме о трех перпендикулярах
(так как
). Следовательно, по определению
— угол между плоскостями
и
Так как
то
Рассмотрим и прямую
По теореме Менелая имеем:
По теореме Менелая для и прямой
Следовательно,
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана четырехугольная пирамида Четырехугольник
— трапеция с большим основанием
отрезок
— ее средняя линия. Диагонали трапеции пересекаются в точке
Отрезок
содержится в плоскости
параллельной
а) Докажите, что сечение пирамиды плоскостью — трапеция.
б) Найдите площадь сечения пирамиды плоскостью если
а
Источники:
а) Пусть — точки пересечения
с диагоналями трапеции. Так как
то проведем
и получим
сечение пирамиды плоскостью
— четырехугольник
. Докажем, что это трапеция.
Так как лежит в
и
то
Следовательно,
пересечет плоскость, в которой лежит
по
прямой, параллельной
Следовательно,
Осталось доказать, что не параллельна
Действительно, так как
то
Тогда, так как
то
следовательно,
не параллельна
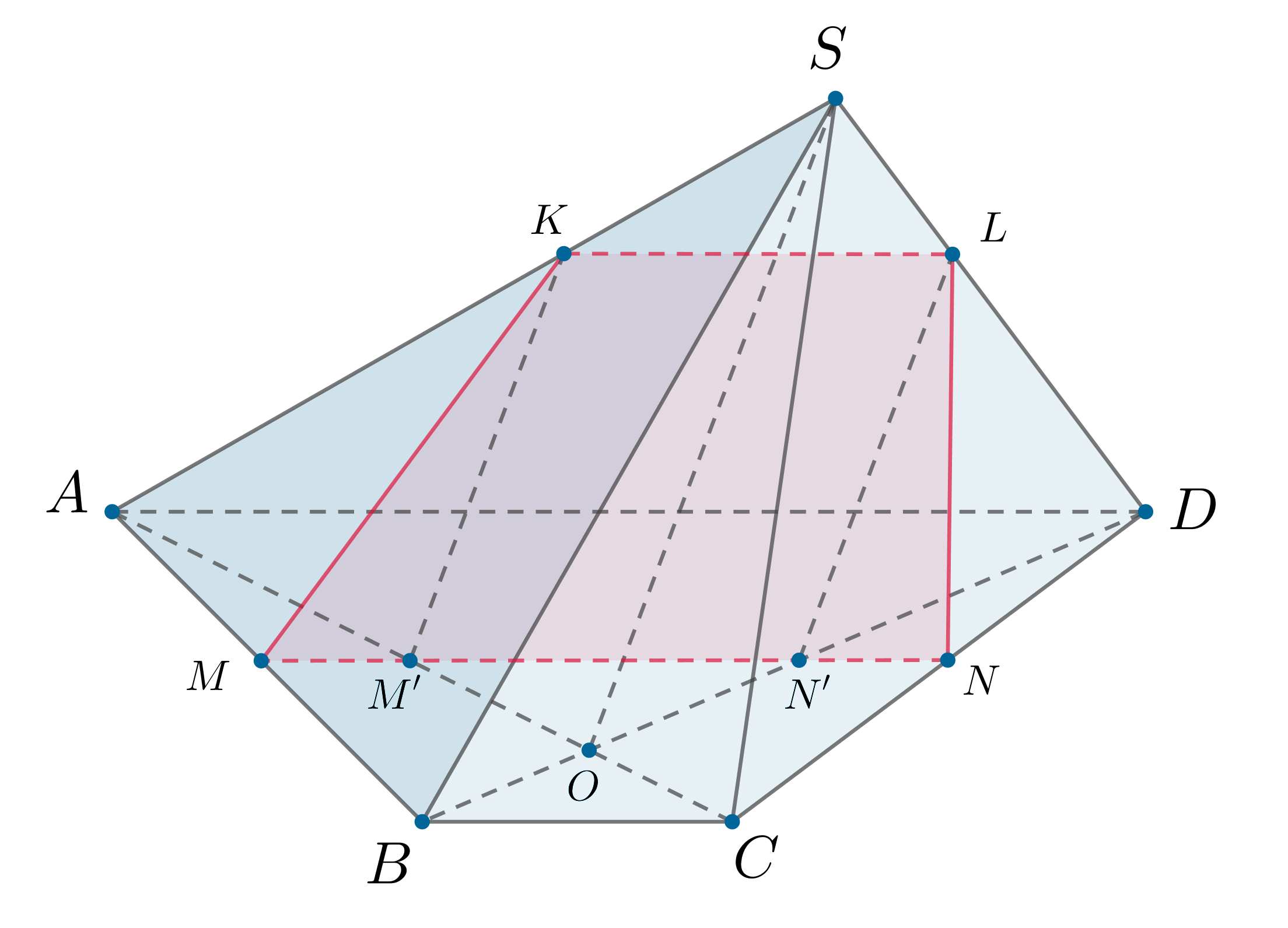
б) Так как то пусть
Тогда
Для точки имеем:
Из условия задачи следовательно, по теореме Фалеса
Значит а
Так как
то
следовательно,
— высота
трапеции, находящейся в сечении.
Тогда искомая площадь сечения равна
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Точка — середина ребра
правильной четырехугольной пирамиды
с основанием
Точка
принадлежит ребру
причем
a) Докажите, что плоскость параллельна прямой
б) Найдите площадь сечения пирамиды плоскостью если все ребра пирамиды равны 6.
Источники:
а) Назовем плоскость плоскостью
Пусть
— высота пирамиды, тогда
Пусть
Прямые
и
лежат в одной плоскости
следовательно, если требуется доказать, что
то нужно доказать, что
По теореме Менелая для и прямой
По теореме Менелая для и прямой
Следовательно, если то
значит,
и
Следовательно, по обратной теореме Фалеса
б) Если то четырехугольник
— сечение пирамиды плоскостью
Будем искать площадь сечения
через площадь проекции этого многоугольника на плоскость основания пирамиды и угол между плоскостями сечения и
основания.
Найдем — косинус угла между плоскостями
и
Проведем
тогда по ТТП
и
Ищем сначала
— прямоугольный (так как диагонали квадрата в основании правильной пирамиды взаимно перпендикулярны),
значит,
Тогда
Так как все ребра пирамиды равны, то Следовательно,
Так как
то
Следовательно,
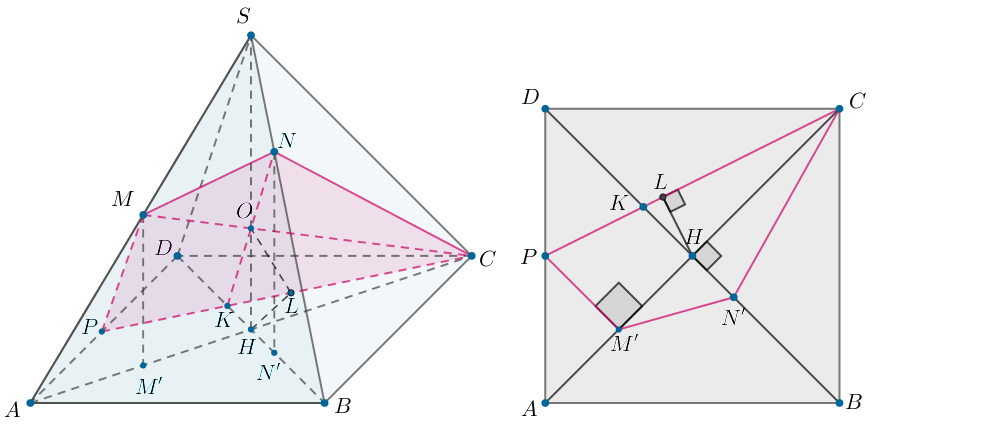
Теперь спроецируем на плоскость
Тогда
— проекция точки
и середина
— проекция
точки
причем
Получили четырехугольник
Так как то
следовательно,
— середина
Следовательно,
—
средняя линия в
значит,
Тогда
Так как то
следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



