Межрегиональная им. И. Я. Верченко (криптография) —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Межрегиональная им. И. Я. Верченко (криптография)

Тема Межрегиональная им. И. Я. Верченко (криптография)

Межрегиональная им. И. Я. Верченко (криптография)

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Разделы подтемы Межрегиональная им. И. Я. Верченко (криптография)

Отбор Верченко

Теория чисел на Верченко

Планиметрия на Верченко

Уравнения и системы на Верченко

Комбинаторика на Верченко

Многочлены на Верченко

Последовательности, функции и их кодирование на Верченко

Подтемы раздела межрегиональная им. и. я. верченко (криптография)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#71011

Дана последовательность $a,b ,a ,b,...,a,b 1 1 2 2 k k$ , состоящая из $0$ и $1.$ Пусть $N$ — количество чисел $i$ от $1$ до $k$ таких, что $a = 0 i$ и $bi = 1.$ Докажите, что число последовательностей указанного вида, для которых $N$ нечетно, находится по формуле $2k−1 k−1 2 − 2 .$

Источники: Верченко-2022 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

В задаче есть параметр k, учитывая который строятся последовательности. Увеличив k, несложно построить новую последовательность, не "сломав" старую. Попробуем решить задачу индукцией по k! Докажем, что если утверждение выполняется при k-1, но оно выполняется и при k.

Подсказка 2

Если последовательность из 2k элементов удовлетворяет условию, то какой тогда будет эта последовательность без последнего пары a_k, b_k? Что будет с четностью N?

Подсказка 3

Нам подходят такие последовательности длины 2(k-1), где N четно, а_k = 0 и b_k = 1. А если N нечетно, то какой может быть пара (a_k;b_k)?

Показать доказательство

Применим метод математической индукции по параметру $k$ . При $k= 1$ формула очевидна. Докажем, что если она верна при $k − 1$ , то верна и при $k.$

Искомое число равно числу последовательностей

a1,b1,a2,b2,...,ak−1,bk−1,

(1)

в которых количество $i= 1,2,...k− 1,$ таких, что $ai = 0$ и $bi = 1$ четно (в этом случае пара $(ak,bk)$ может быть только $(0,1))$ плюс количество последовательностей вида (1) в которых количество чисел $i= 1,2,...k− 1,$ таких, что $ai = 0$ и $bi = 1$ нечетно, умноженному на 3 (так как пара $(ak,bk)$ может быть любой из пар $(0,0),(1,0),(1,1)).$ В итоге по предположению индукции нужное число последовательностей будет удовлетворять равенству

( ( )) ( ) 22(k−1)− 22(k−1)−1 − 2k−2 + 3 22(k−1)−1− 2k−2 =22k−1− 2k−1

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#68243

Для входа в университет Криптоландии у каждого студента есть карточка, на которой записана уникальная (у каждого студента своя) последовательность $x1,x2,x3,x4,x5,x6,x7$ из целых чисел от 0 до 5. При входе в университет студент прикладывает карточку к устройству, которое подсчитывает величины $A$ и $B$ по формулам:

A= ((x1 ∗x2)∗ x3)∗x4

B =(x5∘x6)∘x7

Операции $∗$ и $∘$ задаются таблицами (представляющими собой латинские квадраты: у них в каждой строке и каждом столбце числа не повторяются).

$PIC$

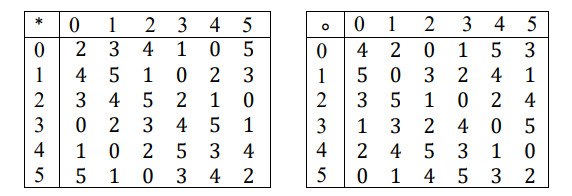
Например, $3∗2 =3,$ $2∘ 4=2.$ Студенту разрешат войти, если $A = B.$

Сколько самое большое может быть студентов в таком университете?

Подсказки к задаче

Подсказка 1

Делать вычисления по этим таблицам точно не хочется, поэтому давайте подумаем. Посмотрите внимательно на строчки и столбцы таблиц...что в них есть примечательного?

Подсказка 2

В каждой строчке и в каждом столбце по одному разу использовано каждое число от 0 до 6) Что это может значить?

Подсказка 3

Например, для любого x от 0 до 6 найдется такой y, что каждая из этих операций с x и y даст результат который мы хотим, причём y будет однозначно задаваться по таблице) Раскрутите эту идею.

Показать ответ и решение

Если код составлен из чисел от $0$ до $m − 1$ , то для каждого числа

k∈ {0,...,m − 1}

число последовательностей $x1,x2,x3,x4$ , для которых $A = k$ , равно $m3$ , так как при любых заданных $x1,x2,x3$ значение $x4$ определяется в этом случае однозначно.

Аналогично, число последовательностей $x ,x,x 5 6 7$ для которых $B = k$ , равно $m2$ . Тогда общее число последовательностей $x ,x,x ,x,x ,x ,x 1 2 3 4 5 6 7$ , для которых $A= B =k$ , равно $m3m2 = m5$ . Суммируя по $k$ от $0$ до $m − 1$ , получаем ответ: $m6$ .

Ответ:

$66$

Ошибка.
Попробуйте повторить позже

Задача 3#68242

Имеется устройство, которое строит последовательность чисел $x,x ,x ,... 0 1 2$ следующим образом: первые два члена $x 0$ и $x 1$ мы задаем самостоятельно, а последующие члены устройство вычисляет так: $x2 =x0+ 13⋅(x1+ k1),x3 = x1+ 13 ⋅(x2+ k2),...$ Здесь $k1,k2,...$ — – некоторая фиксированная ключевая последовательность. При этом все числа $x0,x1,x2,...$ и $k1,k2,...$ являются целыми, лежащими в пределах от 0 до 32 включительно. (Если в процессе вычислений получится число, превосходящее 32, то результат будет заменен его остатком от деления на 33; например, $16+ 13 ⋅2 =9.)$ С помощью этого устройства построили две последовательности $a0,a1,a2,...$ и $b0,b1,b2,...,$ по первым членам $a0 =1,a1 = 3$ и $b0 =1,b1 =12.$ Верно ли, что найдётся ключевая последовательность $k1,k2,...$ и некоторое целое $t,$ большее 0, такие, что выполняются условия:

a) $bt = at,bt+1 =at+1?$

б) $bt = at+1?$

Решение обоснуйте.

Источники: Верченко-2023 (см. v-olymp.ru)

Подсказки к задаче

Пункт а), подсказка 1

У вас есть равенство двух членов одной последовательности двум другим. А как можно выразить, например предыдущий член последовательности через два соседних? Попробуйте так прийти к противоречию)

Пункт б), подсказка 1

Мы понимаем, что последовательности устроены одинаковым образом, так еще и ключевая последовательность у них одинаковая. Что можно сделать, чтобы вообще исключить эту последовательность?

Пункт б), подсказка 2

Вычесть одну последовательность из другой! По факту, в этой последовательности тогда нужно будет понять, есть там единица, или нет. В таком случае посмотрите на первые члены и на то, по какому модулю у нас все происходит и придите к противоречию)

Показать ответ и решение

а) Для всех $t≥1$

at+1 = at− 1+13(at+ kt),at−1 =at+1− 13(at+kt)

Поэтому, если $bt = at,bt+1 =at+1$ , то $bt−1 =at−1,...b1 = a1,b0 = a0$ , что противоречит условию.

б) Удобно перейти к разностям полублоков $zt = bt− at$ (везде далее действия с полублоками (умножение, сложение и вычитание) производятся по модулю $M$ ) и выяснить, может ли 1 появиться в ${z} t$ . Из уравнения шифрования

bt+1 = bt−1+ 13(bt+kt),t≥ 1

a =a + 13(a +k ),t≥ 1 t+1 t−1 t t

получаем после вычитания

zt+1 = zt−1+ 13zt,t≥1,

что последовательность разностей не зависит от ключа $kt$ . По условию $(z0,z1)= (0,9),(z0,z1,M )= 3$ , поэтому все члены последовательности будут делиться на $3$ , и единицы там не будет.

Ответ:

а) нет

б) нет

Ошибка.
Попробуйте повторить позже

Задача 4#68241

Пусть $x =(x ,...,x ) 1 8$ — двоичный вектор длины 8. Обозначим $xd$ — циклический сдвиг вектора $x$ на $d$ позиций вправо. Например, если $x =(1,0,0,0,0,0,0,0),$ то $2 x = (0,0,1,0,0,0,0,0).$ При этом считаем, что $0 x = x.$ Под суммой векторов $x= (x1,...,x4)$ и $y =(y1,...,y4)$ будем понимать вектор

x +y =(x1⊕ y1,x2⊕ y2,x3⊕ y3,x4⊕ y4)

Здесь $⊕$ — стандартная операция сложения битов: $0 ⊕0 =1⊕ 1= 0,$ $0⊕ 1= 1⊕0 =1.$ Пусть

1 4 x= v+ v + v

Найдите $d1,...,dn$ такие, что при любом исходном векторе $v$ выполняется равенство

v =xd1 + ⋅⋅⋅+ xdn

Источники: Верченко-2023 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Пупупу… Какие-то непонятные векторы, с которыми работать не очень понятно как, да и просто непривычно! На что можно заменить любой вектор, чтобы с этим было удобнее работать?

Подсказка 2

Да, можно заменить любой вектор длины a на многочлен, степени одночленов которого — это числа от 0 до a(включительно)! Подумайте, как можно отобразить операцию циклического сдвига на многочлене?

Подсказка 3

Верно, можно просто умножать все его на одночлены на степень, равную величине сдвига и после этого от каждой степени оставлять только остаток по модулю длины вектора! Тогда какому многочлену соответствует вектор x?

Подсказка 4

Да, это многочлен, который состоит из одночленов со степенями 0, 1, 4. А какое условие должно выполняться, чтобы мы нашли многочлен v?

Подсказка 5

Верно, нужно, чтобы произведение многочлена x на многочлен v равнялось единице(учитывая, что можно заменять степени на остаток по модулю введённой степени многочлена)! Осталось найти такой многочлен v, для которого это выполняется!

Показать ответ и решение

Заметим, что $xd+8n = xd$ для любого натурального числа $n$ . Вектору $x = (x ,...,x) 1 8$ взаимно однозначно соответствует многочлен

7 8 x(t)= x1+ x2t+ ...+ x7t + x8t

Тогда циклический сдвиг вектора $x$ на $d$ позиций вправо равносилен умножению многочлена $x(t)$ на $td$ и приведению степеней мономов по модулю $8$ .

Вектору $x =v +v1 +v4$ соответствует многочлен $x(t)= 1+ t+ t4$ . Таким образом, нахождение $d ,...,d 1 n$ таких, что $v =xd1 +...+ xdn$ равносильно нахождению многочлена $v(t)= td1 +...+ tdn$ со свойством $x(t)v(t)= 1$ (с учётом приведения степеней мономов по модулю $8$ ). Найти многочлен $v(t)$ можно методом неопределённых коэффициентов, но быстрее из следующего алгоритма:

2 8 2 4 4 8 8 x (t)= 1+t+ t = t, x (t)= t,x (t)= t= 1

Следовательно,

7 3 4 4 2 4 2 6 7 v(t)= x (t)= x(t)x (t)= (1+t+ t)tt = t +t + t

Ответ:

$v =x2+ x6+ x7$

Ошибка.
Попробуйте повторить позже

Задача 5#68240

Пароли в системе составляются из букв английского алфавита (26 букв) и цифр. При этом требуется, чтобы в пароле содержались цифра и заглавная буква. Пользователь допускается в систему, если предъявленный им пароль отличается от установленного не более чем в одном символе. Сколько паролей, соответствующих требованиям составления, позволят войти в систему, если для пользователя был установлен пароль Tw38dttf (не совпадающих с установленным паролем)?

Источники: Верченко-2023 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Посмотрите, сколько способов есть заменить маленький символ в пароле? А цифру? А заглавную букву? И помните про условие, что обязательно должна быть заглавная буква и цифра)

Показать ответ и решение

Раскладываем пароль "по слоям": цифра + заглавная + строчная и смотрим, какие ограничения есть по замене в каждой позиции. Цифр две, поэтому одну из них можно заменить произвольно на любой знак из $26+ 26+ 10 − 1= 61$ . Если менять заглавную T, то только на заглавную: $26− 1= 25$ вариантов. Строчные можно на любые, это ещё $5⋅61= 305$ вариантов. Итого $2⋅61+ 25+5 ⋅61 =452$ вариантов.

Ответ: 452

Ошибка.
Попробуйте повторить позже

Задача 6#68239

На координатной плоскости в точках $A(2,4),B(8,8),C(8,0),D (14,1)$ и $E(8,1)$ расположены вышки сотовой связи. Будем говорить, что абонент находится в зоне действия данной вышки, если расстоянии до неё меньше, чем до любой другой вышки. Найдите площадь зоны действия вышки $E.$

Источники: Верченко-2023 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Для начала изобразим наши точки на координатной плоскости. Попробуйте подумать над двумя вышками, какая область будет под действием одной из них?

Подсказка 2

Можно посмотреть на отрезок между этими двумя вышками и просто посмотреть на серединный перпендикуляр к нему: это геометрическое место точек, такое что расстояние от одной и другой вышек одинаковые до них. И если сместиться в одну сторону - то ближе будет одна вышка, в другую - другая) Попробуйте применить серединные перпендикуляры для вышки E и всех остальных!

Показать ответ и решение

Для начала требуется отобразить точки на координатной плоскости. Так как по условию задачи требуется найти площадь зоны действия вышки $E$ , то соединим отрезками точку $E$ с точками $A,B,C,D$ . Далее проведём через полученные отрезки серединные перпендикуляры и выделим область, полученную пересечением таких перпендикуляров (отмечены на рис. оранжевым цветом). Таким образом, получаем трапецию (см. рисунок ниже), которая демонстрирует область зоны действия вышки $E$ :

$PIC$

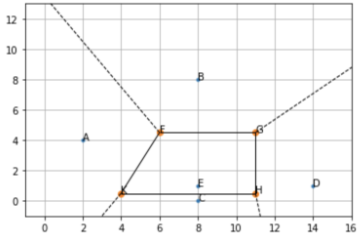
Осталось посчитать площадь полученной трапеции. Пересечение срединных перпендикуляров дало нам 4 точки с координатами $F(6,4.5),H (11,0.5),K(4,0.5),G(11,4.5)$ . Площадь данной трапеции

S = 12 ⋅(HK + FG)⋅HG = 12 ⋅(5+ 7)⋅4= 24

Ответ: 24

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#68238

Найдите все восьмизначные числа $A = aa-...a-, 12 8$ $a ∈ {1,2,...,9} i$ такие, что $8⋅A+ a = B, 8$ где $B =b-b-...b 12 8$ , $b = 10 − a . i i$ Решение обоснуйте.

Источники: Верченко-2023 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Мы понимаем, как устроены цифры B относительно цифр A. Какое выражение с использованием A и B можно составить, которое не будет зависеть от конкретных цифр в числе А?

Подсказка 2

A+B! А дальше просто решается задачка, нахождением последней цифры числа A)

Показать ответ и решение

Заметим, что $A+ B =11...10 = 108−1⋅10 ◟-◝8◜ ◞ 9$ . Тогда из условия $8⋅A +a = B 8$ получим $9A+ a = 11 ...10 8 ◟ ◝◜8-◞$ . Следовательно, $a = 8 8$ . Разделим число $1◟1.◝◜..1◞0− 8 8$ на $9$ . Получим число $12345678.$

Ответ: 12345678

Ошибка.
Попробуйте повторить позже

Задача 8#75003

Подписью битового сообщения $(a,...,a ) 1 5$ является любой битовый набор $(x ,...,x ), 1 10$ при котором

$pict$

Здесь $⊕$ — стандартная операция сложения битов: $0⊕ 0= 1⊕ 1= 0,0⊕ 1= 1⊕ 0= 1.$

Найдите какую-нибудь подпись для сообщения $(0,1,0,0,0).$

Источники: Верченко-2022 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Задача только запугивает большим числом переменных, но это же обычная система уравнений, которые мы умеем решать. Так давайте подставим наше сообщение в левую часть условия.

Подсказка 2

Мы понимаем, что складывая одинаковые переменные они уничтожаются, поэтому полезно поскладывать уравнения в этой системе, тем самым, упростив её.

Подсказка 4

Сложите первые 3 уравнения, используя полученные знания, сложите 4-ое и 5-ое уравнения.

Подсказка 5

Теперь мы можем перейти к настоящей пугающей части, но не спешим расстраиваться, ведь нам нужно найти какой-нибудь набор иксов, а значит мы можем дополнительно навесить на него удобные нам ограничения, и если получится найти набор с доп. ограничениями, то задача решена. Какие бы ограничения нам тогда наложить?

Подсказка 6

Давайте перейдём от квадратичной системы к линейной, зафиксировав значения (x7,x8,x9,x10)=(1,1,0,0), и попробуем решить систему попроще.

Подсказка 7

Не забываем, что помимо действий с уравнениями мы можем делать действия внутри уравнения, давайте избавимся от 1, добавив их к обеим частям. Посмотрите на уравнения 2,4 и 1,3, дальше уже можно найти решение и радоваться победе!

Показать ответ и решение

Для начала, используя $(a,a ,a ,a,a )= (0,1,0,0,0), 1 2 3 4 5$ найдем $b,b,b,b ,b . 1 2 3 4 5$ Для этого решим систему:

( b ⊕ b ⊕b = 0 ||||| 3 4 5 |{ b2⊕ b4⊕b5 = 1 ||| b2⊕ b3⊕b5 = 0 |||( b1⊕ b2⊕b3 = 0 b1⊕ b3⊕b5 = 0

Сложив первые три уравнения и преобразовав их, получаем $b = 1. 5$ Подставим это значение в нашу систему:

(| b ⊕ b =1 ||||| b3⊕ b4=0 { b2⊕ b4=1 |||| b2⊕ b3⊕b = 0 ||( 1 2 3 b1⊕ b3 =1

Сложим четвертое и пятое уравнения и получим, что $b2 = 1.$ Тогда из второго уравнения следует, что $b4 = 1,$ а из третьего следует, что $b3 = 0.$ Тогда из пятого получаем $b1 =1.$

Итак, $(b,b ,b ,b,b)= (1,1,0,1,1). 1 2 3 4 5$ Теперь нужно найти набор какой-нибудь $(x ,x,x ,x ,x ,x ,x,x ,x,x ). 1 2 3 4 5 6 7 8 9 10$

Для этого найдем любое решение системы:

(| x x ⊕ x x ⊕ x x ⊕x x ⊕ xx ⊕x x ⊕ xx ⊕ x x = 1 ||||| x1x9⊕ x21x0⊕x 3x 8⊕x4x9⊕ x5x9 ⊕ 6x 8x ⊕7x8x ⊕9x 10x = 1 { x1x8⊕ x29x ⊕ 3x 1x0⊕x4x8⊕ x5x10⊕x 6x10⊕ xx7⊕8x 8x 9⊕x = 0 |||| 1 9 210 3 8 4 7 58 6 8 7 8 8 9 10 ||( x1x7⊕ x2x10⊕ x3x10⊕ x4x7⊕x5x7⊕ x6x10⊕ x7x10⊕ x9x10 =1 x1x8⊕ x2x7 ⊕x3x7⊕ x4x9⊕ x5x9⊕x6x8⊕ x7x8 ⊕x8x10⊕x9 = 1

Решать квадратичную систему с десятью переменными сложно, поэтому попробуем ее как-нибудь упростить. Видно, что если убрать переменные $x ,x ,x ,x , 7 8 9 10$ то получится линейная система. Тогда зафиксируем значения этих переменных так, чтобы в новой системе не было противоречий, например, так: $(x7,x8,x9,x10)= (1,1,0,0).$ Тогда все слагаемые, в которых есть $x9$ или $x10$ пропадут.

После подстановки этих значений в систему получаем:

( ||||| x3⊕ x6 ⊕1= 1 |{ x1⊕ x4 ⊕1= 1 ||| x3⊕ x4 ⊕x5⊕ x6⊕ 1= 0 |||( x1⊕ x4 ⊕x5 = 1 x1⊕ x2 ⊕x3⊕ x6⊕ 1= 1

Далее во всех уравнениях, где есть слагаемое 1 в левой части, прибавим 1 к обеим частям. Тогда справа константа изменится на противоположную, а слева останутся только переменные.

( ||||| x3⊕ x6 = 0 |{ x1⊕ x4 = 0 ||| x3⊕ x4⊕ x5 ⊕x6 = 1 |||( x1⊕ x4⊕ x5 =1 x1⊕ x2⊕ x3 ⊕x6 = 0

Из второго и четвертого уравнений следует, что $x = 1. 5$ Тогда из первого и третьего получаем, что $x = 0. 4$ Теперь подставим эти значения в систему:

( x ⊕ x = 0 ||||| 3 6 |{ x1 = 0 ||| x3⊕ x6 = 0 |||( x1 = 0 x1⊕ x2⊕ x3 ⊕x6 = 0

Итак, $x1 = 0.$ Тогда из первого и пятого получаем, что и $x2 =0.$ Осталось выбрать какие-нибудь значения для $x3x6,$ так как их система однозначно не задает. Пусть $x = x = 0. 3 6$

Получаем следующую подпись: $(0,0,0,0,1,0,1,1,0,0).$

Ответ:

$(0,0,0,0,1,0,1,1,0,0)$

Ошибка.
Попробуйте повторить позже

Задача 9#71371

В Криптоландии используется алфавит, состоящий из четырёх латинских букв $a,b,c,d.$ Любая последовательность букв алфавита будет словом криптоландского языка при выполнении единственного ограничения: если в последовательности есть хоть одна буква " $a$ то тогда в ней обязательно должны встретиться две буквы " $a$ "подряд.

Например, последовательности $baacda,aabb,ddd$ являются словами, а последовательности $bcadda,abba$ — не являются. Найдите число слов длины 8 в криптоландском языке.

Источники: Верченко-2022 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Всего существует 4⁸ последовательностей длины 8, составленных из букв криптоландского алфавита. Подумайте, как удобнее всего почитать число тех последовательностей, которые являются словами.

Подсказка 2

Все последовательности разбиваются на три непересекающихся множества: 1. Не содержащие буквы a; 2. Содержащие букву а и хотя бы одну пару аа; 3. Содержащие букву а и не содержащие ни одной пары аа. При этом очевидно, что элементы 1 и 2 множеств являются словами, а 3 - нет. Посчитать число элементов второго множества выглядит либо очень сложной задачей, либо вовсе нереальной. Тогда удобнее всего найти число последовательностей, являющихся словами, будет просто вычтя из 4⁸ число элементов 3 множества. Подумайте, каким образом их можно сосчитать.

Подсказка 3

Для n букв а в слове возможно найти число способов расставить их в последовательности длины 8 по формуле: число сочетаний из 8+1-n по n. Кроме того у нас есть еще 3^(8-n) способов расставить b, c, d на оставшиеся места. Подумайте, какое максимально значение может принимать n.

Подсказка 4

При n ≥ 5 гарантировано будет существовать пара aa. Значит, они нам не подходят. Теперь найдем число последовательностей для n = 1, 2, 3, 4, сложим их и таким образом получим количество элементов 3 множества.

Показать ответ и решение

Множество всех последовательностей длины $8$ состоит из $48$ последовательностей. Это множество разбивается на три непересекающихся между собой подмножества:

1.: Последовательностей, не содержащих $a.$
2.: Последовательностей, содержащих $a,$ но не содержащих двух подряд идущих таких букв.
3.: Последовательностей, содержащих $a$ , в которых встречаются две подряд идущие такие буквы.

Чтобы решить задачу, нужно найти число последовательностей во втором подмножестве и вычесть его из числа $48.$

В свою очередь, множество последовательностей второго типа можно разбить на непересекающиеся подмножества, в которые входят последовательности, содержащие $1,2,3,4$ букв " $a$ ".

Поскольку число последовательностей длины $8$ , содержащих ровно $t$ отдельно стоящих букв $a$ , равно $Ct8+1−t(4− 1)8−t,$ то общее число последовательностей второго типа будет равно

4∑ t 8−t C9−t3 =38070 t=1

В итоге получаем

48 − 38070 =27466

Ответ: 27466

Ошибка.
Попробуйте повторить позже

Задача 10#71370

Знаками открытого и шифрованного текстов являются пары целых от 0 до 31. Для зашифрования используется секретный ключ $k$ (целое число от 0 до 31), заданная таблично функция $h,$ а также функция $g(c,d),$ которая паре целых чисел $(c,d)$ ставит в соответствие пару $(d,c+ h(d+k))$ (причем если число $d +k$ или $d+ h(d+ k)$ превышает 31 , то их заменяют остатком от деления на 32 $).$ Знак шифрованного текста $(b1,b2)$ получается из знака открытого текста $(a1,a2)$ путем 128-кратного применения функции $g :$

(b1,b2)= g128(a1,a2)= g(...g(g(a1,a2)))

Известно, что знак открытого текста $(21,0)$ преобразовался в знак зашифрованного текста $(15,25),$ знак $(7,3)$ преобразовался в $(29,5),(0,17)$ — в $(25,4)$ и, наконец, $(5,21)−$ в $(22,9).$ Найдите ключ $k.$


$i$	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20

$h(i)$	9	1	30	4	24	12	8	23	18	7	16	15	21	26	10	17	19	22	13	28	14


21	22	23	24	25	26	27	28	29	30	31

11	2	29	3	6	27	0	5	25	31	20

Источники: Верченко-2022 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Применять 128 раз одну и ту же функцию очень сложно...поэтому было бы хорошо, если мы сразу могли понимать, а что у нас получается на каждой итерации? Может ли в итоге у двух разных пар получиться один и тот же знак?

Подсказка 2

Если две пары отличаются одним применением функции, то и их знаки тоже отличаются одним применением функции. Как это связать с условием?

Подсказка 3

Попробуем найти такие пары чисел, которые удовлетворяют утверждению из подсказки 2. Теперь мы знаем, какие пары отличаются применением функции g! Несложно найти k)

Показать ответ и решение

Необходимо заметить, что из равенств

128 (b1,b2)= g (a1,a2)

( ′ ′) 128( ′ ′) b1,b2 = g a1,a2

(a′,a′)= g(a,a ) 1 2 1 2

следует равенство

(b′,b′)= g(b,b ) 1 2 1 2

Необходимым условием выполнения равенств $(a′1,a′2)= g(a1,a2),(b′1,b′2)= g(b1,b2)$ являются равенства $a′1 = a2,b′1 = b2.$ Среди приведенных в задаче пар знаков открытого и шифрованного текстов есть знаки, удовлетворяющие этому условию: одна пара $(21,0),(0,17)$ и вторая пара $(29,5),(5,21).$ То есть

(15,25)=g128(21,0)

(25,4)= g128(0,17)

Из условия задачи возможность найти ключ — воспользоваться равенствами

(0,17)= g(21,0), (25,4)= g(15,25)

Убедимся, что при этих условиях оба равенства дают одинаковое значение ключа $k.$

$PIC$

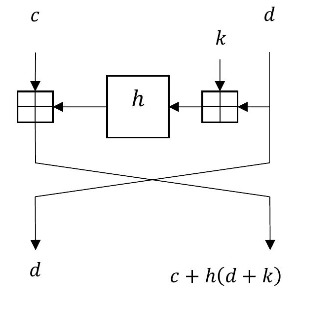
Получаем, что $k= 19.$

Ответ: 19

Ошибка.
Попробуйте повторить позже

Задача 11#71013

На вход устройства подается лента с записанными на ней нулями и единицами:

$PIC$

За один такт устройство считывает с ленты с позиций $μ1,μ2,μ3$ (на первом такте $μ1 = 1$ ) три значения $x,y,z$ . Если $x+ y+z ≥2,$ то устройство на новой ленте печатает 1 , иначе — 0 . Затем устройство сдвигается на одну позицию вправо, и процедура повторяется. Найдите разности $d1 = μ2− μ1$ и $d2 = μ3− μ2,$ если известно, что $d1 +d2 ≤ 10,$ а на новой ленте было напечатано следующее: $0001000010111111000111010111011010101001 ...$ (для примера на рисунке изображен случай $d1 = 3,d2 =5).$

Источники: Верченко-2022 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Да, можно и перебрать d_1 и d_2, но это будет долго) Попробуем сократить перебор! Что мы вообще умеем делать? Мы умеем брать конкретные элементы ленты и считать их сумму, если расстояния между ними это d_1 и d_2. Какие "удобные" элементы хочется взять?

Подсказка 2

Рассмотрим систему неравенств, которая соответствует выходных знакам вида 1...1 на расстоянии d_1. С помощью нее мы сможем дать ограничения на элементы, находящиеся на расстоянии d_1. Таким образом мы сможем перебрать и методом "пристального взгляда на ленту" найти d_1. Аналогично с d_2!

Показать ответ и решение

Число возможных вариантов $d 1$ и $d :10+ 9+ ⋅⋅⋅+1 =55 2$ , можно для каждого варианта проверять, что соответствие входных и выходных символов, а можно предложить более быстрый способ, заключающийся в нахождении сначала $d1$ (максимум 10 вариантов), а затем $d2$ . Для этого достаточно заметить следующее.

Если рассмотреть систему, соответствующую выходным знакам на расстоянии $d1$ вида $1...1$ в произвольном такте работы $μ1 :$

xμ1 + xμ1+d1 − xμ1+d1+d2 ≥ 1,

xμ1+d1 +xμ1+2d1 − xμ1+2d1+d2 ≥ 1,

то если $x = 0 μ1+d1$ , то $x = 1,x = 1. μ1 μ1+2d1$

Это позволяет отбраковать опробуемый вариант $d . 1$ Устанавливаем, что $d = 2. 1$

Аналогично, если рассмотреть систему, соответствующую выходным знакам на расстоянии $d2$ вида $0...1$ в произвольном такте работы $μ1 :$

xμ1 + xμ1+d1 − xμ1+d1+d2 ≤ 0,

xμ1+d2 +xμ1+d1+d2 − xμ1+d1+2d2 ≥1,

тогда если $xμ1+d1+d2 = 0,$ то $xμ1+d1 = 0,xμ1+d1+2d2 = 0.$

Это позволяет отбраковать опробуемый вариант $d 2$ (с учётом найденного ранее $d =2). 1$ Находим $d = 6. 2$

Ответ:

$d = 2,d =6 1 2$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#71012

Петя использует для работы в интернете пароли из шести символов. Опасаясь злоумышленников, он решил в каждом пароле изменить порядок следования символов, используя для этого одно и то же правило, которое записал в книжечку. Правило могло выглядеть, например, так:

( ) 1 2 3 4 5 6 3 6 4 5 1 2

То есть первый символ ставится на третье место, второй - на шестое и так далее. В своем пароле для почты qwerty Петя переставил буквы по правилу из книжечки, а затем, для большей надежности переставил буквы по этому же правилу еще раз. (Если использовать правило как в примере, то из qwerty после первой перестановки получится tyqerw, а после второй — rwtqey).

a) Какие из нижеследующих комбинаций


yetrqw	eyrtqw	yrwteq	rewqyt	qwtyre	tywreq

могли быть получены двойной перестановкой букв в пароле qwerty? (используя, возможно, другие правила указанного вида)

б) Петя потерял книжечку! Он помнит, что первоначально пароль был qwerty, но правило, по которому были в нём дважды переставлены буквы, не помнит. За какое наименьшее число попыток можно с гарантией подобрать утерянный пароль?

Источники: Верченко-2022 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

В этой задачи нам описали какой-то алгоритм и просят понять, что могло быть результатом этого алгоритма. В таких задачах полезно поискать инварианты (то, что не меняется в результате работы алгоритма) или свойства: как данный алгоритм работает для некоторых схожих входных данных. Обратите внимание на то, что в алгоритме как бы описаны взаимодействия между объектами: символ с места A переходит в символ с местов B, а какой математический объект позволяет нам показывать связи между объектами?

Подсказка 2

Правильно, можно использовать граф, попробуйте нарисовать его для правила из "примера", а затем для двойной перестановки и посмотрите, как он изменился. Если не сразу понятно, на что обращать внимание, то придумайте своё правило для перестановки чисел и проделайте те же действия.

Подсказка 3

Можно заметить, что циклы длины 2n распадаются на 2 цикла длины n, а каждый цикл длины 2n+1 остаётся длины 2n+1 (взаимосвязи между объектами другие, но длина та же). Ага! Из каждого объекта при какой-то операции получается по 2 объекта, на что это похоже?

Подсказка 4

Попробуйте сформулировать аналог леммы о рукопожатиях (граф имеет чётное число вершин нечётных степеней), но для циклов, подумайте для циклов какой длины утверждение становится более сильным, а для какой не несёт никакой информации, из циклов какой длины можно получить циклы другой длины?

Подсказка 5

Верно, если мы посмотрим, что происходит с циклами длины 2 * (2n+1) (длина которых делится на 2, но не делится на 4), то они просто превращаются в нечётные циклы, а так как мы не знаем, сколько изначально было циклов нечётной длины, то про их итоговую чётность мы ничего сказать не можем. Почему бы тогда не посмотреть на циклы чётной длины, ведь они могут получиться только из циклов кратных 4. А сколько тогда циклов чётной длины будет?

Подсказка 6

Да, циклов чётной длины чётное количество, иначе бы не выполнялось утверждение о том, что из циклов длины 2n получаются 2 цикла длины n. Осталось посмотреть, какие из перестановок из пункта "а" противоречат данному утверждению, а для остальных найти пример!

Подсказка 7

Давайте сразу определимся, что "за n попыток можно с гарантией подобрать пароль" значит, что какие бы случайные n попыток мы не сделали, хотя бы одна из них даст нам наш пароль. Понятно, что тогда надо посчитать общее количество двойных перестановок, оно и будет ответом. Остаётся только понять, что на самом деле мы доказали критерий существования двойных перестановок (Двойная перестановка существует тогда и только тогда, когда циклов чётной длины чётное количество, попробуйте показать, почему это работает и в обратную сторону).

Подсказка 8

Попробуйте разбить подсчёт на более простые случаи. Если всего 6 элементов в графе, то сколько циклов и какой длины может быть при условии, что это двойная перестановка? Всегда при подсчёте задавайте себе вопросы: а важен ли порядок? А есть ли граничные случаи и все ли их я рассмотрел?

Показать ответ и решение

Приведенное в условии правило перестановки букв, или перестановку, будем обозначать греческой буквой $σ.$ Перестановку $σ$ можно интерпретировать как отображение множества цифр ${1,2,3,4,5,6}$ в себя. Например, тот факт, что первая буква перешла на третье место, можно записать как $σ(1)= 3,$ а также изобразить стрелочкой из 1 в 3:

$PIC$

Видно, что если бы мы перестановку $σ$ применяли многократно, то буквы на 2-й и 6-й позициях постоянно менялись бы местами, а буквы на позициях 1, 3, 4, 5 переставлялись бы по циклу. Поэтому перестановка $σ$ может символически быть записана в виде произведения циклов:

( ) σ = 1 2 3 4 5 6 = (1345)(26)= 4∗2 3 6 4 5 1 2

Запись $4∗ 2$ отражает цикловую структуру перестановки $σ,$ показывая, что в ней один цикл длины 4 и один цикл длины 2.

Посмотрим теперь более детально на то, что произойдет, если по правилу $σ$ переставить буквы еще раз. Так 1 при первом применении правила $σ$ перешла в 3: $σ(1)=3,$ а при повторном применении 3 перешла в 4: $σ(3)= 4.$ Значит, в результате двойной перестановки 1 переходит в 4. Будем это записывать как $σ(σ(1))= 4$ или же $2 σ (1) =4.$ Поэтому правило двойной перестановки букв, представляющее собой квадрат перестановки $σ,$ выглядит так:

$PIC$

Заметим, что после повторной перестановки 2 и 6 вернутся на свои места, то есть цикл $(2,6)$ распадется на два тривиальных цикла $(2)$ и $(6),$ а цикл $(1345)$ превратится в два цикла $(1,4)$ и $(3,5).$ Таким образом, при повторном применении перестановки циклы четной длины $2n$ распадаются на два цикла, длины $n$ каждый. Несложно проверить, что при этом циклы нечетной длины сохраняются. Справедливо утверждение.

Утверждение. Перестановка представляет собой полный квадрат в том и только том случае, когда в ее представлении в виде произведения непересекающихся циклов может быть сколько угодно и какие угодно циклы нечётной длины, в то время как циклов одной и той же чётной длины должно быть чётное число.

Рассмотрим первую комбинацию уеqwrt из пункта а). Она получена из qwerty перестановкой $( ) 1 2 3 4 5 6 = (1324561), 3 4 2 5 6 1$ которая представляет собой цикл длины 6. Поскольку циклов четной длины здесь нечетное количество (всего один), то, согласно утверждению, такая комбинация двойной перестановкой букв получиться не могла. Аналогично исследуются и остальные комбинации в пункте а).

Проведем подсчет общего числа перестановок, являющихся полными квадратами. Их цикловые структуры могут быть следующие:

$1∗ 1∗1∗1∗ 1∗1.$ Это перестановка, оставляющая все на своих местах (тождественная перестановка). Она единственна.
$1∗ 5.$ Мы должны выбрать 5 элементов из шести, чтобы составить цикл дины 5. Это можно сделать 6-ю способами. Из пяти элементов цикл длины 5 можно организовать $(5− 1)!$ способами (действительно, организуем цикл из пяти элементов $a1,a2,a3,a4,a5;$ элемент $a1$ может перейти в любой из четырех (т.к. в себя нельзя), элемент $a2$ переходит в один из оставшихся трех и т.д. В итоге получаем $4 ⋅3 ⋅2 ⋅1$ способов). Таким образом, здесь $6⋅4!= 144$ перестановок.
$2∗ 2∗1∗1.$ Выбрать два элемента из шести для первого цикла длины 2 можно $2 C6$ способами. Для второго цикла длины 2 есть $2 C4$ способа. Итого $2 2 C 6 ⋅C4 = 90.$ От порядка следования циклов результат не зависит, поэтому 90 еще следует разделить на два. Всего 45 перестановок с такой структурой.
$3∗ 3.$ Здесь мы 6 элементов десятью способами $( ) 12C36 = 10$ разбиваем на две тройки и из каждой тройки получаем по 2 цикла. Всего 40 перестановок.
$3∗ 1∗1∗1.$ Здесь мы двадцатью способами $( ) C36 = 20$ выбираем тройку и из каждой тройки получаем по 2 цикла. Всего 40 перестановок.