Стереометрия на ДВИ —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Стереометрия на ДВИ

Тема ДВИ по математике в МГУ

Стереометрия на ДВИ

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела дви по математике в мгу

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#64686

Дан куб $ABCDA ′B′C′D ′.$ Через середины его ребер $AA′,C′D ′$ и через центр грани $BCC ′B′$ проведена плоскость, пересекающая диагональ $′ DB$ куба в точке $O$ . Найдите отношение $DO$ : $′ OB .$

Подсказки к задаче

Подсказка 1

Построение этого сечения не выглядит тривиальной задачей. Разберёмся для начала, какие точки этой плоскости нам нужны, чтобы отыскать искомое соотношение. Удобно будет работать с пересечением этой плоскости (назовем ее π) и диагональной (BDD'). Значит нам точно понадобится пересечение π c рёбрами BB' и DD'.

Подсказка 2

Можно заметить, что середина ребра C'D' и центр грани BCC'B' лежат в плоскости диагонального сечения (ABC'). Рассмотрите эту плоскость и поработайте с подобными треугольниками, чтобы определить точку пересечения плоскости π с прямой АВ — зная её, мы сможем посчитать и положение точки пересечения π с ребром BB'.

Подсказка 3

Определить точку пересечения π и DD' тоже не получится в один шаг: удобно это сделать сначала рассматривая всё ту же плоскость (ABC') и прямую AD' в ней. А потом можно будет высчитать и положение точки на DD'.

Подсказка 4

Осталось рассмотреть плоскость (BDD') и имеющуюся у нас теперь прямую её пересечения с π. Поработайте с подобными треугольниками, чтобы отыскать то самое соотношение DO:OB'

Показать ответ и решение

$PIC$

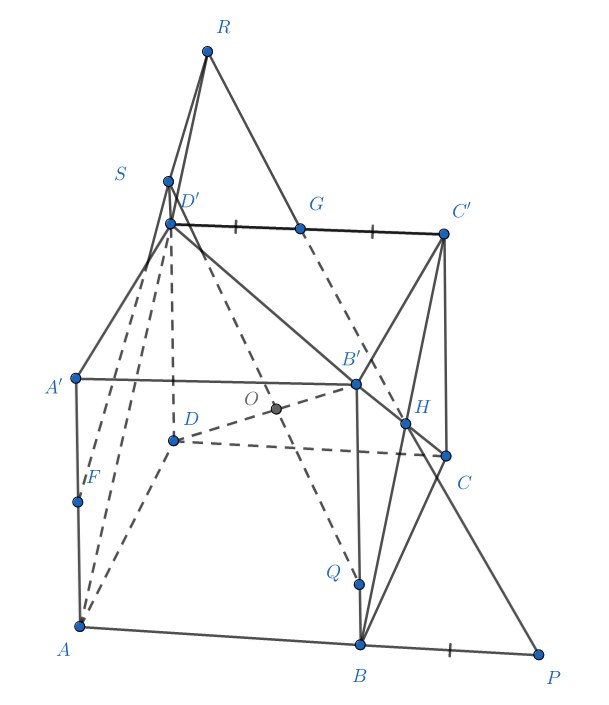
Обозначим середины ребер $AA′,C′D ′$ и центр грани $BCC ′B′$ через $F,G,H$ , соответственно. Обозначим также через $π$ плоскость $FGH$ .

Найдем точку $Q$ пересечения плоскости $π$ и прямой $BB′$ . Точки $G,H,A,B$ лежат в плоскости $ABC ′$ , следовательно прямые $GH$ и $AB$ пересекаются. Пусть $P$ - точка их пересечения. Тогда $BP = C′G= 12AB$ , поскольку треугольники $HC′G$ и $HBP$ равны. Точки $P$ и $F$ принадлежат $π$ , следовательно, прямая $FP$ есть прямая пересечения плоскости $ABB ′$ с $π$ . То есть $Q$ лежит на отрезке $BB ′$ . Из подобия треугольников $APF$ и $BPQ$ следует, что $BQ = 13AF = 16BB ′$ . Следовательно, $QB ′ = 56BB′$ .

Найдем теперь точку $S$ пересечения плоскости $π$ и прямой $DD ′$ . Прямая $GH$ лежит в плоскости $ABC ′$ , равно как и прямая $AD′$ . Обозначим через $R$ точку пересечения этих прямых. Из подобия треугольников $RAP$ и $RD ′G$ следует, что $RD ′ = 13RA$ . Точки $R$ и $F$ принадлежат $π$ , следовательно, прямая $F R$ есть прямая пересечения плоскости $ADD ′$ с $π$ . То есть $S$ лежит на продолжении отрезка $DD ′$ за точку $D ′$ . Из подобия треугольников $ARF$ и $D′RS$ следует, что $D′S = 1AF = 1DD ′ 3 6$ . Следовательно, $SD = 7DD ′ 6$ .

Прямая $SQ$ есть прямая пересечения плоскости $DBB ′$ с $π$ , то есть она проходит через $O$ . Треугольники $SDO$ и $QB′O$ подобны с коэффициентом подобия $7 5$ . Следовательно, $DO :OB′ =$ $7:5$ .

Ответ:

$7 5$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#64685

Дана правильная треугольная пирамида $ABCS$ с основанием $ABC$ и вершиной $S.$ Плоскость $π$ перпендикулярна ребру $AS$ и пересекает рёбра $AS,BS$ в точках $D,E$ соответственно. Известно, что $SD = AD$ и $SE = 2BE.$ Найдите косинус угла между ребром $AS$ и плоскостью основания $ABC.$

Подсказки к задаче

Подсказка 1

Пирамида правильная, поэтому мы чётко знаем куда падает её высота и искомый косинус будет легко выражаться, как только мы узнаем отношение её бокового ребра к ребру основания. Плоскость π перпендикулярна AS. Что в таком случае можно сказать о прямой DE пересечения этой плоскости с плоскостью (SAB)?

Подсказка 2

Итак, DE ⊥ AS. Тогда мы можем, зная положения точек D и E выразить косинус угла при вершине S. Рассмотрите теперь равнобедренный треугольник-грань △ASB: теорема косинусов поможет нам связать его боковые стороны со стороной основания.

Подсказка 3

Пирамида правильная, значит её высота падает в центр основания. Воспользуйтесь свойствами правильного треугольника и найденным в предыдущем пункте соотношением, чтобы выразить искомый косинус.

Показать ответ и решение

$PIC$

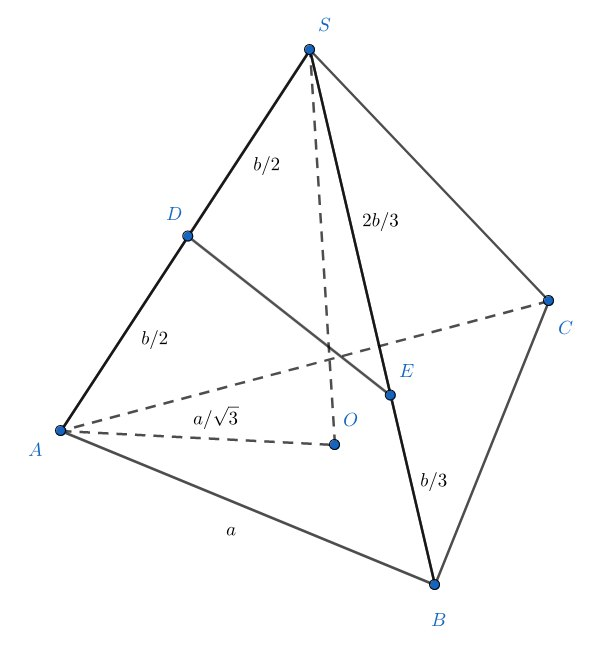
Пусть $a$ — длина ребра основания и $b$ — длина бокового ребра. В прямоугольном треугольнике $SDE$ имеем $SD = 12b$ и $SE = 23b$ . Стало быть, $cos∠ASB = 34$ . Применяя теорему косинусов к треугольнику $ASB$ , получаем, что $a2 =2b2− 2b2⋅ 34$ , откуда $√- b= a 2$ . Пусть $O$ — центр основания. Тогда в прямоугольном треугольнике $ASO$ имеем $√ - AS = b=a 2$ и $√- AO =a∕ 3$ . Стало быть, $√- cos∠SAO = AO∕AS =1∕ 6$ .

Ответ:

$√1- 6$

Ошибка.
Попробуйте повторить позже

Задача 3#64684

Высота правильной треугольной призмы $ABCA ′B′C′$ с основанием $ABC$ и боковыми рёбрами $AA ′,BB ′,CC′$ равна $1.$ Найдите длину ребра основания, если известно, что $′ ′ AB ⊥ BC .$

Подсказки к задаче

Подсказка 1

Как мы можем применить данную нам перпендикулярность? Кажется, будет удобно построить из точки B' прямую B'B₁, параллельную BC' и взглянуть, на полученную конструкцию. Обозначьте неизвестную сторону основания какой-нибудь переменной и попробуйте выразить всё что тут можно!

Подсказка 2

В основании правильный треугольник, значит у нас есть угол в 60°. Имея в треугольнике две стороны и угол мы сумеем выразить третью сторону: отрезок, соединяющий А с точкой пересечения B'B₁ и плоскости основания. Эту же сторону мы можем выразить при помощи т. Пифагора.

Подсказка 3

Осталось только решить квадратное уравнение, отсечь лишний корень (сторона ведь не может быть отрицательной!) и задача повержена!

Показать ответ и решение

$PIC$

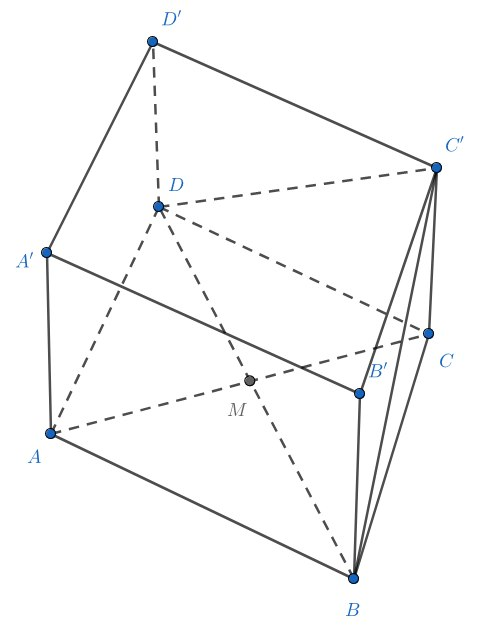
Достроим основания призмы $ABC, A′B ′C ′$ до параллелограммов, получим $ABCD,A ′B′C′D′$ . Получится параллелепипед, в котором $AB ∥DC, AB =CD$ и $AB ′ ∥DC′,AB′ = DC′$ , отсюда $DC′ ⊥ BC ′$ . Кроме того, $BC′ = DC′$ (призма правильная, можно воспользоваться симметрией. Отсюда $△BC ′D$ прямоугольный и равнобедренный. Если $AC ∩ BD = M$ , то $C ′M$ будет высотой этого треугольника, если дополнительно $AB = a$ , то $√- C′M =DM =BM = -32a,CM = AM = a2$ (используем свойства правильного треугольника). Из условия $CC ′ =1$ , применяя теорему Пифагора: $- C′C2+ CM2 = C′M2 ⇐ ⇒ 1+ a2∕4= 3a2∕4 ⇐⇒ a= √2$ .

Ответ:

$√2$

Ошибка.
Попробуйте повторить позже

Задача 4#63819

Сфера касается всех рёбер тетраэдра $ABCD$ . Известно, что произведения длин скрещивающихся рёбер равны. Известно также, что $AB = 3,BC = 1$ . Найдите $AC.$

Подсказки к задаче

Подсказка 1

Подумаем, как можно применить условие о том, что сфера касается всех рёбер тетраэдра? Более всего с длинами рёбер тут связывается свойство касательных: отрезки касательных к сфере, проведенных из одной точки, равны! Обозначьте одной буквой все равные отрезки проведённые из каждой из вершин и при помощи этих букв запишите равенство произведений длин скрещивающихся рёбер. ---

Подсказка 2

Поработайте теперь с нашим двойным равенством: рассмотрите две пары уравнений и попробуйте их преобразовать. Какие интересности связанные с отрезками касательных из разных вершин можно заметить?

Подсказка 3

Если сделать всё аккуратно, то получится несколько вариантов: равны либо отрезки касательных проведённые из вершин А и С, либо проведённые из вершин В и D. Рассмотрите оба случая, не выходит ли в одном из них противоречий с условием задачи? (Не зря же нам даны AB и BC). Аналогично рассмотрите вторую пару вершин, отрезки касательных из которых равны. Останется лишь внимательная арифметика и АС откроется нам!

Показать ответ и решение

Расстояния от вершины $A$ до точек касания сферы с рёбрами $AB,AC,AD$ равны. Обозначим это расстояние $a$ . Соответствующие расстояния от вершин $B,C,D$ обозначим $b,c$ , $d$ соответственно. По условию $(a+ b)(c+ d)=(a+ c)(b+d)= (a+ d)(b+c)$ , что равносильно после раскрытия скобок системе

(a− c)(b− d)= 0 и (a − b)(c− d)= 0.

Если $a= c$ , то $AB =BC$ , а это не так. Значит, $b= d$ . Тогда либо $a= b$ , либо $c =b$ . Если $a =b$ , то $AC = BC = 1$ , что противоречит неравенству треугольника. Значит, $c=b$ и, стало быть, $AC =AB = 3.$

Замечание.

Тетраэдр, у которого произведения длин скрещивающихся рёбер равны, называется каркасным, можете поизучать его свойства. В задаче по сути просили доказать, что у такого тетраэдра суммы длин скрещивающихся рёбер равны.

Ответ:

$3$

Ошибка.
Попробуйте повторить позже

Задача 5#63818

Вписанная в треугольную пирамиду $ABCD$ сфера касается граней $BCD, ACD,ABD$ и $ABC$ в точках $A ,B ,C 1 1 1$ и $D 1$ соответственно. Известно, что $D1$ является точкой пересечения высот треугольника $ABC$ , что плоскости $ABC$ и $A1B1C1$ параллельны и что радиус окружности, описанной около треугольника $ABC$ в четыре раза больше радиуса окружности, описанной около треугольника $A1B1C1$ . Найдите отношение, в котором сфера делит отрезок $DD1$ , считая от вершины $D.$

Показать ответ и решение

Пусть $O −$ центр сферы и пусть $A ,B ,C − 2 2 2$ основания высот треугольника $ABC$ , опущенных из вершин $A,B,C$ соответственно. Рассмотрим четырёхугольники $OA1A2D1$ , $OB1B2D1, OC1C2D1$ . Каждый из них состоит из двух равных прямоугольных треугольников. При этом катеты $OD1,OA1,OB1,OC1$ равны.

Из равенства расстояний от $A1,B1,C1$ до плоскости $ABC$ следует, что равны углы $D1OA1,D1OB1,D1OC1$ , а стало быть, равны и углы $D1A2A1$ , $D1B2B1,D1C2C1$ . Значит, равны отрезки $D1A2,D1B2,D1C2$ , то есть $D1$ является точкой пересечения биссектрис треугольника $ABC$ . При этом $D1$ это ортоцентр $ABC$ . Стало быть, треугольник $ABC$ правильный. Поскольку углы $D1A2A1,D1B2B1,D1C2C1$ равны, $DD1 −$ высота пирамиды. Опустим из $A1$ перпендикуляр $A1D2$ на $DD1$ . Тогда радиус окружности, описанной около треугольника $A1B1C1$ равен $A1D2$ . Радиус же окружности, описанной около треугольника $ABC$ равен $AD1$ . Получаем, что $1 1 A2D1 = 2AD1 = 2 ⋅4A1D2 = 2A1D2$ . Отсюда видим, что $∘ ∠D1A2A1 = 60$ . Стало быть, $√- √- √- DD1 = 3⋅A2D1 = 3⋅ 3⋅OD1 = 3OD1$ . Получаем, что искомое отношение равно $(DD1 − 2OD1 ):2OD1 = 1:2.$

Ответ:

$1 :2$

Ошибка.
Попробуйте повторить позже

Задача 6#63816

Дан параллелепипед $ABCDA ′B′C′D′$ с основаниями $ABCD, A ′B′C′D′$ и боковыми рёбрами $AA ′,BB′,CC′,DD ′$ . Все рёбра параллелепипеда равны. Плоские углы при вершине $B$ также равны. Известно, что центр сферы, описанной около тетраэдра $′ ′ AB CD$ , лежит в плоскости $′ AB C$ . Радиус этой сферы равен 2. Найдите длину ребра параллелепипеда.

Показать ответ и решение

Грани параллелепипеда являются ромбами. Поскольку плоские углы при вершине $B$ равны, равны также и плоские углы при вершине $′ D$ . Стало быть, $′ ′ ′ ′ AD = B D = CD$ как равные диагонали ромбов и, по той же причине, $′ ′ AB = BC = AC$ . Таким образом, центр сферы, описанной около тетраэдра $′ ′ AB CD$ , является центром окружности, описанной около правильного треугольника $′ AB C$ , а также является основанием высоты тетраэдра, опущенной из вершины $′ D$ . Отсюда получаем $′ √ - ′ √ - AB =2 3,AD =2 2$ . Итак, диагонали ромба равны $√ - 2 3$ и $√ - 2 2$ , значит, его сторона равна $√ - 5.$

Ответ:

$√5$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#63815

Дан тетраэдр $ABCD$ . Известно, что центр сферы, описанной около этого тетраэдра, лежит на $AB$ , что плоскости $ABC$ и $ABD$ перпендикулярны и что $AD =DC = CB$ . Найдите угол между прямыми $AD$ и $CB.$

Показать ответ и решение

Сразу отметим, что, поскольку центр сферы, описанной около тетраэдра, лежит на $AB$ , углы $ACB$ и $ADB$ - прямые. Далее, опустим перпендикуляры $CK$ и $CL$ на $AB$ и $BD$ соответственно. Тогда $DL = LB$ , ибо $DC = CB$ , следовательно, $KL −$ серединный перпендикуляр к $BD$ в плоскости $ABD$ и, поскольку $∘ ∠ADB = 90$ , точка $K$ является серединой $AB$ . Значит, $AC =BC$ . Аналогично, $AD = BD.$

Итак, $AC = BC = AD =BD =CD, AB ⊥CK, AB ⊥DK, AK = BK = CK =DK$ . Пусть $E −$ точка, симметричная точке $C$ относительно $K$ . Тогда $AK ⊥ EK ⊥ DK$ и $AK = EK =DK$ . Следовательно, треугольник $ADE −$ равносторонний. При этом $AE ∥CB$ . Стало быть, искомый угол равен углу $EAD$ и равен $∘ 60.$

Ответ:

$60∘$

Ошибка.
Попробуйте повторить позже

Задача 8#63889

Дан тетраэдр $ABCD$ . Известно, что $AB = BC =CD = 5$ и $CA = AD =DB = 6$ . Найдите косинус угла между рёбрами $BC$ и $AD.$

Подсказки к задаче

Подсказка 1

Какие способы поиска угла между скрещивающимися прямыми нам в принципе известны? В первую очередь хочется подумать о проведении прямой параллельной одной из них через точку на второй прямой. Будем рассматривать плоскость, проходящую через BC параллельно AD.

Подсказка 2

Чтобы построить искомый угол, ортогонально спроецируем точку А на построенную плоскость. Пусть получена точка А'. Рассмотрим отрезок MN, где N — cередина AD, M — середина ВС. Данных нам равенств отрезков достаточно, чтобы доказать, что он является общим перпендикуляром прямых AD и BC. Тогда какой угол будет искомым?)

Подсказка 3

Искомый угол ∠A'MB. Знание об общем перпендикуляре сразу же помогает нам найти А'М. Но чего-то ещё не хватает... Попробуем построить тут прямоугольный треугольник, чтобы легче было выражать угол! АА' перпендикуляр. Проведём из точки А наклонную АН такую что, точка Н лежит на ВС и АН ⊥ ВС. Тогда теорема о трёх перпендикулярах поможет нам увидеть △А'НМ с прямым углом Н, известной гипотенузой А'М и острым углом, чей косинус так хочется узнать!

Подсказка 4

Наклонная АН будет по сути высотой в треугольнике △АВС. При всех известных сторонах нетрудной найти АН и ВН. Отсюда один шаг до катета МН. Подставьте все нужные длины и получите косинус искомого угла!

Показать ответ и решение

Рассмотрим треугольник $ABC$ . Высота, опущенная из вершины $B$ , равна 4 , следовательно, высота $AH$ , опущенная из вершины $A$ , равна 24/5. Отсюда получаем $CH = 18∕5$ , $BH = 7∕5$ . Пусть $M$ - середина $BC$ . Тогда $MH = 5∕2− 7∕5= 11∕10.$

Пусть $N$ - середина $AD$ . Тогда $BN =CN$ и, стало быть, $MN ⊥ BC$ . Аналогично, $MN ⊥$ $AD$ . Рассмотрим плоскость, содержащую $BC$ и параллельную $AD$ . Спроецируем ортогонально на эту плоскость точки $A$ и $D$ . Полученные точки обозначим $′ A$ и $′ D$ . Точка $N$ при этом проецируется в точку $M$ . Стало быть, искомый угол равен $′ ∠A MB$ . Из прямоугольного треугольника $′ A MH$ получаем

MH MH 11 cos∠A′MB = cos∠A′MH = A′M--= AD∕2 = 30.

Ответ:

$11 30$

Ошибка.
Попробуйте повторить позже

Задача 9#63817

В основании четырёхугольной пирамиды $ABCDS$ лежит параллелограмм $ABCD$ . На ребре $SB$ отмечена точка $E$ , так что $SE :EB = 2:1$ . На ребре $SD$ отмечена точка $F$ , так что $SF :FD = 1:2$ . Найдите отношение, в котором плоскость $AEF$ делит объём пирамиды.

Показать ответ и решение

Проведём через точки $B,C,D$ соответственно прямые $l ,l ,l B C D$ , параллельные $AS$ . Обозначим через $B′,C′,D′$ соответственно точки пересечения плоскости $AEF$ с прямыми $lB,lC$ , $lD$ . Тогда $′ 1 ′ BB = 2AS,DD =2AS$ , откуда $′ 5 CC = 2AS$ . Пусть $G−$ точка пересечения плоскости $AEF$ с $CS$ . Тогда $SG :GC = 2:5$ . Далее,

2 1 2 1 2 VAEGFS = VAEFS +VEGFS = 3 ⋅3 ⋅VABDS + 3 ⋅ 3 ⋅7 ⋅VBCDS =

= 23 ⋅ 13 + 23 ⋅ 13 ⋅ 27 ⋅ 12VABCDS = 17VABCDS.

Стало быть, искомое отношение равно $1:6.$

Ответ:

$1 :6$

Ошибка.
Попробуйте повторить позже

Задача 10#63813

Дана треугольная призма $ABCA ′B ′C′$ с основанием $ABC$ и боковыми рёбрами $AA′,BB′,CC ′$ . На диагоналях $AB′,BC′,CA ′$ отмечены точки $D,E,F$ соответственно. Найдите отношение, в котором плоскость $DEF$ делит отрезок $′ AA$ , если $′ ′ AD :DB =1 :1,BE :EC = 1:2$ , $′ CF :FA =1 :3.$

Показать ответ и решение

Точки $D$ и $F$ лежат в плоскости $BCA ′$ . Обозначим через $G$ точку пересечения прямой $DF$ с прямой $BC$ . Из того, что $′ ′ AD :DB = 1:1,CF :FA =1:3$ , следует, что $1 GC = 2BC$ . Обозначим через $H$ точку пересечения прямой $GE$ с прямой $′ CC$ . Из того, что $1 GC = 2BC$ и $′ BE :EC = 1:2$ , следует, что $1 ′ CH =7CC$ . Обозначая через $K$ точку пересечения прямой $HF$ с прямой $′ AA$ , получаем $′ 3 ′ KA = 7AA$ . Стало быть, $′ A K :KA =3 :4.$

Ответ:

$3 :4$

Ошибка.
Попробуйте повторить позже

Задача 11#63892

Из вершины $D$ на плоскость основания $ABC$ пирамиды $ABCD$ опущена высота $DH$ . Найдите объем этой пирамиды, если известно, что площади треугольников $△HBC, △HAC, △HAB$ равны соответственно $2 1 4 9,3,9$ , и что все три плоских угла при вершине $D$ прямые.

Показать ответ и решение

Обозначим через $α,β,γ$ двугранные углы при ребрах $BC,AC,AB$ соответственно. Поскольку $DH ⊥ ABC,△HBC$ является ортогональной проекцией $△DBC$ . Следовательно, $S(△HBC )∕S(△DBC )= cosα$ . С другой стороны, $AD ⊥DBC$ , то есть $△DBC$ является ортогональной проекцией $△ABC$ , откуда

S(△DBC )∕S(△ABC )= cosα.

Учитывая, что $S(△ABC )= S(△ABH )+S (△BCH )+S(△ACH )= 1$ , получаем

S(△HBC-) ∘ -------- cosα =S(△DBC )= S(△DBC ) = S(△HBC ).

Аналогично,

∘-------- cosβ = S(△DAC )= ∘S(△HAC-) cosγ = S(△DAB )= S(△HAB )

Далее, поскольку плоские углы при вершине $D$ прямые,

√-∘ ------------------- V (A√BC∘D-)=-16AD-⋅BD-⋅CD-=-32--BD⋅2CD⋅ A√D∘⋅C2D-⋅ AD⋅2BD-=------------- = -23∘ S(△DBC )⋅S(△DAC )⋅S(△DAB )= 324S (△HBC )⋅S(△HAC )⋅S(△HAB )= = √23 429 ⋅ 13 ⋅ 49 = 24√4√9 3

Ответ:

$2√√42 9 43$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#70627

В основании прямой призмы $ABCA ′B′C ′$ лежит прямоугольный треугольник $ABC$ , такой что $AC = BC = 1$ . На ребре $A′B′$ верхнего основания (параллельном $AB$ ) отмечена точка $D$ , так что $′ ′ AD :DB =1 :2$ . Найдите радиус сферы, вписанной в тетраэдр $′ ABC D$ , если высота призмы равна $1.$

Источники: ДВИ - 2013, номер 7

Подсказки к задаче

Подсказка 1

Нам надо как-то найти радиус вписанной сферы. Его можно найти в формуле для объема тетраэдра. Можно ли как-то просто найти этот объем?

Подсказка 2

На самом деле он равен объему тетраэдра ABCD, ведь CC' параллельна основанию ABD. А объем тетраэдра легко найти: мы знаем, что площадь основания ABC- это 1/2, а высота- 1 ⇒объем равен 1/6. Что нам еще надо найти?

Подсказка 3

Как мы знаем, V=r*S/3, где V- объем тетраэдра, r- радиус сферы и S- площадь полной боковой поверхности. Тогда r=1/(2S). Легко заметить, что все стороны тетраэдра ABC'D легко находятся с помощью теоремы Пифагора. Тогда, зная все стороны, можно будет найти площади боковых граней и завершить решение. Я в вас верю!

Показать ответ и решение

$PIC$

Из теоремы Пифагора в треугольнике $ABC$ сторона $√- AB = 2.$ Так как $A ′D :DB′ = 1:2$ и $√- A′B′ = 2,$ то $√- √- A′D = 32,DB ′ = 232.$

Обозначим объём тетраэдра $ABC ′D$ , площадь его поверхности и радиус вписанной в него сферы, соответственно, как $V,S,r$ . Тогда $V = 13rS$ . Объём тетраэдра $ABC′D$ paвен объёму тетраэдра $ABCD$ , поскольку $CC′∥AA′$ . Стало быть,

V = 1∕6 =⇒ r= (2S)−1

Найдём все рёбра пирамиды $DABC ′.$ По теореме Пифагора в $△AA ′D:$

( √-)2 √ -- AD2 = A′A2+ A′D2 = 12+ -2- = 11 =⇒ AD = --11 3 9 3

Аналогично из теорем Пифагора в треугольниках $BB ′D,ACC′$ и $BCC ′ :$

┌│----(----)- -- │∘ 2 2√-2 2 √17 ′ ∘-2---2 √- ′ ∘ -2--2- √- BD = 1 + 3 = 3 ; AC = 1 + 1 = 2; BC = 1 +1 = 2

Так как $A′C′ = B′C′,$ то $∠C′A ′D = 45∘,$ тогда по теореме косинусов в $△DA ′C′ :$

′ 2 2 √2 1 5 ′ √5- C D = 9 + 1− 2⋅ 3-⋅√2-= 9 =⇒ C D= -3-

Теперь найдём площади всех граней пирамиды $DABC ′.$

$√- SADB =-22 .$ Так как $△AC ′B$ — равносторонний, то $√- SAC′B = -32 .$

Рассмотрим $△AC ′D.$ Пусть $∠AC′D =α,$ тогда по теореме косинусов

√ - ∘ -- 11= 2+ 5− 2⋅√2⋅--5⋅cosα =⇒ cosα= √2- =⇒ sinα = 3 9 9 3 10 5

1 √- √5 1 SAC′D = 2 ⋅ 2⋅-3-⋅sinα =√6

Рассмотрим $△BC ′D.$ Пусть $∠BC ′D = β,$ тогда по теореме косинусов

√ - 17-= 2+ 5− 2⋅√2⋅--5⋅cosβ =⇒ cosβ = √1- =⇒ sinβ = √3- 9 9 3 10 10

1 √ - √5 1 SBC′D = 2 ⋅ 2⋅-3-⋅sinβ = 2

Тогда площадь поверхности тетраэдра $′ ABC D$

( - - ∘-) S =SADB + SAC′B + SAC′D + SBC′D = 1 1+√ 2+√ 3+ 2 2 3

Остаётся воспользоваться соотношением $r =(2S)−1.$

Ответ:

$(1+ √2+ √3+ ∘ 2)−1 3$

Ошибка.
Попробуйте повторить позже

Задача 13#70626

Основанием пирамиды $SABCD$ является трапеция $ABCD$ с основаниями $BC$ и $AD$ такими, что $BC :AD = 2:5$ . Диагонали трапеции пересекаются в точке $E$ , а центр $O$ вписанной в пирамиду сферы лежит на отрезке $SE$ и делит его в отношении $SO :OE =7 :2$ . Найти площадь полной поверхности пирамиды, если площадь боковой грани $SBC$ равна $8.$

Источники: Вступительные на МехМат - 1999, задача 6

Подсказки к задаче

Подсказка 1

У нас уже есть площадь одной боковой грани. Может, тогда попытаемся найти площади остальных? Подумайте, как соотносятся между собой площади треугольников △SBC и △SAB...

Подсказка 2

Вроде как, напрямую связь между ними установить не получается. Давайте попробуем посмотреть на объемы тетраэдров SAOB и SBOC: они относятся как площади треугольников △SAB и △SBC. А как еще можно найти их отношение?

Подсказка 3

Т.к. объемы SABE и SBCE относятся как площади △ABE и △BEC (то есть как AE к EC), а также объемы OAEB и OBEC относятся как эти площади, то и их разности (то есть SAOB и SBOC) относятся как AE к EC. Тогда верно равенство S(△SAB)/S(△SBC)=AE/EC ⇒ S(△SAB)=20. Теперь найдите площади остальных боковых граней!

Подсказка 4

Нам осталось только найти площадь основания (назовем ее S₀). Мы знаем, что O делит SE в отношении 7/2. Тогда r=h*2/9, где r- радиус вписанной сферы, а h- высота пирамиды. Мы знаем, что V=S₀*h*1/3=S₀*r*3/2, где V- объем нашей пирамиды. Как еще, зная площади боковых граней, можно выразить V?

Подсказка 5

Через объемы тетраэдров ESAB, ESBC, ESCD и ESDA! Про них мы знаем, что высоты, опущенные из вершины E, равны r*9/7. Тогда мы без проблем сможем записать V через сумму объемов этих тетраэдров, приравнять к S₀*r*3/2 и найти площадь основания!

Показать ответ и решение

$PIC$