Ошибка.
Попробуйте повторить позже
Точка — центр вписанной в треугольник
окружности. Продолжение отрезка
за точку
пересекает описанную вокруг
треугольника
окружность в точке
Найдите угол
если
Источники:
Подсказка 1
Нам дали прямую, проходящую через центр вписанной окружности, которая пересекает описанную окружность треугольника. Какую тогда теорему можно вспомнить, связанную с такой конструкцией?
Подсказка 2
Верно, здесь можно применить лемму о трезубце. Откуда поймём, что OD = AD =CD. Теперь взглянем внимательно на условие. Нам дали отрезок AC=4OD, и выходит, мы знаем все стороны в равнобедренном треугольнике ACD. Вспомним ещё, что сумма противоположных углов в четырёхугольнике равна 180. Как отсюда можно попробовать найти угол B? Какую тогда теорему можно применить к равнобедренному треугольнику ADC?
Подсказка 3
Ага, давайте посчитаем ∠ADC по теореме косинусов. Но мы знаем, что ∠ABC = 180− ∠ADC. Осталось вспомнить, чему равен косинус смежного угла, и победа!
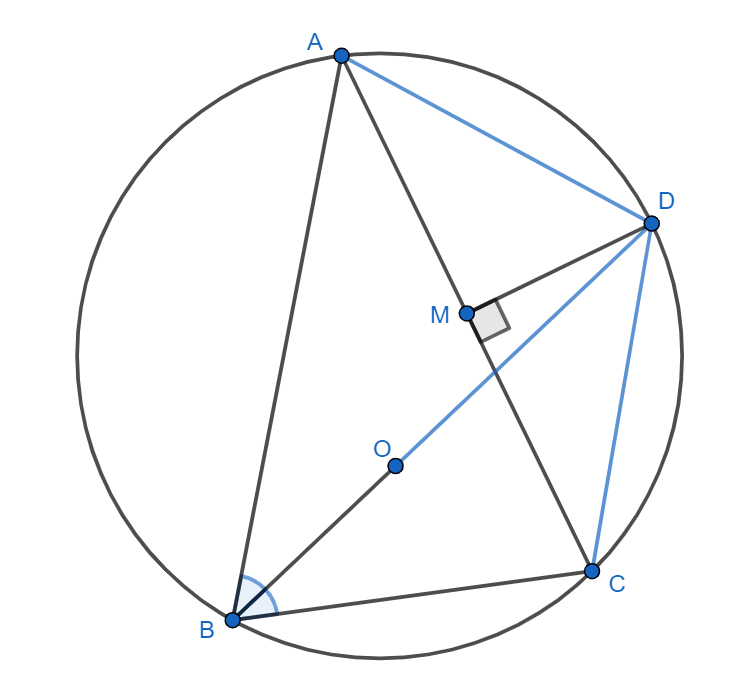
По лемме о трезубце
Первое решение.
Если то
Отсюда по теореме косинусов
Так как — вписанный четырехугольник, то
и
Значит,
Второе решение.
Пусть — середина
, тогда
, потому что треугольник
равнобедренный. Из условия
получаем,
что
. Следовательно,
. Далее нетрудно посчитать:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное обучение
в Школково
Для детей ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Брянской областей, а также школьникам, находящимся в пунктах временного размещения Крыма обучение на платформе бесплатное.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ или олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




