Стереометрия на ОММО —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Стереометрия на ОММО

Тема ОММО (Объединённая Межвузовская Математическая Олимпиада)

Стереометрия на ОММО

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела оммо (объединённая межвузовская математическая олимпиада)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#79606

Ортогональной проекцией правильной треугольной пирамиды на некоторую плоскость является параллелограмм с острым углом $60∘$ . Найдите объём пирамиды, если площадь её боковой поверхности равна 54.

Источники: ОММО - 2024, задача 8 (см. olympiads.mccme.ru)

Показать ответ и решение

Пусть сторона основания пирамиды $DABC$ с вершиной $D$ равна $a$ , а боковое ребро равно $b$ . Для построения проекции достаточно рассмотреть две пары скрещивающихся ребер, например $AB, CD,BC$ и $AD$ , проекции которых являются сторонами параллелограмма $A1B1C1D1.$

$PIC$

Пусть $MN$ — общий перпендикуляр пары рёбер $BC$ и $AD$ , а $PQ$ — общий перпендикуляр скрещивающихся рёбер $BC$ и $AD$ . Плоскость проекции $Ω$ параллельна как $MN$ , так и $P Q$ , поскольку ортогональной проекцией пирамиды является параллелограмм. Отрезки $MN$ и $PQ$ проектируются на плоскость $Ω$ без изменения длины в высоты параллелограмма $M1N1$ и $P1Q1$ , так как $ABB1A1$ и $DCC1D1$ обе перпендикулярны $Ω$ и будут параллельны друг другу, т.к. $A1B1C1D1$ — параллелограмм. То есть $MN$ не просто общий перпендикуляр $AB$ и $CD$ , но и общий перпендикуляр двух вышеописанных плоскостей. А значит ещё это и общий перпендикуляр для $A1B1$ и $C1D1.$

Поскольку пирамида правильная, $MN = PQ$ . Следовательно, $M1N1 = P1Q1.$

$PIC$

В параллелограмме $A1B1C1D1$ высоты, проведённые к смежным сторонам, равны — значит, параллелограмм является ромбом.

Пусть ребро $AB$ наклонено к плоскости $Ω$ под углом $α$ , тогда ребро $CD$ , которое перпендикулярно $AB$ , наклонено под углом $90∘− α$ . Отсюда $acosα= bsinα.$

Обозначим $ab = λ$ . Тогда $tgα= λ,A1B1 = acosα = √1a+λ2$ .

Найдём расстояние между скрещивающимися рёбрами правильной треугольной пирамиды как высоту сечения $DMC$ :

∘ ------ a√3- 2 a2 MC ⋅H = b⋅MN, 2 ⋅ b − 3 = b⋅MN

откуда

∘------ ∘----- MN = a2b 3b2− a2 = a2 3− λ2

Тогда синус острого угла пирамиды равен $sinφ = MA11ND11 = AM1NB1$ . Подставляя найденные выражения и данное в условии значение $φ =60∘$ , получим $- √32 = 12√3-−-λ2√1-+λ2-$ , откуда $λ= 0$ (что невозможно) или $λ2 =2.$

Площадь боковой поверхности пирамиды равна

∘ ----2- 2 √----2 S = 3a b2− a-= 3a-⋅-4−-λ- 2 4 4 λ

Подставив $S = 54$ и $λ= √2$ , найдём

a2 =72,b2 = a2= 36 λ2

Объём правильной пирамиды равен

a2∘ --2--2 √------- V = 12 3b − a = 6 108− 72=36

Ответ: 36

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#64569

В конус вписан цилиндр объема 9. Плоскость верхнего основания этого цилиндра отсекает от исходного конуса усеченный конус объемом 63. Найдите объем исходного конуса.

Источники: ОММО-2015, номер 10, (см.olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Запишем известные нам объёмы! В работе с усечённым конусом нам поможет формула, выражающая его объём через высоту и радиусы оснований. А чего нам не хватает для объёма искомого конуса?

Подсказка 2

Нам не хватает его высоты — она пока не фигурирует ни в одной из известных фигур. Зато у нас в обоих данных объёмах задействована высота усечённого конуса, которая дальше нам не очень нужна. Так выразим её из объёма цилиндра и подставим в объём усечённого конуса! Поработав с квадратным уравнением, мы отыщем отношение радиусов верхнего и нижнего оснований.

Подсказка 3

Отыскать высоту исходного конуса нам помогут подобные треугольники: рассмотрите осевое сечение этого конуса. Отношение радиусов поможет нам связать высоты исходного и усечённого конусов. Осталось немного повозиться с формулами, подставляя известные отношения, и задача убита!

Показать ответ и решение

$PIC$

Пусть высота и радиус исходного конуса равны $H$ и $R$ , а высота и радиус цилиндра равны $h$ и $r$ . Воспользуемся формулой для объема усеченного конуса: $( ) 13π R2+ Rr+ r2 h= 63$ . Также мы знаем, что $πr2h= 9$ . Поделив соответствующие части равенств получаем

( ) ( ) R- 2+ R- + 1= 63⋅3= 21 r r 9

Решая квадратное уравнение, получаем корни $4$ и $− 5,$ геометрический смысл имеет только положительный. $R∕r= 4,H-−h= 4, h-= 3 H H 4$ , откуда получаем для исходного конуса:

1 1 ( )(R )2 H 1 4 V = 3πR2H = 3 πr2h r- h-= 3 ⋅9 ⋅42⋅3 = 64

Ответ: 64

Ошибка.
Попробуйте повторить позже

Задача 3#64568

В прямоугольном параллелепипеде $ABCDA B C D 1 1 1 1$ с рёбрами $AB =3,AD = 4$ и $AA = 5 1$ проведены два сечения – плоскостью, проходящей через диагональ $A1C$ , и плоскостью, проходящей через диагональ $B1D$ . Найдите наибольшее возможное значение суммы площадей поверхностей многогранников, на которые эти сечения разбивают данный параллелепипед.

Источники: ОММО-2014, номер 10, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Нарисуйте картинку и попробуйте понять: что точно, вне зависимости от положения сечений будет содержаться в искомой сумме? Можем ли мы как-то избежать попадания в эту сумму какой-то части исходного параллелепипеда? А сколько раз туда попадут части наших сечений?

Подсказка 2

Итак, получается, что как бы ни были расположены сечения, их площади дважды войдут в искомые площади поверхностей. Значит надо эти площади максимизировать!

Подсказка 3

Какой фигурой будет являться каждое сечение? Как площади сечений связаны с длинами диагоналей? Исследуйте, где должны быть расположены вершины параллелограмма-сечения, чтобы расстояние до диагонали параллелепипеда было наибольшим.

Подсказка 4

Осталось лишь посчитать все нужные длины, призвав на помощь теорему Пифагора. Будьте внимательны к арифметике и задача окажется убита!

Показать ответ и решение

Сумма площадей поверхностей многогранников, на которые разбивается параллелепипед сечениями, равна сумме площади поверхности параллелепипеда и площадей внутренних поверхностей. Сумма площадей внутренних поверхностей равна удвоенной сумме площадей сечений.

Найдем наибольшую возможную площадь сечения, проходящего через диагональ $XY$ произвольного параллелепипеда с ребрами $a≤ b≤ c$ . Сечением является параллелограмм $ZXT Y$ , вершины которого лежат на противоположных рёбрах параллелепипеда. Площадь параллелограмма равна произведению длины диагонали $XY$ на расстояние от точки $Z$ до $XY$ .

$PIC$

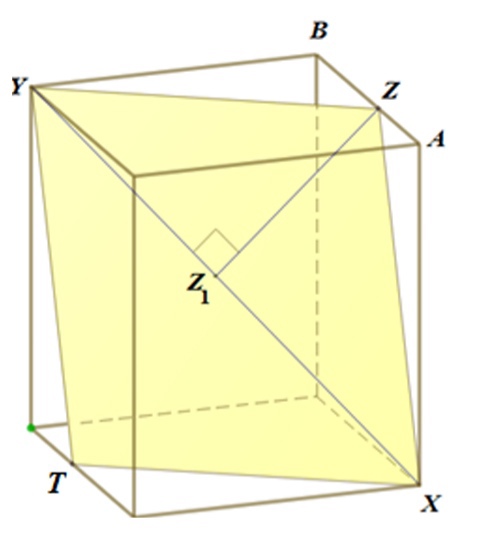
Рассмотрим проекцию параллелепипеда на плоскость, перпендикулярную диагонали $XY$ . На рисунке видно, что расстояние от точки $Z$ ломаной $ABC$ до точки $Y$ , то есть до диагонали $XY$ , наибольшее, если $Z$ совпадает с одной из вершин $A,B$ или $C$ .

$PIC$

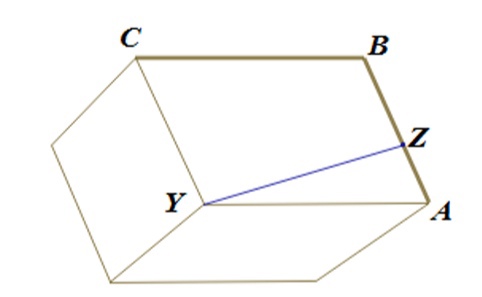
Значит, сечение проходит через одно из ребер параллелепипеда. Таким образом, наибольшую площадь имеет одно из диагональных сечений. Все эти сечения являются прямоугольниками. Найдем наибольшую из их площадей

∘----- ∘------ ∘ ------ S1 = a b2+ c2,S2 = b a2+ c2 и S3 =c b2+ a2.

Из условия $a ≤b ≤c$ следует, что, $22 22 2 2 2 2 a b +a c ≤c b +a c$ , и $22 22 22 22 a b+ c b ≤c b+ a c$ . Поэтому $S1 ≤ S3$ и $S2 ≤ S3$ . Значит, наибольшую площадь имеет сечение, проходящее через наибольшее ребро. По условию наибольшую длину имеет ребро $AA1$ , значит, наибольшую площадь $√-2---2 5 4 + 3 = 25$ имеют сечения $AA1C1C$ и $BB1D1D$ .

$PIC$

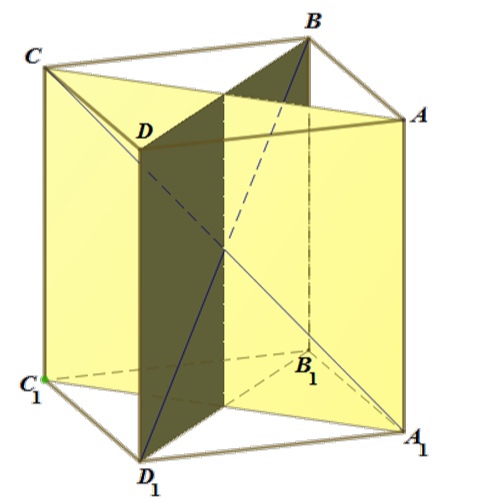
Сумма площадей поверхностей многогранников, на которые разбивается параллелепипед этими сечениями (см. рисунок), равна

2(AA1⋅AB + AA1⋅AD +AB ⋅AD )+4 ⋅25= 194.

Ответ: 194

Ошибка.
Попробуйте повторить позже

Задача 4#38690

Единичный куб $ABCDA B C D 1 1 1 1$ повёрнут на $90∘$ вокруг прямой, проходящей через середины противоположных рёбер $AD$ и $B C 1 1$ . Найдите объём общей части исходного куба и повёрнутого.

Источники: ОММО-2013, номер 10, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Итак, для начала надо внимательно разобраться с получающейся фигурой. Удобно начать построение с поворота рёбер AD и B₁C₁. Похожа ли общая часть кубов на какую-то известную нам фигуру? Если нет, то подумайте как можно её разбить на составляющие.

Подсказка 2

Работать с такого типа фигурой можно через сумму объёмов составляющих её частей. Или же через разность: вычитая удобные части из фигуры, содержащей искомую. Рассмотрим способ через сумму — наш многогранник удачно разбивается на параллелепипед и две правильные четырёхугольные пирамиды.

Подсказка 3

Найти все нужные длины нам поможет Пифагор: рассмотрите одну из граней исходного куба и возвышающуюся над ней часть нового куба. Аккуратный счёт поможет вам узнать, где пересекутся рёбра нового и исходного кубов.

Подсказка 4

Также, с помощью Пифагора мы сможем отыскать и все рёбра искомого многогранника. Осталось лишь отыскать объёмы всех составных частей и сложить их. Задача убита!

Показать ответ и решение

$PIC$

Пусть $S$ и $S1$ — середины $AD$ и $B1C1$ , а куб после поворота переходит в $A′B′C ′D′A′1B′1C′1D′1$ . Общая часть будет объединением прямоугольного параллелепипеда $EFGHE1F1G1H1$ и двух симметричных правильных четырёхугольных пирамид $SEFGH$ и $S1E1F1G1H1$ , найдём их объёмы.

$PIC$

Сторона основания пирамиды равна стороне квадрата, то есть единице. Далее оба квадрата симметричны относительно $AB1C1D$ , потому $E1√F1 √1- E1B1 = F1B1 = 2 = 2$ . Из $△E1B1S1$ имеем $∘-1--1 √3 E1S1 = 2 + 4 = 2$ — боковая сторона пирамиды. Отсюда легко найти её высоту, которая равна $1 2$ , тогда объём пирамиды равен $1 1 1 3 ⋅1 ⋅2 = 6$ .

$PIC$

Поскольку $A1E1 = A1E = 1− 1√2$ ( $EE1 ⊥E1F1$ , которая по доказанному образует углы $45∘$ со сторонами), то $EE1 = √2 − 1$ , $EF = EH = 1$ , как стороны квадрата, отсюда объём параллелепипеда $√2 − 1$ .