ТурЛом (турнир Ломоносова) —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
ТурЛом (турнир Ломоносова)

Тема ТурЛом (турнир Ломоносова)

ТурЛом (турнир Ломоносова)

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Разделы подтемы ТурЛом (турнир Ломоносова)

Отбор Турлома

Последовательности и прогрессии на Турломе

Квадратные трёхчлены на Турломе

Многочлены на Турломе

Тождественные преобразования на Турломе

Системы на Турломе

Планиметрия на Турломе

Теория чисел на Турломе

Комбинаторика на Турломе: графы, игры, клетчатые задачи, Дирихле

Комбигео на Турломе

Неравенства на Турломе

Подтемы раздела турлом (турнир ломоносова)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#68035

Авантюрист прибыл на остров, где живёт племя аборигенов, и пытается понять их язык. На данный момент ему известно следующее: 1. в языке всего две буквы $A$ и $B,$ каждая последовательность букв образует слово, у которого есть некоторое значение; 2. несмотря на то, что слов бесконечно много, значений у слов конечное количество;

Авантюрист придумал обозначение для слов, имеющих одинаковое значение: он стал писать между ними знак равенства «=». 3. если $w1 =w2,$ то для любых слов $s$ и $t$ выполнены равенства $sw1t=$ $sw2t,sw1 =sw2,w1t= w2t$ (для слов $x$ и $y$ под $xy$ понимается слово, полученное приписыванием к слову $x$ справа слова $y);$ другими словами, если в некотором слове заменить его подслово на слово с тем же значением, то значение слова от этого не изменится. Докажите, что если $ABB = B,$ то $BAB =B.$

Источники: Турнир Ломоносова-2023, 11.5 (см. turlom.olimpiada.ru)

Подсказки к задаче

Подсказка 1

Понятно, что хочется цепочкой слов что-то делать с ВАВ, причем используя АВВ. Не хватает В в конце ВАВ…подумаем в сторону В, сколько можно их добавить?

Подсказка 2

Если мы сколько-то добавим, заменим АВВ на В, то избавимся от А! Тогда у нас останется множество В-шэк, от которого хотим прийти к одной В… Тогда подумаем, а сколько В-шэк на какое количество В-шэк можно заменить?

Подсказка 3

Какое-то количество В-шэк точно можно заменять на меньшее количество (в силу конечного количества значений). Попробуем с помощью цепочки равенств доказать, что какое-то количество В можно заменять на одну В! Останься лишь воспользоваться подсказкой 2)

Показать доказательство

Поскольку различных значений у слов конечное количество, то среди слов $B,BB,...$ найдутся два с одинаковым значением. Пусть это слова из $n$ и $m$ $(n< m)$ букв $B :$

B◟B◝..◜.B◞= B◟B-.◝◜..B◞. n m

Докажем, что слово $B$ имеет то же значение, что и слово из $k= m − n +1 ≥2$ букв $B.$ Если для такой пары оказывается, что $n = 1,$ то это верно. В противном случае при $n ≥2 :$

BB ...B =B BB ...B =ABB BB...B= ABB ...B= ABB ...B = ABB BB ...B = ◟-◝n◜−1-◞ ◟-◝n◜−2-◞ ◟n◝−◜2-◞ ◟--◝n◜-◞ ◟--◝m◜-◞ ◟-◝m◜−2-◞

= BB◟B-.◝.◜.B◞= B◟B◝..◜.B◞. m−2 m −1

То есть одинаковые значения имеют слова из $n− 1,m − 1$ букв. Отсюда и следует верность утверждения, если продолжать до тех пор, пока $n ⁄=1.$

Тогда:

BAB = BA B◟B◝..◜.B◞=BABB B◟B◝..◜.B◞ =BB B◟B-.◝◜..B◞= B◟B.◝.◜.B◞= B. k k− 2 k−2 k

Что и требовалось доказать.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#68034

Положительные числа $a,a ,...,a 1 2 n$ таковы, что $a + a +...+a > 2023. 1 2 n$ Докажите, что

√-- 3√-- n√-- a1⋅a1 +a2⋅ a2+ a3⋅ a3+ ...+ an an >1000.

Источники: Турнир Ломоносова-2023, 11.4 (см.turlom.olimpiada.ru)

Подсказки к задаче

Подсказка 1

Нужно как-то прийти к корням, причем необычной степени…нам известна сумма всех чисел, а также сумма всех чисел, но с какими-то множителями… Попробуем выцепить из всех чисел группу каких-то больших, у которых указанная в условии сумма с корнями будет точно больше 1000.

Подсказка 2

Попробуем отделить от всех чисел такие, что a_m > 1/2^m. Что можно сказать про сумму этих чисел и про сумму этих чисел, но в произведении с корнями?(какие даны в условии)

Подсказка 3

Их сумма хотя бы 2022, а корни можно связать с 1/2)

Показать доказательство

Разобьем все эти числа на две группы. Число $a k$ попадает в первую группу, если $a < -1. k 2k$ А иначе попадает во вторую группу. Тогда сумма чисел в первой группе меньше, чем

1 1 1 1 2 + 4 +⋅⋅⋅+2n = 1− 2n-< 1.

Тогда сумма чисел во второй группе будет хотя бы $2023− 1= 2022.$ Пусть $am$ находится во второй группе, тогда, так как все числа положительны:

√ --- 1 m am ≥ 2

Значит,

am ⋅ m√am-≥ am. 2

Тогда все слагаемые из второй группы дают вклад в

a1⋅a1 +a2⋅√a2+ a3⋅ 3√a3+ ...+ an n√an >1000.

Который составляет хотя бы половину от суммы всех чисел этой группы, то есть точно больше $20222= 1011.$ Следовательно, верно и требуемое.

Ошибка.
Попробуйте повторить позже

Задача 3#68033

Внутри окружности $ω$ проведены две перпендикулярные хорды, пересекающиеся в точке $P;$ точки $M 1$ и $M 2$ их середины. Прямая $M1M2$ пересекает $ω$ в точках $A$ и $B,$ причём $M1$ лежит между $A$ и $M2.$ Какие значения может принимать разность $BM2 − AM1,$ если $PM1 = 15,PM2 = 20?$

Источники: Турнир Ломоносова-2023, 11.3 (см. turlom.olimpiada.ru)

Подсказки к задаче

Подсказка 1

Такс, у нас есть две хорды и их середины, есть еще и третья хорда, у которой мы тоже можем отметить середину! Какое доп.построение хочется сделать?

Подсказка 2

Да, мы знаем, что отрезок проведённый из центра окружности к середине хорды — перпендикулярен хорде, поэтому давайте проведём три таких отрезочка!(к каждой из хорд). Что можно сказать про полученный четырёхугольник OM₁PM₂, где O - центр окружности?

Подсказка 3

Верно, это прямоугольник! Тогда мы можем найти M₁M₂ из прямоугольного треугольника! Осталось понять, как от M₁M₂ прийти к исходной разности в вопросе задачи, учитывая, что M - середина AB!

Показать ответ и решение

$PIC$

Пусть $O −$ центр окружности, $M$ — середина отрезка $AB.$ Поскольку отрезок, соединяющий центр окружности с серединой хорды перпендикулярен этой хорде,

∠OM1P =∠OM2P =∠OMA = 90∘.

Заметим, что

BM2 − AM1 = (BM − MM2 )− (AM − MM1 ) =MM1 − MM2,

т.к. $AM = BM.$

Далее, в четырёхугольнике $OM1P M2$ три угла прямые, т.е. этот четырёхугольник — прямоугольник,

OM1 =P M2 = 20,OM2 = PM1 = 15,∠M1OM2 = 90∘.

Тогда в прямоугольном треугольнике $OM1M2$ проведена высота $OM$ на гипотенузу. По теореме Пифагора $∘ ---2----2- √ ------- M1M2 = OM 1 +OM 2 = 400 +225= 25.$ Так как катет есть среднее геометрическое гипотенузы и своей проекции на неё, то $MM1 =16,MM2 = 9.$ Откуда получаем ответ.

Ответ: 7

Ошибка.
Попробуйте повторить позже

Задача 4#68032

Арифметическая прогрессия $a ,a,... 1 2$ задана первыми двумя членами: $a = 381,a = 406. 1 2$ Определим последовательность $b k$ следующим образом: $b1 = a1 = 381,bk+1 =bk⋅ak+1$ для каждого $k ≥1.$ Тогда $b2 = 381⋅406= 154686.$ В записи этого числа используется 5 различных цифр: $1,4,5,6$ и 8. А какое наименьшее количество различных цифр может использоваться в записи числа $bk$ для натурального $k?$

Источники: Турнир Ломоносова-2023, 11.2 (см. turlom.olimpiada.ru)

Подсказки к задаче

Подсказка 1

Нам дали всего лишь два члена каждой последовательности… Кажется, это маловато, поэтому давайте посчитаем еще несколько членов каждой из последовательностей! Что интересное мы видим?

Подсказка 2

Да, третий член последовательности b имеет всего лишь 2 различные цифры в своей записи! Что осталось сделать, чтобы сказать, что 2 — это ответ на вопрос задачи?

Подсказка 3

Да, достаточно показать, что любой член последовательности b не может состоять из одной цифры! Перебирать дальше члены последовательностей не имеет смысла, ведь числа получаются огромные, что может нам помочь в таком случае?

Подсказка 4

Конечно, надо подумать про делимость всех членов b, после третьего! Поскольку a₄ кратно 4, то все члены последовательности b, начиная с 4-ого кратны четырём! А что еще можно сказать про каждый член последовательности b?

Подсказка 5

Верно, каждый из них оканчивается на 6! Что осталось показать, чтобы решить задачу?

Показать ответ и решение

Оценка. Докажем, что всего одна цифра в записи $b k$ не может быть. Найдем $b ,a : 3 4$

a3 = a2+(a2− a1)= 431;

a4 = a3+(a3− a2)= 456;

b = b ⋅a = 66 669 666. 3 2 3

Заметим, что $a4$ делится на $4,$ значит $b4$ и все $bk$ будут делится на $4.$ Кроме того, каждое из $ak$ оканчивается или на $1,$ или на $6.$ Поэтому все $bk$ при $k ≥4$ будут оканчиваться на $6(6⋅1= 6,6⋅6 =36).$ Получается, если в записи $bk,k≥ 4,$ будет всего одна цифра, то это цифра $6.$ Тогда последние две цифры $bk$ это $66,$ т.е. $bk$ не делится на $4,$ противоречие.

Пример. В записи $b3$ используются только две цифры.

Ответ: 2

Ошибка.
Попробуйте повторить позже

Задача 5#68031

Действительные числа $x$ и $y$ таковы, что

5 3 x +y = y+ x = 23

Какое наибольшее значение может принимать произведение $xy?$

Источники: Турнир Ломоносова-2023, 11.1 (см. turlom.olimpiada.ru)

Подсказки к задаче

Подсказка 1

Давайте запишем наше условие как системку, что два левых выражения равны 23. Понятно, что x, y не нули. Поэтому что можно сделать в системе, чтобы получить где-то xy?

Подсказка 2

Домножить одно из уравнений на x, а другое на y! И выйдет что-то вида xy+3 = 23x, xy+5 = 23y. А что стоит сделать теперь, чтобы вообще все было только через xy?

Подсказка 3

Перемножить два этих уравнения) Дальше делаем замену и решаем задачу окончательно!

Показать ответ и решение

При условии того, что обе переменные не равны нулю, имеем:

{ xy+ 5= 23y xy+ 3= 23x.

Значит:

(xy+ 5)(xy+ 3) =232xy

Пусть $t=xy :$

t2+ 8t+15 =529t

t2− 521t+15= 0

Тогда получим:

√ ------ t= 521±--271-381. 2

Докажем, что наибольший корень реализуется. Действительно, из обоих уравнений получаем $x,y,$ подставляя $xy.$ Они подходят, так как наши преобразования были равносильны с учетом того, что $x⁄= 0,y ⁄=0.$

Ответ:

$521+√271381 2$

Ошибка.
Попробуйте повторить позже

Задача 6#76580

Пусть $k$ — целое неотрицательное число, не превосходящее $1001.$ На доске написаны $k$ единиц и $1001− k$ нулей, т.е. всего на доске $1001$ число. Саша и Марина играют в игру, делая ходы по очереди, начинает Саша. В свой ход Саша может заменить два каких-то числа на их произведение. Марина в свой ход может заменить два одинаковых числа на ноль, а два разных числа на $1.$ Так они ходят до тех пор, пока на доске не останется ровно одно число. Если это единица — выигрывает Саша, если ноль — Марина. При каких $k$ выигрывает Саша?

Источники: Турнир Ломоносова-2022, 11.5

Подсказки к задаче

Подсказка 1

В подобных задачах, когда возможных значений слишком много, бывает очень полезно начать с чего-то малого и простого. Подумайте, что будет, если в какой-то момент на доске останется только 1 единица. Кто в таком случае однозначно может победить? Не забудьте, что перед ходом Саши чисел нечётное количество, а перед ходом Марины - чётное

Подсказка 2

Конечно, неважно, чей сейчас ход: если на доске только одна единица, Саша однозначно победит. Теперь, продолжая разбирать простые случаи, попробуйте рассмотреть k = 1 или 2. Получится ли придумать победную стратегию для Саши?

Подсказка 3

Верно, при k=1 всё очевидно, а при k=2 первым ходом Саши ситуация сводится к одной единице. При этом если взять k ещё меньше, то получится, что на доске одни нули, и Марина сразу побеждает. А что происходит при бо́льших значениях k?

Подсказка 4

Если единиц три, то при любой стратегии Саши Марина может превратить все числа в нули. Обратите внимание, что при бо́льших k это также работает (ведь Саша может уменьшать количество единиц только на 1 за раз, и никто не может его увеличивать, так что общее количество единиц обязательно пройдёт через тройку). Теперь остаётся только аккуратно это доказать и грамотно расписать ситуацию для каждого значения k.

Показать ответ и решение

Заметим, для начала, что если на доске чётное количество чисел, то ходит Марина, а если нечётное — Саша.

Докажем, что если на доске ровно одна единица, то выигрывает Саша. Если сейчас ход Марины, то она не может убрать ровно одну единицу, поэтому после её хода тоже останется ровно одна единица. Если сейчас ход Саши, то или игра уже закончилась (и на доске всего одна единица), или помимо этой одной единицы есть ещё хотя бы два нуля, которые Саша и перемножает, передавая Марине ситуацию с одной единицей.

Тогда, если $k= 1,$ то Саша сразу находится в выигрышном для себя положении, а если $k= 2,$ то он должен первым ходом перемножить две единицы и передать Марине ситуацию ровно с одной единицей.

Докажем теперь, что если $k= 0$ или $k ≥3,$ то выигрывает Марина. Заметим, что если в какой-то момент на доске окажутся одни нули, то Марина выигрывает. Тогда при $k= 0$ Марина точно уже выиграет.

Назовём ситуацию, в которой на доске есть хотя бы три единицы и хотя бы один ноль — разнообразной. Докажем, что если на доске образовалась разнообразная ситуация, то выигрывает Марина.

Пусть сейчас ход Саши. Если он оставляет ситуацию разнообразной - хорошо. Если же он сделал ситуацию не разнообразной, то поскольку убрать ноль он не может, как и убрать сразу две единицы, то сейчас на доске ровно две единицы, а остальные нули. Марина своим следующим ходом заменяет эти две единицы на $0,$ и теперь на доске одни нули.

Пусть сейчас ход Марины. Перед ней точно есть $1,1,1,0.$ Если есть какие-то ещё числа, то их чётное количество, то есть хотя бы два, поэтому она может сделать ход с ними, оставив ситуацию разнообразной. Если же других чисел нет, то Марина меняет $1,0$ на $1,$ оставляя Саше $1,1,1;$ тогда он делает ход и оставляет $1,1,$ и Марина выигрывает, делая после этого $0.$

Осталось заметить, что при $k≥ 3$ и $k⁄= 1001,$ ситуация на доске уже разнообразная, а при $k= 1001,$ Марина может сделать её разнообразной своим первым ходом.

Ответ:

$1,2$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#76579

При каком наименьшем $n$ все натуральные делители числа $n$ можно поделить на три группы, суммы в которых равны? Если группа состоит из одного числа, то сумма чисел в этой группе равна этому одному числу.

Источники: Турнир Ломоносова-2022, 11.4

Подсказки к задаче

Подсказка 1

Вспомните для начала, как считать сумму делителей числа, или выведите. Это несложно. Давайте подумаем в общем о природе групп. Какая может быть минимальная сумма делителей у одной группы?

Подсказка 2

Верно, так как в какую-то группу попадёт число n, а это делитель n, то сумма должна быть равна минимум n. Тогда о каком примере можно подумать? Попробуйте перебрать не слишком большие числа, где сумма делителей будет хотя бы 3n.

Подсказка 3

Да, это число 120, сумма его делителей 360. Поэтому у нас получатся группы (120), (40, 20, 60) и в последней группе остальные числа. Отсюда получается и идея для доказательства оценки. Если число будет меньше 120, то сумма его делителей будет меньше 3n. Как тогда можно оценить самым грубым образом сумму делителей в общем виде?

Подсказка 4

Верно, если предположить, что геометрическая прогрессия бесконечная, то это запишется просто как n на произведение дробей вида p/p-1. Как можно оценить сколько простых делителей входит в n при наших условиях?

Подсказка 5

Да, давайте просто переберём все наши возможности. Это когда n просто степень простого числа, когда n произведение двух степеней простых. Рассмотрев ещё, что будет происходить с 3 делителями или больше, получим, что n содержит ровно 3 простых делителя. А можем ли мы сказать, из каких точно делителей должно состоять n?

Подсказка 6

Верно, маленьким перебором получится, что n представляется в одном из трёх видов 2*3²*p, 2²*3*p, 2*3*p, где p простое число. Теперь только осталось разобрать их, и мы получим оценку на число 120. Победа!

Показать ответ и решение

Заметим, что $120 =23⋅3⋅5,$ поэтому сумма всех делителей числа $120$ равна $(1+2 +4+ 8)(1+ 3)(1+ 5) =15⋅4⋅6= 360.$ Поэтому нам надо поделить делители в группы с суммой $120.$ Подойдут группы ${120}$ , ${20,40,60}$ и все оставшиеся числа.

Докажем теперь, что делители чисел меньше $120$ нельзя поделить на три группы с равной суммой. Для этого докажем, что если $n$ меньше $120,$ то сумма делителей числа $n$ меньше $3n.$ Поскольку у $n$ всегда есть делитель, равный $n,$ то сумма в одной группе должна быть хотя бы $n,$ на этом и будет построено противоречие.

Вспомним, что сумма делителей числа $α1α2 αs n= p1 p2 ...ps$ равняется

( )( ) ( ) σ(n)= 1+ p1 +p21+ ...+ pα11 1+ p2+p22+ ...+ pα22 ...1+ ps+ p2s +...+ pαss

Следовательно

( 1 1 ) ( 1 1 ) ( 1 ) σ(n)= n 1 +p1 +...+ pα11 ... 1+ ps + ...+ pαss < n 1 +p1 +... ...

( ) ... 1+ 1-+ ... = n⋅--p1-...-ps-- ps p1− 1 ps− 1

В неравенстве мы заменили конечную сумму геометрической прогрессии на бесконечную.

Пусть теперь $n$ — некоторое число. Если у $n= pa,$ то

--p- σ(n)< n⋅p− 1 ≤2n< 3n,

поскольку число $p 1 p−-1 = 1+ p−1$ тем больше, чем меньше $p.$

Аналогично, если $n =pa⋅qb,$ то

p q 2 3 σ(n)< n⋅p−-1q−-1 ≤n2-− 1 ⋅3− 1-= 3n

Итак, если $σ(n)≥3n,$ то в разложение $n$ входит хотя бы 3 простых числа. Поскольку уже $2 ⋅3 ⋅5 ⋅7 =$ $210> 120,$ то нас интересуют лишь $n,$ в разложении которых ровно три простых числа.

Если среди этих простых чисел нет $2:$ если среди них нет и $3,$ то $n ≥$ $5 ⋅7 ⋅11 >120,$ значит $3$ есть; если нет $5,$ то $n ≥3⋅7⋅11> 120,$ значит и $5$ есть; если нет $7,$ то $n≥ 3⋅5⋅11 >120,$ значит и $7$ есть. Тогда $n =3⋅5⋅7= 105$ (добавление ещё одного простого сделает $n$ больше $120$ ), сумма делителей которого равна $(1 +3)(1+ 5)(1+ 7)=192< 315.$ Значит, $n$ обязательно делится на $2.$

Пусть третий простой делитель $p.$ Заметим, что $2⋅3⋅p≥ 30;$ поскольку мы ищем $n< 120,$ то домножить $2⋅3⋅p$ мы можем максимум на $3.$ Итак, получили всего немного вариантов: или $n =2 ⋅32⋅p$ , или $n =22⋅3⋅p$ , или $n =2 ⋅3 ⋅p.$

В первом случае при $p≥ 7$ получаем $n ≥ 126,$ при $p =5$ получаем $n =90,$ а

σ(90) =(1+ 2)(1+3 +9)(1 +5)= 234 <270

Во втором случае,

σ(n)= (1 +2+ 4)(1+ 3)(1+ p)=n ⋅ 7⋅ 4 ⋅ p+1 4 3 p

Если $σ(n)≥ 3n,$ то

p+-1≥ 9 p 7

Отсюда $p< 5,$ что неверно.

Аналогично, в третьем случае

σ(n) =(1+ 2)(1+ 3)(1+p)= n⋅ 3 ⋅ 4⋅ p+-1 2 3 p

Отсюда $p+1 p$ должно быть хотя бы $3 2,$ что неверно при $p≥ 5.$

Ответ: 120

Ошибка.
Попробуйте повторить позже

Задача 8#76578

Пусть $O$ — центр описанной окружности, $G$ — точка пересечения медиан остроугольного треугольника $ABC.$ Прямая, перпендикулярная $OG$ , проходящая через точку $G,$ пересекает отрезок $BC$ в точке $K.$ Касательная к описанной окружности треугольника $ABC$ в точке $A$ пересекает прямую $KG$ в точке $L.$ Найдите величину угла $∠ACB,$ если $∘ ∠LOK = 155 ,$ а $∘ ∠ABC =53 .$

Источники: Турнир Ломоносова-2022, 11.3

Подсказки к задаче

Подсказка 1

Нас просят найти какой-то угол и из условий нам дали значения каких-то углов. В таких задачах, где надо работать с углами, очень часто могут помочь вписанные четырёхугольники. Давайте попробуем найти такие, которые бы смогли перенести наши уголочки из условия в какие-то более удобные места.

Подсказка 2

Попробуйте посмотреть на GMKO и AOGL: они оба содержат части угла из условия LOK, а так же переносят их ближе к треугольнику AMC, а что мы можем сказать про угол ABC, можем ли мы его тоже перенести поближе к AMC?

Подсказка 3

Верно, ABC равен углу LAC, как угол между касательной и хордой, остаётся только внимательно присмотреться к треугольнику AMC и писать ответ.

Показать ответ и решение

Пусть $M$ — середина стороны $BC;$ поскольку $AM$ — медиана, то точки $G$ лежит на $AM.$

$PIC$

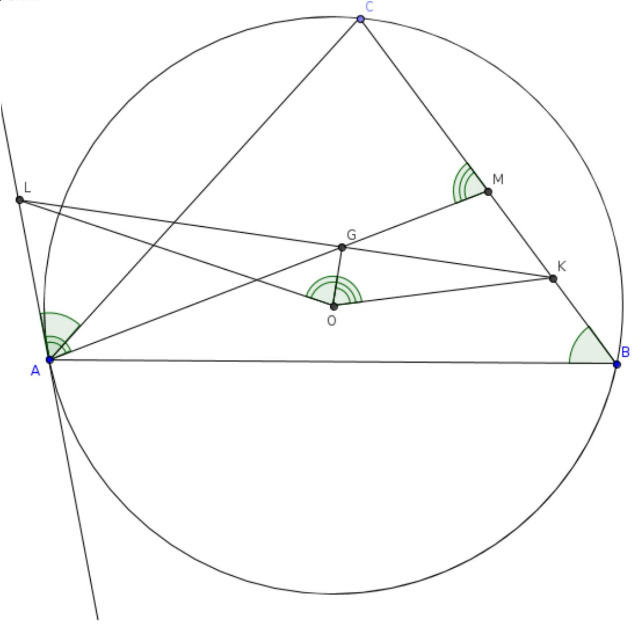
Четырёхугольник $OGMK$ — вписанный, так как $∠OGK =90∘ = ∠OMK$ (первое равенство по условию, второе следует из того, что $OM$ — серединный перпендикуляр к $BC$ ), откуда $∠GOK = 180∘ − ∠GMK =$ $∠GMC.$

Четырёхугольник $OGLA$ — вписанный, так как $∠OGL = 90∘ = ∠OAL$ (первое равенство по условию, второе следует из того, что $OA$ — радиус, а $AL$ — касательная к описанной окружности треугольника $ABC$ ), откуда $∠GOL =∠GAL.$

Значит,

∠ACB = 180∘− (∠CAM + ∠CMA )= 180∘ − (∠LAM + ∠CMA − ∠LAC )=

= 180∘− (∠LOG +∠GOK − ∠ABC )= 180∘ − (∠LOK − ∠ABC )=

= 180∘ − (155∘− 53∘) =78∘

Первое равенство следует из суммы углов треугольника $AMC.$

Ответ:

$78∘$

Ошибка.
Попробуйте повторить позже

Задача 9#76577

У Ярослава есть $N$ замков, пронумерованных числами от 1 до $N,$ расположенных по кругу в порядке увеличения номеров от 1 до $N$ по часовой стрелке. В начальный момент времени все замки открыты. Ярослав начинает с замка с номером 1 и движется всегда по часовой стрелке. Если Ярослав находится у замка с номером $k,$ то:

если открытых замков сейчас суммарно больше $k,$ то Ярослав закрывает следующие по часовой стрелке $k$ открытых замков, и переходит к следующему после этого открытому замку (возможно, снова к замку с номером $k$ );
если открытых замков сейчас суммарно не больше $k,$ то Ярослав закрывает все замки, кроме замка с номером $k,$ и заканчивает (таким образом, остаётся открытым только замок с номером $k$ ).

При каком наименьшем $N > 2022$ Ярослав оставит в конце открытым замок с номером 1?

Источники: Турнир Ломоносова-2022, 11.2

Подсказки к задаче

Подсказка 1

Попробуйте посмотреть, какие замки точно останутся закрытыми, а какие открытыми, когда Ярослав сделал какое-то кол-во шагов, но всё ещё на первом круге.

Подсказка 2

Мы понимаем, что 1,3,7,15,31,63,127,255,511,1023 будут открыты. Посмотрите, что происходит в моменте, когда Ярослав стоит на 1023 замке, возможно, мы сможем получить оценку на N? Обратите внимание на то, что после замка с номером k он либо остаётся на нём же, либо переходит в замок с номером 2k+1.

Подсказка 3

Да, если N < 2046, то он гарантированно закроет замок с номером 1, а что будет при N = 2046? В этой задаче хорошо, что пример придумывать не нужно, а можно просто проверить, выполняется ли условие после проделанного алгоритма или нет.

Показать ответ и решение

Легко видеть, что Ярослав будет находится вначале у замка $1,$ потом — $3,7,15,31,63,127,255,511,1023.$

Если $N <2046,$ то следующим действием Ярослав закроет замки с номерами $1024,1025,...,N,1$ и, возможно, ещё какие-то. В любом случае, замок под номером $1$ останется закрытым.

Если $N =2046,$ то дальше Ярослав закроет все замки с номерами от $1024$ до $2046$ и вновь встанет у замка с номером $1.$ Сейчас открыты замки $1,3,7,15,31,63,127,255,511,1023.$ Дальше Ярослав закрывает замок $3$ и переходит к замку $7,$ потом закрывает замки $15,31,...,1023,$ и переходит к замку $1,$ который и оставляет открытым.

Ответ: 2046

Ошибка.
Попробуйте повторить позже

Задача 10#76576

Действительные числа $x$ и $y$ таковы, что $x(x+ 1)y =6,$ а $x3(x3+ 1)y3 = 126.$ Какие значения может принимать выражение $2( 2 ) 2 x x + 1y ?$ Укажите все возможные ответы и докажите, что других нет.

Подсказки к задаче

Подсказка 1

У нас есть система уравнений, казалось бы. И мы хотели бы ее решить. Однако, решать в лоб - долго и можно ошибиться. Нам нужно как-то составить из этой системы уравнение на x. При этом, y в нашей системе в одной форме(то есть, на него просто умножают все выражение в конце, на какую то степень). Как тогда можно составить уравнение, в котором есть только х?

Подсказка 2

Верно, возведем первое в куб. Тогда, у нас получится (xy)^3 * (x + 1)^3 = 6^3, (xy)^3 * (x^3 + 1) = 126. Поделим первое на второе и получим уравнение на х (квадратное, ведь x + 1 сократился, когда поделили). Значит, нашли корни. Осталось найти y и подставить в искомое выражение.

Показать ответ и решение

Возведём первое равенство в куб и поделим на второе:

-63- x3(x+-1)3y3 126 = x3(x3+1)y3

Отсюда при условии $x ⁄= 0,x⁄= −1,y ⁄= 0$ получаем

2 12-= -(x2-+1)-- 7 x − x+1

5x2− 26x+ 5= 0

Решая это квадратное уравнение, получаем $x= 5$ или $1 x = 5.$ Из первого равенства тогда $1 y = 5$ или $y = 25$ соответственно.

Подставляем получившиеся значения в требуемое выражение:

( ) ( ) (( ) ) 52⋅(52+ 1)⋅ 1 2 =26 и 1 2⋅ 1 2+ 1 ⋅252 =26 5 5 5

Ответ: 26

Ошибка.
Попробуйте повторить позже

Задача 11#49494

В классе $28$ учеников. На уроке программирования они делятся на три группы. На уроке английского языка они тоже делятся на три группы, но по-другому. И на уроке физкультуры они делятся на три группы каким-то третьим способом. Докажите, что найдутся хотя бы два ученика, которые на всех трёх занятиях находятся друг с другом в одной группе.

Источники: Турнир Ломоносова-2017, отборочный тур, (см. turlom.olimpiada.ru)

Подсказки к задаче

Подсказка 1

Давайте немного переформулируем задачу, чтобы условие стало проще, а Дирихле применить было легче! Посмотрим на одного ученика. В первый раз его распределили в одну из трех групп, потом еще раз в одну из трех других групп, и в третий раз снова в одну из трех групп. Занумеруем эти группы. Тогда каждому ученику сопоставим последовательность из трех номеров групп, в которых он оказался!

Подсказка 2

Например, Вася был сначала в первой группе, затем в третьей, а на физкультуре снова в первой. Тогда его последовательность - 1,3,1. Теперь наша задача доказать, что у каких-то двух учеников полностью совпали их последовательности! Тут нам и поможет принцип Дирихле

Показать доказательство

Первое решение.

На уроке программирования можно выбрать группу, в которой $10$ человек, по принципу Дирихле (если нужно посадить $28$ котиков в $3$ домика, то найдётся домик, в котором хотя бы $10$ котиков, иначе всего их не больше $3⋅9= 27 <28$ ). Рассмотрим эти десять ребят, которые уже провели один урок в одной группе. На уроке английского хотя бы $4$ из них снова будут в одной группе по принципу Дирихле (если садим $10$ кроликов в $3$ клетки, то хотя бы в одной клетке найдётся $4$ кролика). Теперь рассмотрим этих четверых детей и снова заметим, что по принципу Дирихле на уроке физкультуры найдутся двое в одной группе. Эти двое и являются искомыми учениками.

Второе решение.

На каждом из трёх предметов занумеруем группы числами от $1$ до $3.$ Каждому ученику сопоставим последовательность из трех номеров групп (в фиксированном порядке), в которых он оказался. Всего последовательностей длины $3,$ состоящих из чисел $1,2,3,$ ровно $3⋅3⋅3= 27< 28.$ Тогда по принципу Дирихле найдутся два ученика с одинаковыми последовательностями, это и означает, что на всех предметах они попали в одинаковые группы.

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#67200

В выпуклом четырёхугольнике две противоположные стороны равны и перпендикулярны, а две другие равны $a$ и $b.$ Найдите его площадь.

Источники: Турнир Ломоносова-2016, отборочный тур (см. turlom.olimpiada.ru)

Подсказки к задаче

Подсказка 1

Когда в задачах по геометрии даны перпендикулярные прямые, но явно не обозначена точка их пересечения, то часто бывает, что нужно продлить прямые до их пересечения. Попробуйте сделать это и в нашей задаче. Какие фигуры получатся?

Подсказка 2

Правильно, получатся два прямоугольных треугольника — с гипотенузой, равной а, и с гипотенузой, равной b. Обозначьте неизвестные стороны какими-нибудь буквами, не забывая, что перпендикулярные стороны равны друг другу. Как теперь выразить площадь четырехугольника?

Подсказка 3

Верно, как разницу площадей этих прямоугольных треугольников! Теперь у нас есть формула для площади, но в ней всё ещё присутствуют неизвестные стороны. Значит, нужно найти, как ещё данные a и b из условия связаны c длинами неизвестных сторон. Какую теорему о прямоугольных прямоугольниках мы знаем?

Подсказка 4

Теорему Пифагора! Распишите теорему Пифагора для прямоугольных треугольников, немного преобразуйте и подставьте в формулу для площади!

Показать ответ и решение

Если $a =b,$ то получаем прямоугольник, у которого противоположные стороны параллельны, а не перпендикулярны.

Пусть для определённости дальше $b> a.$ Если $a> b,$ то нужно будет в ответе поменять буквы местами, поэтому учтём это знаком модуля.

Первое решение.

$PIC$

Обозначим длину двух равных сторон через $x$ . Продолжим их до пересечения и обозначим длины двух получившихся коротких отрезков через $y$ и $z.$ Площадь $S$ исходного четырёхугольника есть разность площадей двух прямоугольных треугольников: с катетами $x +y$ и $x+ z$ и с катетами $y$ и $z$ . Поэтому

2S = (x+ y)(x+ z)− yz = x2+xy +xz

По теореме Пифагора

y2+ z2 =a2,(x +y)2+ (x+ z)2 =b2

Поэтому

2 2 2 b− a = 2x +2xy+ 2xz = 4

В итоге площадь многоугольника равна

b2− a2 4

Второе решение.

$PIC$

Из четырёх таких многоугольников можно сложить квадрат со стороной $b,$ из которого вырезан квадрат со стороной $a.$ Поэтому площадь одного многоугольника равна $14(b2 − a2).$

Ответ:

$1 ||b2− a2|| 4$

Ошибка.
Попробуйте повторить позже

Задача 13#49149

Все коэффициенты многочлена $P(x)$ — целые числа. Известно, что $P(1)= 1$ и что $P(n)= 0$ при некотором натуральном $n$ . Найдите $n.$

Источники: Турнир Ломоносова-2001, 10-11.5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Когда в задании фигурирует многочлен с целыми коэф-ами, а тем более два его значения, то Вам должна вспоминаться теорема Безу, которую и следует тут применить.

Подсказка 2

Р(n)-Р(1) делится на n-1, в то же время оно равно -1. Теперь остается вспомнить, что n - это натуральное число :)

Показать ответ и решение

Воспользуемся теоремой Безу