Ошибка.
Попробуйте повторить позже
Сколько точек пространства с целочисленными координатами принадлежат треугольнику с вершинами ,
,
? Точка
на вершинах и сторонах тоже считаются.
Источники:
Подсказка 1
Давайте немного упростим задачу и сдвинем одну из вершин в начало координат, чтобы числа стали попроще, для этого можно сделать параллельный перенос на вектор (-3;-4;-5), а как можно посчитать кол-во целочисленных точек на стороне?
Подсказка 2
Верно, кол-во целых точек (включая концы) на отрезке (x₁,y₁,z₁), (x₂,y₂,z₂), это НОД(|x₁-x₂|, |y₁-y₂|, |z₁-z₂|) + 1, итак, когда мы знаем кол-во точек на периметре треугольника, давайте перейдём к его внутренности, если взять произвольную целочисленную точку, можно ли получить какое-то следствие, которое было бы легче проверить, но оно бы оставило нам пару точек для перебора?
Подсказка 3
Да, можно сказать, что если точка A была подходящей, то точка A' полученная проецированием её на одну из плоскостей тоже будет подходить, а значит можно спроецировать весь треугольник, например, на плоскость Oxy и найти возможных кандидатов там, а потом проверить только их
Подсказка 4
Для проверки наших кандидатов можно составить систему уравнений из двух векторов, образующих стороны, с положительными коэффициентами, сумма которых меньше 1, чтобы получить точку внутри треугольника, остаётся проверить, что найдутся целые решения, которые бы удовлетворяли полученной системе
Подсказка 5
Для удобства можно выразить из первых двух уравнений коэффициенты и подставить их в третье уравнение, тогда останется лишь условие на координаты точек, но предыдущие ограничения всё ещё следует проверить
Перенесём треугольник одной вершиной в начало координат. Тогда его можно представлять как точку , из которой выходят вектора
и
.
Тогда внутренность треугольника можно представить как где
— действительные числа,
и
Вопрос о целых точках на треугольнике, получается, стоит так: при каких целых система:
имеет решения , удовлетворяющие условиям выше.
Мы выделили внутренность, потому что стороны легче рассмотреть отдельно. Три целочисленные вершины лежат в треугольнике по
определению. На сторонах точки подсчитать тоже просто — стороны это вектора и третья сторона
.
Получить целочисленную точку можно только на середине вектора
, а у остальных сторон нет общих делителей координат, и через целые
точки они не проходят. Значит, на периметре лежат
точки.
Переходим к внутренней части треугольника. Конечно, нет гарантий, что там будет хотя бы одна целочисленная точка —
но если такая есть, то её проекции на координатные плоскости тоже будут целочисленные. Поэтому давайте рассмотрим
проекцию треугольника на плоскость , и отберём на ней потенциально подходящие пары
а после выкинем
лишние.
Проецируем треугольник на — получается треугольник на плоскости с вершинами
Внутрь него точки попадут
такие:
Решаем систему, состоящую из двух первых уравнений:
Получаем следующие решения:
Полученные значения подставляются в третье уравнение
, и если
оказывается целым — точка найдена. После
подстановки получается выражение:
то есть должна быть чётной. Из
кандидатов подойдут только
.
Плюс точки на сторонах, и всего точек на треугольнике
Ошибка.
Попробуйте повторить позже
Пусть обозначает сумму цифр натурального числа
. Найдите наибольшее
-значное натуральное число
, удовлетворяющее
условию: для всех натуральных
(
) справедливы равенства
.
Источники:
Подсказка 1
Не совсем понятно, как нам искать максимальное подходящее число из 85значных чисел. Быть может, рассмотрим какие-нибудь большие числа и посмотрим, подходят ли они?
Подсказка 2
Докажем, что число 10^85 - 1 подходит. Посмотрим, что происходит при умножении на какое-то число, известно ли нам что-нибудь о его виде? О сумме цифр? Удобно рассматривать m без нулей на концах.
Подсказка 3
Что происходит, когда мы отнимаем от числа m * 10^85 число m? Удобнее всего рассмотреть вычитание столбиком.
Подсказка 4
У 86 -го разряда числа m * 10^85 занимается единица. Тогда у остальных младших 85 разрядов вместо 0 будет 9, кроме последнего, у которого будет 10. А что будет в ответе в этих разрядах? Какой будет сумма в этих разрядах?
Подсказка 5
Тогда сумма цифр до 86 -го разряда будет равняться 9*84 + 10 - S(m). Осталось лишь найти, чему будет равна сумма чисел в оставшихся разрядах!
Максимальное -значное натуральное число это
Докажем, что оно подходит под условие.
Если тогда
Сумма цифр у числа
равняется
Рассмотрим сумму цифр у
Будем
рассматривать такие
что они не оканчиваются на
так как нули не влияют на сумму цифр
Соответственно переходов через
разряд у
нет.
Когда из вычитается число
происходит следующее:
(a) У -го разряда числа
занимается единица. Тогда у остальных младших
разрядов вместо
будет
кроме
последнего, у которого будет
(b) При вычитании числа в результате будет в разрядах будет записываться такая цифра, что в сумме с цифрой из
стоящей на
том же разряде, они дадут
кроме первого разряда, у которого в сумме будет
Тогда сумма цифр до -го разряда будет равняться
так как изначально было девяток и одна десятка.
Оставшаяся сумма цифр числа будет равняться
Но учитывая ограничения, которые мы ввели, получаем, что
Тогда сумма цифр числа это
что совпадает со суммой цифр числа
Ошибка.
Попробуйте повторить позже
Старинный подземный ход имеет свод параболической формы (то есть в поперечном сечении туннель ограничен полом — осью и
графиком некоторой параболы
). Ширина туннеля (измеряется по полу) равна
, высота туннеля равна
. Ход укрепили
распорками — на параболе отметили точки
,
,
,
и соединили их между собой балками. Балки
и
параллельны полу,
пересекается с
, и при этом
. Найдите расстояние между балками
и
.
Источники:
Подсказка 1
Давайте введем на нашей картинке систему координат, которая была бы нам удобна. К примеру симметричную относительно прямой симметрии параболы и нулевой высоты в тоннеле. Тогда, что нужно чтобы зафиксировать картинку? Каких параметров будет достаточно, чтобы выразить через это всю картинку?
Подсказка 2
Нам достаточно h - высоты вершины, а также длины основания - 2l(для симметрии). Тогда, если наша парабола задается функцией f(x) = a - bx^2, то f(l) = f(-l), f(0) = h. Тогда f(x) = h(1 - x^2/l^2). Значит, мы можем задать две точки A и C, а остальные - будут отличаться от симметричных только умножением на -1 абсциссы. Давайте так и сделаем - пусть x_1 - абсцисса А, а x_2 - абсцисса C. Тогда как нам выразить перпендикулярность, если мы работаем в координатах? Мы ведь не использовали еще ни разу тот факт, что, к примеру, AC и CB перпендикулярны.
Подсказка 3
Верно, мы можем выразить это через скалярное произведение векторов AC и CB. После того, как мы запишем и преобразуем выражение, у нас получится, что -(x_2^2 - x_1^2) - (h^2)/(l^4) * (x_2^2 - x_1^2)^2 = 0. Но при этом, у нас x_1 != x_2, поэтому x_2^2 - x_1^2 = - (h^2)/(l^4). Тогда, нам остается понять, чему равно расстояние между балками и записать ответ!
Обозначим ширину тоннеля за , а высоту за
. Из этих параметров однозначно выводятся параметры параболы:
принадлежит
отрезку
а
так что
Теперь зададим координаты точек так:
Так как и
параллельны полу, то понятно, что ординаты
и
одинаковы. Значит, абсциссы отличаются только знаком.
Аналогично для
и
.
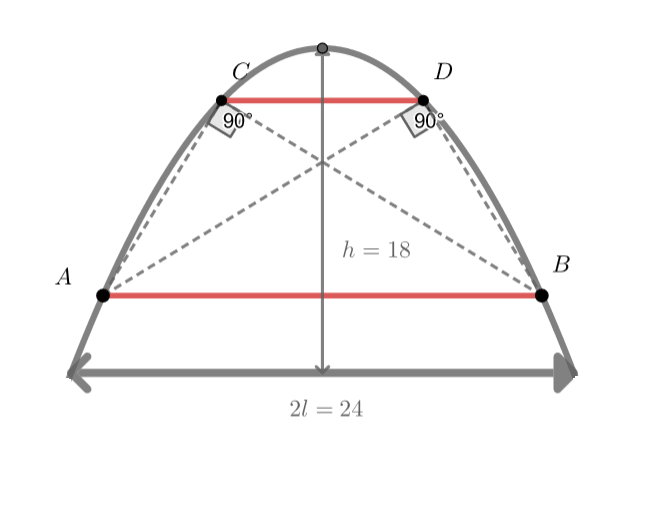
Тогда перпендикулярность и
и
можно выразить, например, через равенство нулю скалярных произведений.
Достаточно рассмотреть одну пару, так как рисунок симметричен.
Тогда либо (но балки не совпадают, поэтому такой вариант не подойдет), либо
А расстояние между балками это:
Ошибка.
Попробуйте повторить позже
Функция такова, что
Найдите тангенс угла наклона касательной к графику функции
в точке .
Источники:
Подсказка 1
В аргументе функции стоит сложное дробно-линейное выражение от х, из-за этого трудно понять, как выглядит сама функция. Но с другой стороны, мы же понимаем, что можно сделать замену в этом аргументе так, чтобы нам стало удобнее работать с функцией. На руку играет то, что и в аргументе, и в правой части выражения в знаменателе стоит (х+1), то есть эти два выражения довольно сильно похожи.
Подсказка 2
Если получилось воспользоваться предыдущей подсказкой, то функция должна принять вид линейной. А многократное применение линейной функции — совсем не проблема:)
Подсказка 3
Понятно, что тангенс угла наклона касательной — это значение производной в соответствующей точке. А когда мы берем производную от функции, слагаемое-константа исчезает, поэтому в процессе многократного применения нашей функции за константой можно даже не следить.
Преобразуем выражение аргумента
Выполним замену Тогда
, следовательно, для любого
верно, что
Тем самым, мы показали, что функция имеет вид
, где
— некоторая постоянная, которая не зависит от
,
тогда
следовательно, для некоторой новой постоянной
. Аналогично,
Осталось заметить, что тангенс угла наклона в точке 0 равен значению производной функции в точке 0, так что
Ошибка.
Попробуйте повторить позже
Автодром состоит из трех попарно касающихся кольцевых трасс (две окружности касаются друг друга попарно в точке внешним
образом и третьей в точках
и
внутренним, причём
— диаметр третьей окружности). Автомобиль в любой точке касания может
продолжать движение по любой из двух возможных трасс, но нигде не может разворачиваться на
. По каждой из трех трасс
автомобиль едет со своей скоростью, так что любую из двух
длиной
км он проезжает за
минут, любую из дуг
длиной
км — за
минут, а любую из дуг
— за
минут. Выехав из точки
, автомобиль через
час
минут оказался в ней же.
Сколько километров проехал автомобиль?
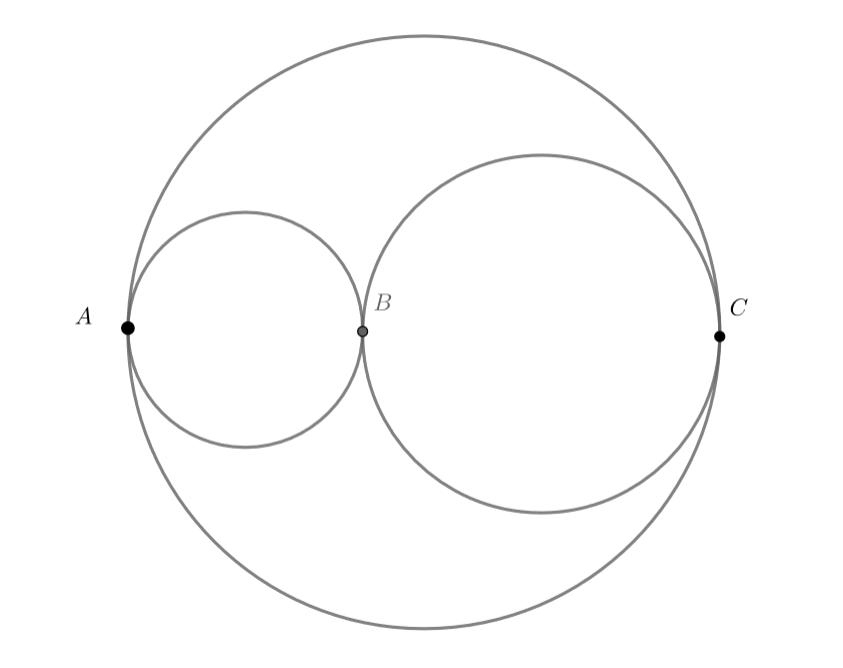
Источники:
Рассмотрим варианты, которыми находящийся в точке автомобиль может в следующий раз впервые снова оказаться в этой
точке.
Во-первых, можно сделать это, не проходя через точку , т. е. путем
.
Во-вторых, можно одним из двух способов ( или
) добраться до точки
, сделать несколько кругов
(«несколько»
может быть и нулем) и вернуться одним из двух способов (
или
) в точку
.
В любом случае мы либо четное число раз проезжаем по 7-минутной дуге, четное число раз по 11-минутной и четное число раз по 17 -минутной, либо наоборот, нечетное число раз по каждому из трех типов дуг.
То же самое можно сказать про неоднократное возвращение в точку .
«Четный» случай нам не подходит, так как по условию на каждую дугу уходит целое число минут, а общее время выражается в минутах
нечетным числом. Заметим, что любая тройка нечетных положительных чисел может быть реализована в качестве числа проходов (в любом
направлении) дуг ,
,
.
Действительно, выехав из точки и сделав заданное нечетное число проходов
, мы окажемся в точке
, после чего, сделав
заданное нечетное число проходов
, мы окажемся в точке
, а после заданного нечетного числа проходов
— снова в точке
.
Итак, попробуем найти три таких нечетных положительных числа ,
,
, что
Для возможны
варианта:
Первый случай отбрасываем, так как для него получаем
Во втором случае имеем . Если
, то
При
число
не делится на
.
Наконец, при имеем
. Для
получим
, откуда
а пройденный путь
равен
Здесь
— длина дуги
, которую находим геометрически:
где — радиусы.
Ошибка.
Попробуйте повторить позже
Решите систему уравнений
Источники:
Подсказка 1
Надо понять, какие есть возможности выполнения 1-го уравнения. Имеется одинаковая скобка справа и слева, на неё можно сократить (не забывая про модуль), когда она не равна нулю. Следовательно, можно отдельно рассмотреть случаи равенства и неравенства нулю этой скобки, также не забывая про ОДЗ.
Подсказка 2
Когда ни одна из скобок первого уравнения не равна нулю, учесть модули можно довольно просто — их наличие равносильно тому, что произведение всех скобок без модулей положительно (поскольку, если оставить все модули в одной стороне, а скобки без модулей перенести в другую, то дробь без модулей обязана быть положительной). Далее уже сложностей не остается — нужно лишь аккуратно поделить всё на случаи и довести их до конца, учитывая ОДЗ.
Из второго уравнения следует, что , так как корень неотрицателен.
Пусть первое уравнение выполняется из-за того, что . Условие равносильно
. Решение
не
подходит, а при
получаем:
Пусть теперь , но
, и
. Тогда
, но такой вариант не подходит под второе
уравнение.
При остальных система равносильна системе:
При решением будет
, при
получим уравнение:
Откуда , тогда
. Последняя пара не удовлетворяет условию
.
Ошибка.
Попробуйте повторить позже
Живописец закрасил акварелью полумесяц на клетчатой бумаге. Контур полумесяца состоит из двух дуг — одна от окружности с центром в
, проходящей через
, другая — от окружности с центром в
, проходящей через
. К утру краска расплылась так, что
каждая точка полумесяца превратилась в круг радиуса
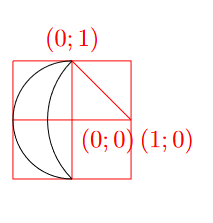
Найдите площадь получившейся фигуры.
Источники:
Подсказка 1
Когда краска расплылась, мы получили сложную фигуру, для площади которой точно не существует формулы. В таких случаях мы разбиваем фигуру на более простые, площади которых умеем вычислять.
Подсказка 2
Мы умеем находить площади окружностей, колец, секторов. Данная картинка удобно разбивается на эти фигуры или их части. При том, очевидно, что на концах нашего полумесяца нельзя брать целые окружности, потому что иначе усложняется вычисление площади остальной части фигуры. Подумайте, как можно, используя данные фигуры, разбить нашу?
Подсказка 3
Давайте разобьём фигуру на следующие части:
Пусть рисунок расплылся на радиус . К площади полумесяца прибавятся «поля», которые можно разбить на левое, правое и два
закругления на концах рогов.
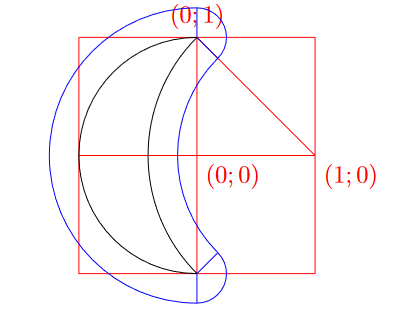
Площадь полумесяца равна половине площади круга радиуса минус сегмент круга радиуса
Площадь левого поля ”— половина от площади кольца с радиусами и
:
Площадь правого поля ”— четверть от площади кольца с радиусами и
:
Закругления на концах рогов вместе составляют три четверти окружности радиуса :
Вместе получается:
И тогда ответ:
Ошибка.
Попробуйте повторить позже
Болельщики должны выбрать 6 лучших хоккеистов чемпионата: одного вратаря, двух защитников и трех нападающих. Среди претендентов: 2 вратаря, 5 защитников, 6 нападающих и 3 “универсала”. “Универсал” — игрок, хороший в разных ролях, который поэтому может быть выбран как в качестве защитника, так и в качестве нападающего (но не вратаря). Сколько существует способов выбрать эту шестёрку? Требуется получить числовое значение.
Источники:
Подсказка 1
В задачах на комбинаторику всегда лучше начинать с простого и понятного. Кого в данной задаче можно выбрать без особых проблем?
Подсказка 2
Давайте сначала выберем вратаря, ведь место вратаря мажет занять только вратарь. Всего у нас два варианта на эту позицию. Обратите внимание, что защитников нужно выбрать только двое, и наша задача легко разбивается на три случая. Первый случай — это 0 универсалов среди защитников, второй — 1 универсал, третий — 2 универсала.
Подсказка 3
В каждом случае нужно из оставшихся игроков (нападающие + незадействованные универсалы) выбрать трех нападающих, число полученных вариантов для каждой позиции перемножить и результат сложить с остальными случаями.
Начнём считать с вратарей. Место вратаря может занять только вратарь, поэтому у нас всегда всего 2 способа выбрать его.
Дальше рассмотрим три случая по количеству универсалов на месте защитников:
1. Среди выбранных защитников нет универсалов. Значит, количество так выбрать двух защитников в команду равно
На место нападающих в этом случае мы можем поставить либо нападающих, либо универсалов, следовательно, способов
Следовательно, вариантов команд в этом случае
2. Среди выбранных защитников один универсал. Значит, количество так выбрать двух защитников в команду равно
На место нападающих в этом случае мы можем поставить либо нападающих, либо оставшихся универсалов, следовательно, способов
Следовательно, вариантов команд в этом случае
3. Среди выбранных защитников оба являются универсалами. Значит, количество так выбрать двух защитников в команду равно
На место нападающих в этом случае мы можем поставить либо нападающих, либо оставшегося универсала, следовательно, способов
Следовательно, вариантов команд в этом случае
В итоге способов выбрать команду равно
Ошибка.
Попробуйте повторить позже
Есть два ряда — верхний и нижний, каждый из 6 точек (см. рисунок). Проводят отрезки с концами в противоположных рядах так, чтобы из каждой точки выходил ровно один отрезок. Сколько существует способов провести отрезки, чтобы среди всех пар отрезков было ровно 7 пар пересекающихся отрезков?
Источники:
Подсказка 1
В таких задачах полезно посмотреть на случаи поменьше, с меньшим количеством отрезков и необходимых пересечений
Подсказка 2
Когда два отрезка пересекаются? Когда начало первого левее, чем начало второго, а конец первого правее, чем конец второго
Подсказка 3
Давайте посмотрим, что меняется, когда мы добавляем еще один отрезок.
Подсказка 4
Мы можем поставить второй конец в самую правую точку. Тогда у нас останется k пересечений.
Подсказка 5
Давайте подумаем, из каких расстановок отрезков для 5 пар точек мы можем получить необходимую расстановку для 6 пар точек.
Подсказка 6
Общая формула будет иметь вид
Пусть в каждом ряду по точек. Способ соединить точки можно задать перестановкой
чисел,
первая точка
верхнего ряда соединяется с точкой под номером
вторая — с
и так далее. Значит, всего возможных рисунков будет
Теперь берём пару отрезков. Пусть это отрезки с концами и
считаем
В каком случае они пересекается? В том, когда
Учитывая, что
могут быть любой парой, замечаем следующее: общее количество пересечений отрезков равно количеству
случаев, когда в перестановке большее число стоит раньше меньшего (не обязательно по соседству). Как сказали бы старшие товарищи,
число пересечений равно числу инверсий в перестановке. Так и будем говорить дальше.
Например, — нет инверсий и нет пересечений,
— одна инверсия (
и
—
инверсий (
и
и
и
и
и
и
Наибольшее количество инверсий будет, если написать числа задом наперёд:
какие два числа не выбери — большее будет стоять раньше. То есть инверсий в последнем примере
а в общем случае —
Как посчитать число перестановок с заданным количеством инверсий? Подойдём к задаче индуктивно. В фигурных скобках будем
указывать различные перестановки, а в квадратных перечислим количества перестановок, имеющих соответственно
инверсий.
Итак, единственный элемент можно расположить единственным образом, и у нас есть одна перестановка с нулевым числом инверсий.
Добавляем двойку — её можно добавить в начало и в конец имеющейся перестановки Одна из полученных перестановок будет без
инверсий, другая — с одной инверсией.
Добавляем тройку — её мы можем поставить в любое место каждой из имеющихся перестановок. Тройка больше всех имевшихся ранее чисел, поэтому если поставить её на последнее место — новых инверсий не добавится, если поставить на предпоследнее (на второе) — добавится одна инверсия, а если на первое — будет плюс две инверии. Одна перестановка с нулём инверсий, две перестановки с одной, две перестановки с двумя, одна перестановка с тремя. То есть:
Так же будет происходить добавление нового числа в общем случае: число
можно поставить на любое место, и в зависимости от
места к инверсиям добавится
штук. То есть на новом шаге перестановка с
инверсиями превращается в
перестановок с
инверсиями соответственно.
Посмотрим, какие числа получались в квадратных скобках. Напишем эти последовательности одну под другой:
Здесь в строке (нумерация начинается с
) приводятся числа
для
равные количеству перестановок из
чисел с
инверсиями.
Вспоминая, как происходит добавление нового получим
Действительно, — количество перестановок из (n-1) чисел, в которых уже есть
инверсий. В них мы вынуждены поставить новое
на последнее место (
инверсий). Раз мы ставим
на единственно возможное место, количество перестановок не
изменится.
Далее, — количество перестановок с
инверсией, и, чтобы добавить недостающую, мы вынуждены ставить
на
предпоследнее место (
инверсия).
Продолжаем так вплоть до потому что добавить больше
инверсии нельзя. Всего получается
слагаемых. Из других
перестановок предыдущей строки мы ничего нового получить не сможем.
Заметим, что так как не бывает перестановок с отрицательным числом инверсий, как и не может быть перестановок со
слишком большим (больше чем
) количеством инверсий.
Итак, имеем следующий способ построения коллекции
Первая строчка:
По строчке ползёт «окно» шириной Попавшие в «окно» числа складываются и выписываются в следующую (2-ю)
строку:
Вторая строка:
По ней будет ползти окно шириной Сложение попавших в окно чисел даст третью строку:
По ней поползёт окно шириной и так далее, чтобы получить
строку, нужно складывать
стоящих подряд чисел предыдущей
строки.
Выпишем (без нулей) первые строк нашей коллекции и выберем в ней нужное нам
Получаем ответ
Ошибка.
Попробуйте повторить позже
На подвешенном воздухе кубике Рубика, на одном из его квадратиков, сидит жучок. В какой-то момент он начинает
движение по поверхности куба, передвигаясь за каждую секунду на соседний квадратик, т.е. на квадратик, имеющий общую
сторону с текущим. Соседний квадратик для первого перемещения был выбран произвольно, а затем жучок следовал таким
правилам:
1) при 2-м, 4-м и других чётных перемещениях жучок не менял направления своего движения, т.е. покидал квадратик через сторону, противоположную той, через которую он на этот квадратик попал;
2) при 3-м, 5-м и других нечётных перемещениях жучок поворачивал направо (относительно своего движения).
Через 2023 секунды после начала движения жучок обратил внимание на то, что уже был на этом же квадратике 5 секунд назад. Через какое наименьшее число секунд после 2023-й жучок опять окажется на этом квадратике?
Источники:
Подсказка 1
Заметим, что квадратиков ну ооочень много, но ведь многие из них очень похожи?… Если взять конкретный квадратик, то несложно отследить его путь, т.к путь у жучка определяется начальным положением и направлением. Что тогда попробуем сделать?
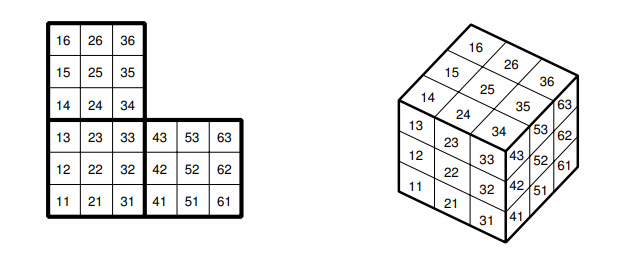
Для отслеживания движения жучка будем использовать частичную развертку куба, покрывающую грани. Каждый квадратик будем
обозначать двузначным числом, 1-я и 2-я цифры которого являются соответствующими координатами центра квадратика на развертке
(единица — ширина квадратика):
Маршрут жучка определяется его начальным положением и направлением его первого перемещения. Хотя всего таких вариантов
их все можно разбить на
принципиально различных групп:
1) Жучок стартует с центрального квадратика любой грани по направлению к любому ребру
2-3) Старт с углового квадратика любой грани, а первое перемещение в пределах той же грани вдоль ребра, идущего соответственно справа или слева от жучка
4-5) Старт с углового квадратика любой грани, а при первом перемещении жучок переползает на соседнюю грань, причем третья примыкающая грань остается соответственно справа или слева от него
6) Старт с приреберного квадратика любой грани по направлению к центру
7) Старт с приреберного квадратика любой грани с переходом на соседнюю грань при первом перемещении
8-9) Старт с приреберного квадратика любой грани, а первое перемещение в пределах той же грани вдоль ребра, идущего соответственно справа или слева от жучка
Заполним таблицу, в которой для каждой группы приведем пример маршрута в течение того времени, когда обнаруживается его
периодичность, т.е. когда на какой-либо четной секунде жучок оказывается на начальном квадратике, а еще через с — на квадратике, где
он был через
с после начала движения.
В случае группы выберем для старта квадратик
с первым перемещением
и проследим весь маршрут, пока не обнаружим,
что его период равен
c (1-я колонка таблицы после двойной вертикальной черты).
Заметим, что через c после начала движения жучок окажется в начальном состоянии группы
Поэтому для нее маршрут также
будет иметь период
с и его можно получить из маршрута группы
сдвигом на
с.
Еще через с жучок окажется в начальном состоянии группы
Поэтому и для нее маршрут будет с периодом
с и его можно
получить из маршрута группы
сдвигом на
с.
Еще через с имеем начальное состояние группы
и получаем ее маршрут с периодом
с из маршрута группы
сдвигом на
с.
Для остальных групп получаются кольцевые маршруты с периодом с, причем в течение одного периода жучок ни на одном
квадратике не оказывается дважды.
Так как (остаток от деления
на
равен
) и
(остаток от деления
на
равен
то через
с после начала движения жучок окажется на том же
квадратике, на котором он был через
с после начала, а за
с до этого — на том же квадратике, на котором он был через
с после
начала.
Как видно из таблицы, такое совпадение имеет место только для группы (квадратик
Так как этот квадратик встречается на
маршруте только дважды в течение периода (
с и
с), следующее попадание на него произойдет через
(с).
Ошибка.
Попробуйте повторить позже
Дана последовательность в которой
а отношение каждого следующего элемента к предыдущему при всех целых
равно
Найдите отношение 2023-го члена последовательности к сумме её первых 2022 членов.
Источники:
Подсказка 1
Напрямую искать это отношение не хочется. Давайте тогда начнем с aₙ, а там и придумаем. Вспомним, что у нас условие на отношение aₙ/aₙ₋₁. Как им хорошо можно воспользоваться?
Подсказка 2
А давайте перемножим эти условия для n, n-1, ..., 2, 1! Получится, что aₙ/a₁ = aₙ/aₙ₋₁ ⋅ aₙ₋₁}/aₙ₋₂} ⋅ ... ⋅ a₂/a₁ = (n²+1)n/((n-1)²+1) ⋅ ... ⋅ (2²+1)/(1+1) = (n²+1)⋅n!/2. У нас тут есть отношение aₙ к a₁, может тогда легче найти сумму/a₁, ведь отношение получившихся выражений как раз будет отношением aₙ/сумма? Давайте так и поступим)
Подсказка 3
Обозначим сумму первых n-1 члена за Sₙ₋₁. Даже зная aₙ/a₁ для любого n, не очень понятно, как хорошо свернуть сумму. А вдруг можно представить выражение (n²+1)⋅n!/2 как разность двух каких-то выражений, которые зависят от n и n-1? Например как какое-то bₙ - bₙ-₁. Тогда у нас выйдет, что Sₙ₋₁/a₁ будет bₙ₋-b₀, и зная эти b мы легко найдем то, что нам надо!
Подсказка 4
Пошаманим с aₙ/a₁: (n²+1)⋅n!/2 = 1/2 ⋅ (n(n+1) - (n-1)) ⋅ n! = n⋅(n+1)!/2 - (n-1)⋅n!/2. Вот как раз наши bшки! Обозначим тогда bₙ = n⋅(n+1)!/2. Остается найти сумму и посчитать отношение)
Найдем перемножив указанное в условии отношение для различных
Представим его в виде разности:
где
Тогда отношение суммы первых членов к
равно
Стало быть, ответ при равен
Ошибка.
Попробуйте повторить позже
Обозначим через число цифр в десятичной записи натурального числа
Найдите сумму
Источники:
Подсказка 1
Понятно, что количество цифр в числе n, это такое k, что 10ᵏ > n > 10ᵏ⁻¹. А какую еще знакомую нам функцию можно связать с k?
Подсказка 2
Логарифм! И правда, ведь получается, что k > log₁₀(n) > k-1. Тогда получается, что k = log₁₀(n) + a, где 0 < a < 1. Как теперь выражается искомая сумма?
Подсказка 3
Получается, что наша сумма это log₁₀(2²⁰²³) + log₁₀(5²⁰²³) + a+b = 2023 + a + b, где 0 < a+b < 2. Остается вспомнить, что количество цифр - это целое число, и станет понятно чему равно a+b!
Заметим, что
Аналогично,
Тогда
Значит, число целое, причем
так как
Отсюда
а ответ равен
Ошибка.
Попробуйте повторить позже
Две стороны выпуклого четырёхугольника имеют длину 6, ещё одна — длину 1, а его площадь — наибольшая возможная при таких условиях. Какова длина четвёртой стороны четырёхугольника?
Источники:
Подсказка 1
Пусть наши известные стороны это b, b и c, но мы не знаем, в каком порядке они расположены в четырехугольнике: как b, b, c или b, c, b? А вдруг это не важно?)
Подсказка 2
Пусть наш четырехугольник это ABCD, где AB = CD = b, BC = c. Тогда на самом деле площадь четырехугольника AB'CD, где AB' = c, B'C = CD = b будет такой же, потому что треугольник ACD не изменился, а ABC = AB'C, то есть площадь осталась такой же) Давайте теперь мыслить про первый вариант.
Подсказка 3
Можно ли отдельно максимизировать площадь, учитывая наши условия? Например, разбить четырехугольник на какие-то части, и меняя что либо, менять площадь?
Подсказка 4
Давайте отдельно максимизируем площадь ABC и ACD) Начнем с ABC. Мы знаем, что A находится на расстоянии b от точки B. Так давайте будет двигать A по окружности с центром в точке B и радиусом b! Сторона BC как раз не меняется в таком случае. В какой момент площадь ABC будет максимальна?
Подсказка 5
Тогда, когда AB станет перпендикулярна BC! Потому что площадь ABC = 1/2 ⋅ (высота к BC) ⋅ BC, и высота максимальна будет как раз в этом случае. Попробуйте сделать тоже самое с ACD) Какой четырехугольник в таком случае у нас выйдет?
Подсказка 6
Т.к. углы ABC и ADC станут по 90°, то ABCD - вписанный, да и еще у него AB = CD, то есть ABCD - равнобокая трапеция! Осталось посчитать сторону AD, зная все это)
Подсказка 7
Для удобства подсчета, стоит опустить высоты из B и C на AD и воспользоваться формулой высоты в прямоугольном треугольнике)
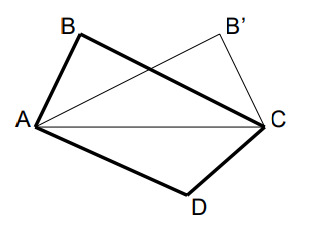
Пусть известные длины сторон четырехугольника равны и
В условии не указан порядок расположения этих сторон:
или
Но вместо четырехугольника
в котором, скажем
рассмотрим четырехугольник
в
котором,
В нем тот же набор известных длин сторон (но в другом порядке), а площади этих четырехугольников
равны, так как это суммы
и
причем
Поэтому можно считать, что
Заметим, что двигая точку по дуге окружности радиуса
с центром в точке
мы будем получать четырехугольник с тем же
набором известных длин сторон, с той же частью
а площадь части
будет наибольшей тогда, когда
(иначе при том
же основании
высота из точки
будет короче, чем
Двигая аналогично точку
вокруг точки
получим, что из свойства
максимальной площади четырехугольника
вытекает
Итак, имеются два прямоугольных треугольника и
с общей гипотенузой
и равными катетами
и
Значит,
треугольники равны, как и их высоты на гипотенузу, т.е.
— равнобедренная трапеция с тупыми углами
и
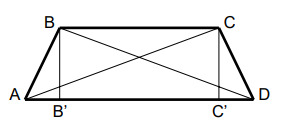
Пусть где
и
— проекции точек
и
на
Тогда из свойства высоты прямоугольного треугольника
получаем
Отсюда, с учётом того, что получаем
Подставляем и получаем
Ошибка.
Попробуйте повторить позже
Решите уравнение
Источники:
Подсказка 1
Выглядит страшно: и корни, и логарифм по отдельности..может, тут есть какие-то оценочки?)
Подсказка 2
Например, можно обратить внимание, что раз |x-2|³ ≥ 0, то аргумент логарифма ≥ 1, и сам логарифм ≥ 0. А еще в подкоренном выражении слева у старшего члена коэффициент больше, чем в подкоренном выражении справа. Что это может значить?
Подсказка 3
То, что левая часть почти всегда больше правой) А еще сами корни положительные. Поэтому, чтобы решение существовало, нужно чтобы левый корень был не больше, чем правый корень (т.к. логарифм и так ≥ 0). При каких иксах это так?
Подсказка 4
Если написать неравенство на подкоренные выражения, то после нехитрых преобразований, получится, что (x²-2)² ≤ 0! Т.е. x = ±√2. Проверьте, подходят ли они как решение)
Так как
Для существования решения необходимо, чтобы выполнялось неравенство
Проверка показывает, что — решение.
Ошибка.
Попробуйте повторить позже
При каком наименьшем по модулю значении параметра уравнение
имеет решение на отрезке
Источники:
Подсказка 1
Из-за страшного вида уравнения можно понять, что просто преобразованиями это не решить, значит тут какая-то идея! Вот интересное замечание: 1234+789 = 2023. На что это может натолкнуть?
Подсказка 2
Можно из этого понять, что т.к. синус и косинус по модулю не превосходят 1, то максимум левой части как раз равен 2023! Теперь можно приравнять синус к ±1, а косинус к -1, и посмотреть на корни.
Подсказка 3
Выходит системка вида x = 5π/6 + πk и ax = 5π/4 + 2πn. Давайте посмотрим, когда первый корень может быть в этом промежутке.
Подсказка 4
Да, только при k = -1, 0! Осталось разобраться с альфа. Давайте подставим первый корень во второй чтобы выразить альфа через n и k) Останется только понять, при каких n и k модуль этого выражения достигнет минимума, а зная чем может быть k, это не так сложно)
Так как синус и косинус по модулю не превосходят а
решением уравнения может быть только такой
при
котором входящие в уравнение синус и косинус равны соответственно
(при возведении в 20-ю степень даст
) и
(таким же
останется при возведении в 23-ю степень).
Подставив из первого выражение во второе, выразим
Найдём возможные целые значения подставив
в условие
Чтобы найти с наименьшим модулем, выберем
минимизирующее модуль числителя, (для приведенных числителей это
или
а также допустимое
максимизирующее модуль знаменателя. Нетрудно заметить, что это
и
поэтому
получаем
Ошибка.
Попробуйте повторить позже
Вычислите
где — это целая часть числа
(т.е. наибольшее целое число, не превосходящее
).
Источники:
Подсказка 1
Давайте обозначим наше выражение внутри скобок за t. Тут какие-то страшные корни, давайте избавимся от них с помощью возведения t в квадрат!
Подсказка 2
t² = 90 - 2√3. Стоит вспомнить, что 1 < √3 < 2, и, получив из этого оценку на t², легко найти целую часть от t!
Первое решение.
Обозначим Чтобы не возиться с корнями, попробуем оценить квадрат этого выражения, тем более он
довольно симпатичный:
Из очевидного получаем
. Откуда, конечно,
так что целая часть числа
равна
Здесь, однако, важно сказать, что
, иначе наше решение не исключало бы, что целая часть могла быть
равна
. Но в силу
следует очевидность (которую всё же надо упомянуть!) неравенства
Второе решение.
Когда мы видим такую разность корней, хочется немедленно домножить на сопряжённое (на сумму корней) и получить:
Далее остаётся оценить выражение в знаменателе. Покажем, что оно лежит строго от до
, тогда сама дробь лежит в интервале
и целая часть равна
. Итак,
, откуда
и
Поскольку , то остаётся показать, что
Отсюда
Ошибка.
Попробуйте повторить позже
Высота остроугольного треугольника
пересекается с его другими высотами в точке
Точка
лежит на отрезке
так,
что величина угла
максимальна. Найдите
если
Источники:
Подсказка 1
Чтобы найти наибольшую величину угла, попробуем искать наибольшее значение одной из тригонометрических функций этого угла. Какую будет использовать удобнее всего? В △BKH нет прямых углов, поэтому подумайте через какие углы лучше всего выразить ∠BKH?
Подсказка 2
tg(x-y) = (tg(x) - tg(y)) / 1 + tg(x) * tg(y). Заменив длину неизвестной стороны DK за x, получим функцию от x, максимум которой мы ищем
Подсказка 3
Производная функции обнуляется при x² = BD * BH. Как выразить это произведение через AD и DC?
Подсказка 4
tg(∠HAD) = ctg(∠BCD)
![]()
Чем больше острый угол, тем больше его тангенс. Поэтому условие максимальности угла можно заменить на условие
максимальности его тангенса. По формуле тангенса разности имеем
Максимум этого выражения достигается при том же значении , что и минимум выражения
где Производная
равна
и обращается в нуль при
(нас интересуют только положительные
значения
Заметим, что откуда
Таким образом,
Ошибка.
Попробуйте повторить позже
При каких значениях параметра наибольшее расстояние между корнями уравнения
принадлежащими интервалу принимает наименьшее значение? Найдите это наименьшее значение.
Источники:
Подсказка 1
Так, ну у нас тут кубическое уравнение относительно тангенса. В общем виде мы очень плохо решаем уравнения 3 степени, поэтому обычно в таких ситуациях мы пытаемся найти какое-то решение, а потом уже решать квадратное, поделив кубическое на это решение. Если вы верите в светлое будущее, то вам, скорее всего, нужно найти этот корень, потому как иначе непонятно, что делать и как исследовать разность между корнями, да ещё арктангенс брать. В общем, попытайтесь найти решение!
Подсказка 2
Ищется оно недолго, так как первая мысль «tgx = 1» срабатывает. После чего мы получим некоторый квадратный трехчлен, который уже можно разложить, либо просто угадав корни, либо через дискриминант. Получим, итого, (t - 1)(t - a)(at + 2) = 0, где t = tgx. Посмотрим на корни t = а и t = -2/a(если a!=0). Что можно про них сказать?
Подсказка 3
В силу того, что tgх нечетная функция, выходит, что один из корней точно < 0(уже после взятия арктангенса). Но при этом у нас есть корень pi/4. Что тогда можно сказать про наибольшее расстояние? А если а = 0?
Подсказка 4
Верно, что оно больше pi/4. Но в этих случаях, мы рассмотрели ситуации, когда a!=0, так как иначе один из корней не определен. Если же а = 0 , то есть два корня - 0 и pi/4. И тут расстояние ровно pi/4. Значит, в других ситуациях расстояние больше pi/4, а в этом pi/4. Значит, есть и оценка, и пример!
Данное уравнение можно переписать в виде
Откуда при либо
и
либо
и
либо (при
и
Таким
образом, данное уравнение имеет на интервале
два или три различных корня (второй корень не может совпадать с третьим, так
как
и
имеют разные знаки при любом
в силу нечётности арктангенса).
Случай 1: Тогда остаётся два корня
и
которые отличаются на
Случай 2: Тогда разность между корнями
и
больше, чем
Случай 3: Тогда разность между корнями
и
больше, чем
при
Ошибка.
Попробуйте повторить позже
Если действительные числа упорядочить по нестрогому возрастанию, получив тройку
то число
будем называться
средним из чисел
Найдите все значения
при каждом из которых среднее из трёх чисел
положительно.
Источники:
Подсказка 1
Среднее из трёх чисел положительно, а числа заданы с параметром да еще и в виде функций... Сравнивать такие числа реально сложно, надо подумать, как можно переформулировать вопрос.
Подсказка 2
Если рассуждать в общем, то для того, чтобы среднее из трех чисел было положительно, среди них должно быть не менее двух положительных, иначе условие задачи не выполниться (два числа будут неположительными, а среднее по нестрогому возрастанию уж точно!)
Подсказка 3
То есть нам подойдут случаи, когда два или три числа положительны. Теперь поймем, когда же наши числа будут положительными = найдем нули функций и отметим их на вещественной прямой.
Подсказка 4
Сначала можно отметить нули чисел(функций) a и b, так как кол-во их нулей конечно, расставить знаки функций на каждом промежутке и заметить, что некоторые промежутки нам уже подходят, а некоторые - точно нет.
Подсказка 5
Осталось понять знаки числа(функции) с, это можно сделать только на уже потенциально подходящих нам промежутках, выписать их объединение в ответ.
Напрямую значения сравнивать сложно. Однако, чтобы среднее из трёх чисел было положительным, необходимо и достаточно, чтобы
по крайней мере два числа из тройки были положительны.
Нужно, чтобы хотя бы два из трех чисел были положительны. и
при
область
идёт в ответ.
и
при
эта область в ответе быть не может. На оставшейся области
положительно только
одно из чисел
Значит, в ответ пойдут те её части, где
Посмотрим, как пересекаются
При получим интервал
Он с областью
не пересекается, ведь
При получим интервал
Он лежит в области целиком, ведь
Интервал идёт в
ответ.
При получим интервал
Он тоже лежит в области целиком, ведь
Интервал идёт в ответ.
При получим интервал
Тут получается такое неравенство:
интервал пересекается с областью
пересечение - это множество
которое пойдёт в
ответ.
При остальных интервалы заведомо лежат либо далеко левее
либо правее
и на ответ не повлияют.
В итоге ответ складывается из объединения множеств
Ошибка.
Попробуйте повторить позже
Угол при вершине в осевом сечении конуса равен . Снаружи этого конуса расположены 11 шаров радиуса 3, каждый из
которых касается двух соседних шаров, боковой поверхности конуса и плоскости его основания. Найдите радиус основания
конуса.
Источники:
Подсказка 1
Давайте сначала рассмотрим расположение любого шара и конуса в плоскости, перпендикулярной рисунку.
Подсказка 2
У нас есть треугольник, которого касается окружность известного радиуса, вписанная во внешний угол при основании треугольника. Счёт за Вами... Напоминаем, окружность, вписанная в угол, лежит на его биссектрисе
Подсказка 3
Теперь давайте поймем как расположены все шары снаружи. Они касаются друг друга, поверхности конуса и плоскости его основания, причем все расположены на одинаковом расстоянии от центра основания конуса!
Подсказка 4
То есть точки касания шаров с плоскостью основания конуса являются вершина правильного 11-угольника со стороной, равной удвоенному радиусу шаров(так как они касаются друг друга и длина = 2 радиуса)...
Подсказка 5
Теперь нам известны расстояние от центра основания до точки касания шаров с плоскостью основания(радиус 11-угольника) и расстояние от этой точки касания до ближайшей вершины треугольника в плоскости рисунка, тогда искомый радиус основания = радиус 11-угольника - последнее расстояние
![]()
Пусть — центр окружности основания конуса, радиуса
- центр одного из шаров радиуса
— точка касания этого шара с
плоскостью основания,
— точка касания соседнего шара с плоскостью основания конуса. Значит, из треугольника
можем
получить
![]()
Так как каждый шар касается двух соседних, то точки касания этих шаров с плоскостью основания конуса расположены в вершинах
правильного 11-угольника вписанного в окружность с центром в точке радиуса
и стороной, равной
Поэтому



