Мы имеем уравнение следующего типа:

Следовательно, наше уравнение преобразуется следующим образом:

Будем рассматривать параметр как переменную. Построим в системе координат множество решений системы. Если некоторая точка плоскости с координатами принадлежит этому множеству то для исходной задачи это означает, что если параметр принимает значение то будет одним из решений системы. Нас просят найти все такие значения параметра при каждом из которых ровно четыре точки вида , где принадлежат множеству решений изображенному на плоскости Фактически это равносильно тому, что горизонтальная прямая имеет ровно четыре точки пересечения с множеством

Неравенство системы задает множество точек плоскости находящихся не ниже прямой Первое и второе уравнения совокупности задают две окружности.

Первое — окружность с центром в точке радиуса

Второе — окружность с центром в точке радиуса

Заметим, что обе окружности проходят через начало координат, так как в уравнениях совокупности отсутствуют свободные члены. Следовательно, если подставить и уравнения будут верными равенствами.

Тогда — первая точка пересечения окружностей и прямой

Найдем вторую точку пересечения каждой окружности с этой прямой.

Для первой окружности и прямой получаем систему:

Для второй окружности и прямой получаем систему:

Следовательно, вторая точка пересечения первой окружности с прямой совпадает со второй точкой пересечения второй окружности с прямой. Назовем эту точку

Следовательно, получаем рисунки ниже (на рис. 2 приближено пересечение прямой с окружностями).

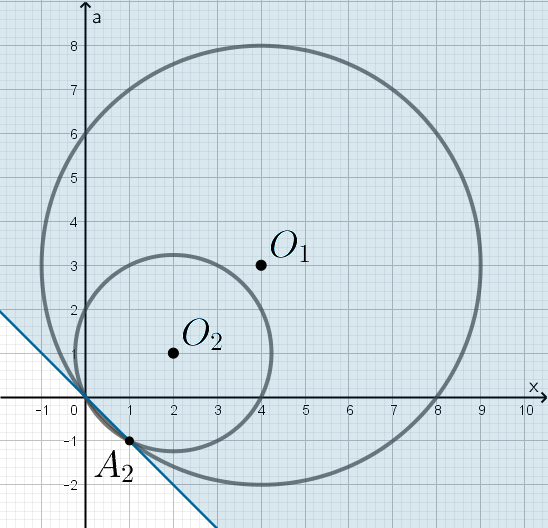
Рис. 1

     

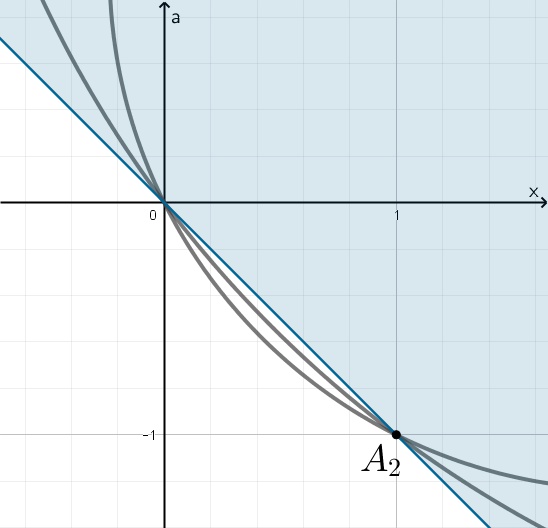
Рис. 2

Следовательно, части окружностей, находящиеся между их точками пересечения, не лежат в области Таким образом, множество решений системы, а значит и исходного уравнения, на плоскости выглядит следующим образом:

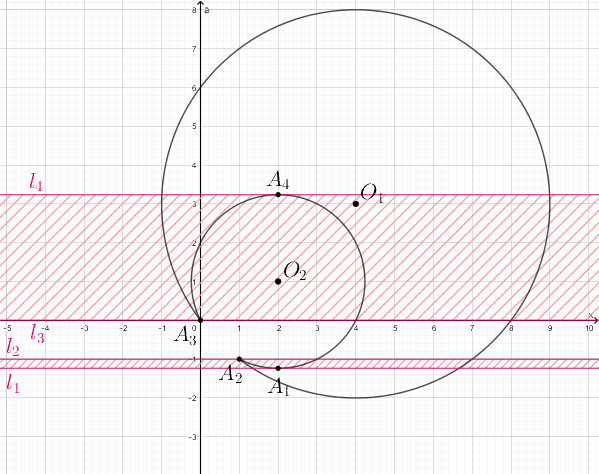
Закрашенные области (между прямыми и и , но не включая эти прямые!) — это те области, в которых может располагаться прямая чтобы иметь четыре точки пересечения со множеством Каждая — горизонтальная прямая, проходящая через

1.

Ордината точки ищется как разность ординаты центра окружности и радиуса этой окружности, то есть эта ордината равна Следовательно, уравнение прямой

2.

Ордината точки равна -1, следовательно, уравнение

3.

Точка — начало координат, следовательно, уравнение

4.

Ордината ищется как сумма ординаты центра окружности и ее радиуса, следовательно, эта ордината равна Значит, уравнение

Таким образом, подходящие значения параметра: