Сделаем замену , . Тогда уравнение примет вид

Будем постепенно выписывать условия, при которых исходное уравнение будет иметь шесть решений.
Заметим, что квадратное уравнение может максимум иметь два решения. Любое кубическое уравнение может иметь не более трех решений. Следовательно, если уравнение имеет два различных решения (положительных!, так как должно быть больше нуля) и , то, сделав обратную замену, мы получим: Так как любое положительное число можно представить как в какой-то степени, например, , то первое уравнение совокупности перепишется в виде Как мы уже говорили, любое кубическое уравнение имеет не более трех решений, следовательно, каждое уравнение из совокупности будет иметь не более трех решений. А значит и вся совокупность будет иметь не более шести решений.
Значит, чтобы исходное уравнение имело шесть решений, квадратное уравнение должно иметь два различных решения, а каждое полученное кубическое уравнение (из совокупности) должно иметь три различных решения (причем ни одно решение одного уравнения не должно совпадать с каким-либо решением второго!)
Очевидно, что если квадратное уравнение будет иметь одно решение, то мы никак не получим шесть решений у исходного уравнения.

 

Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.

 

1) Чтобы уравнение имело два различных решения, его дискриминант должен быть положительным:

2) Также нужно, чтобы оба корня были положительными (так как ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно:

Таким образом, мы уже обеспечили себе два различных положительных корня и .

 

3) Давайте посмотрим на такое уравнение

При каких оно будет иметь три различных решения?
Рассмотрим функцию .
Можно разложить на множители: Следовательно, ее нули: .
Если найти производную , то мы получим две точки экстремума .
Следовательно, график выглядит так:

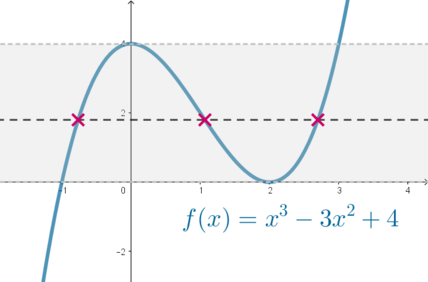
Мы видим, что любая горизонтальная прямая , где , пересекает график в трех точках. При всех остальных значениях будет меньше трех точек пересечения. Следовательно, для того, чтобы уравнение имело три различных решения, нужно, чтобы .
Таким образом, нужно: Давайте также сразу заметим, что если числа и различны, то и числа и будут различны, значит, и уравнения и будут иметь несовпадающие между собой корни.
Систему можно переписать так:

Таким образом, мы определили, что оба корня уравнения должны лежать в интервале . Как записать это условие?
В явном виде выписывать корни мы не будем.
Рассмотрим функцию . Ее график – парабола с ветвями вверх, которая имеет две точки пересечения с осью абсцисс (это условие мы записали в пункте 1)). Как должен выглядеть ее график, чтобы точки пересечения с осью абсцисс были в интервале ? Так:

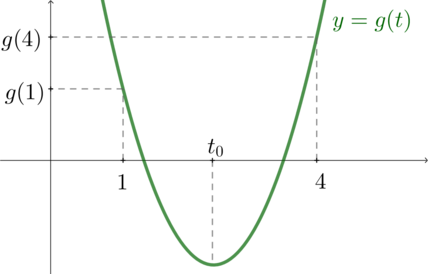
Во-первых, значения и функции в точках и должны быть положительными, во-вторых, вершина параболы должна также находиться в интервале . Следовательно, можно записать систему:

Таким образом, нам нужно пересечь значения параметра , найденные в 1-ом, 2-ом и 3-ем пунктах, и мы получим ответ: